Social Distance Swimming Pool

Question: It’s 8:59 at the $N$-lane town pool and the coronavirus is absolutely ripping. In an effort to mitigate the spread, swimmers must stay at least one lane apart. In one minute, the swimmers will hop into the pool, one lane at a time, until it becomes impossible to obey social distancing. If there are $N$ swimmers, how many do you expect to be left crying on the side of the pool?

(FiveThirtyEight)

Solution

The easiest way to get started on this problem is to get started on this problem. But let’s start simple, with $6$ lanes.

Suppose the first swimmer jumps in and she goes into the third lane. By the social distancing rule, this means that no other swimmer can go into the second lane or the fourth lane. We effectively now have two copies of the original problem playing out in lane $1$ and in lanes $5$ through $6$.

In other words, the total number of swimmers we expect, given that the first swimmer hopped into lane $3$ is the swimmer in lane $3$ plus the expected number of swimmers in a $1$ lane pool plus the expected number of swimmers in a $2$ lane pool.

If the first swimmer had instead gone into the second lane, we’d get

Since there’s an equal chance of the first swimmer going in any lane, the expected number of swimmers in the pool is

Diagramatically, we can picture this recursion like

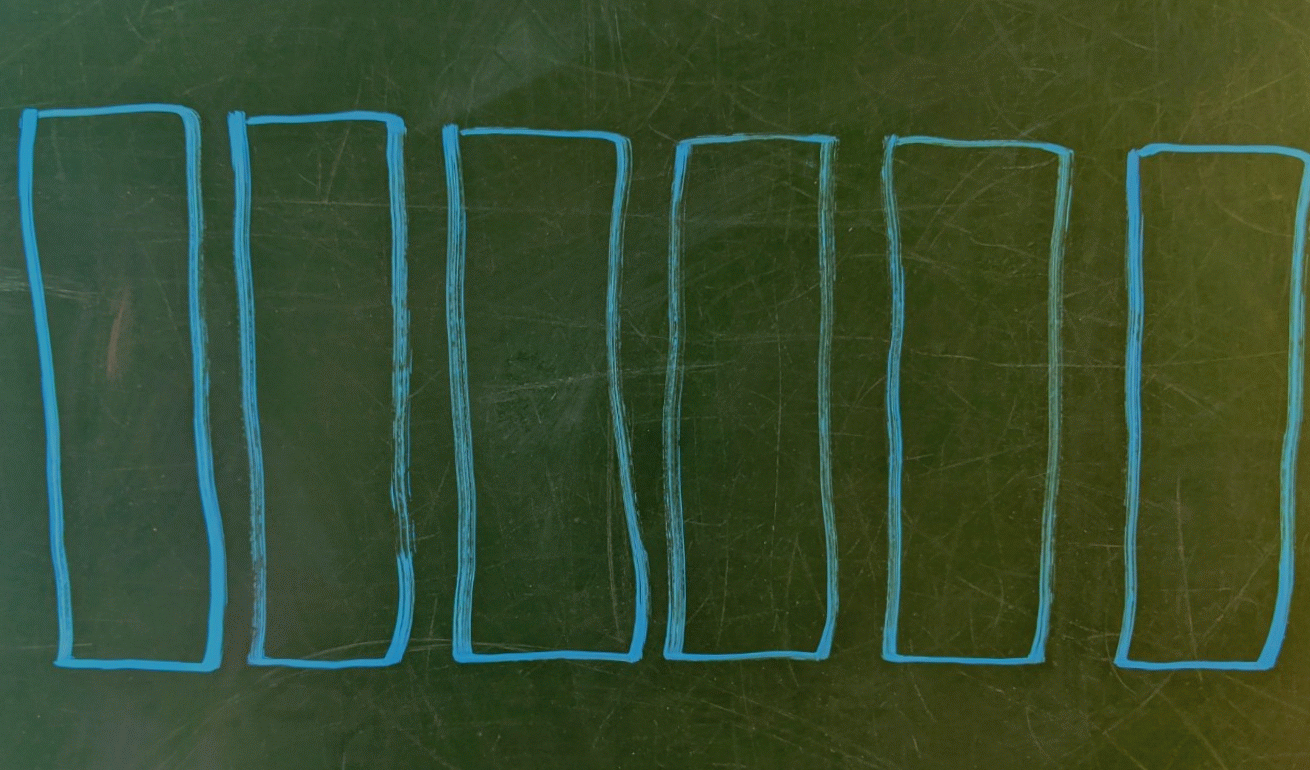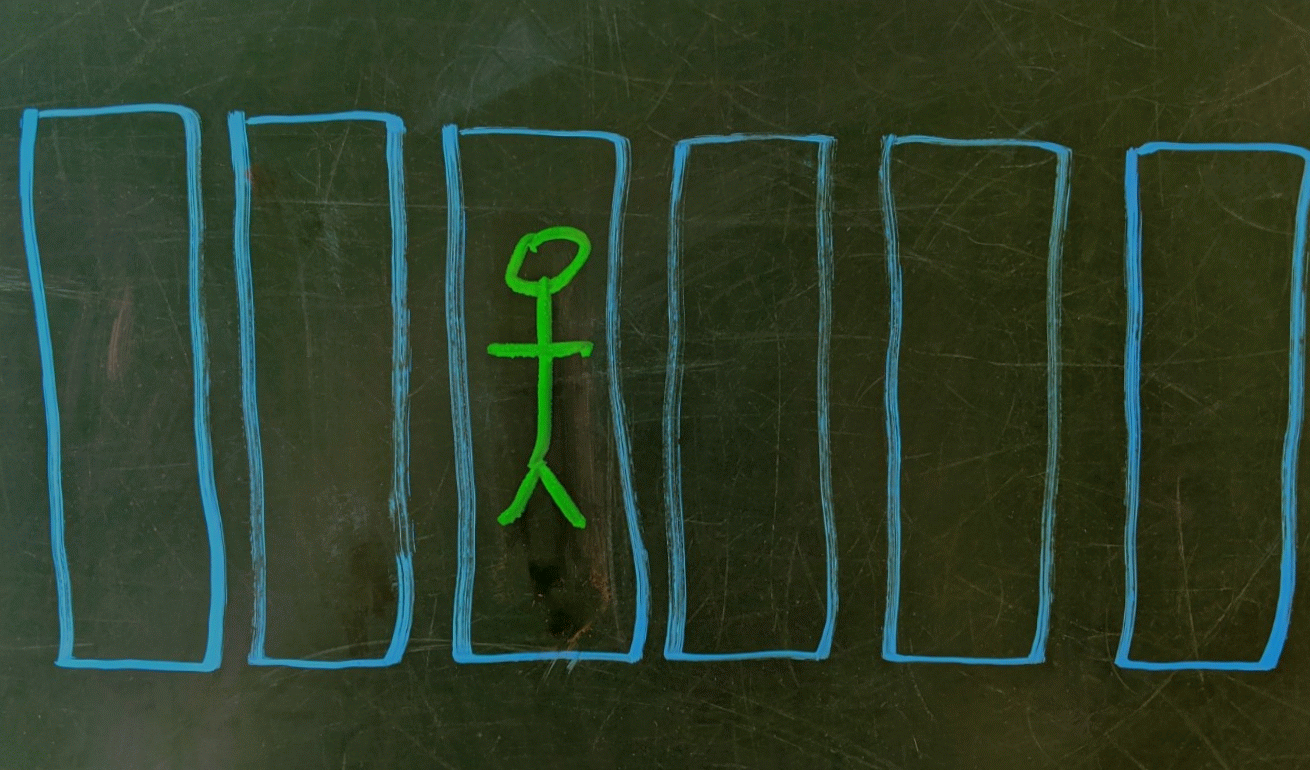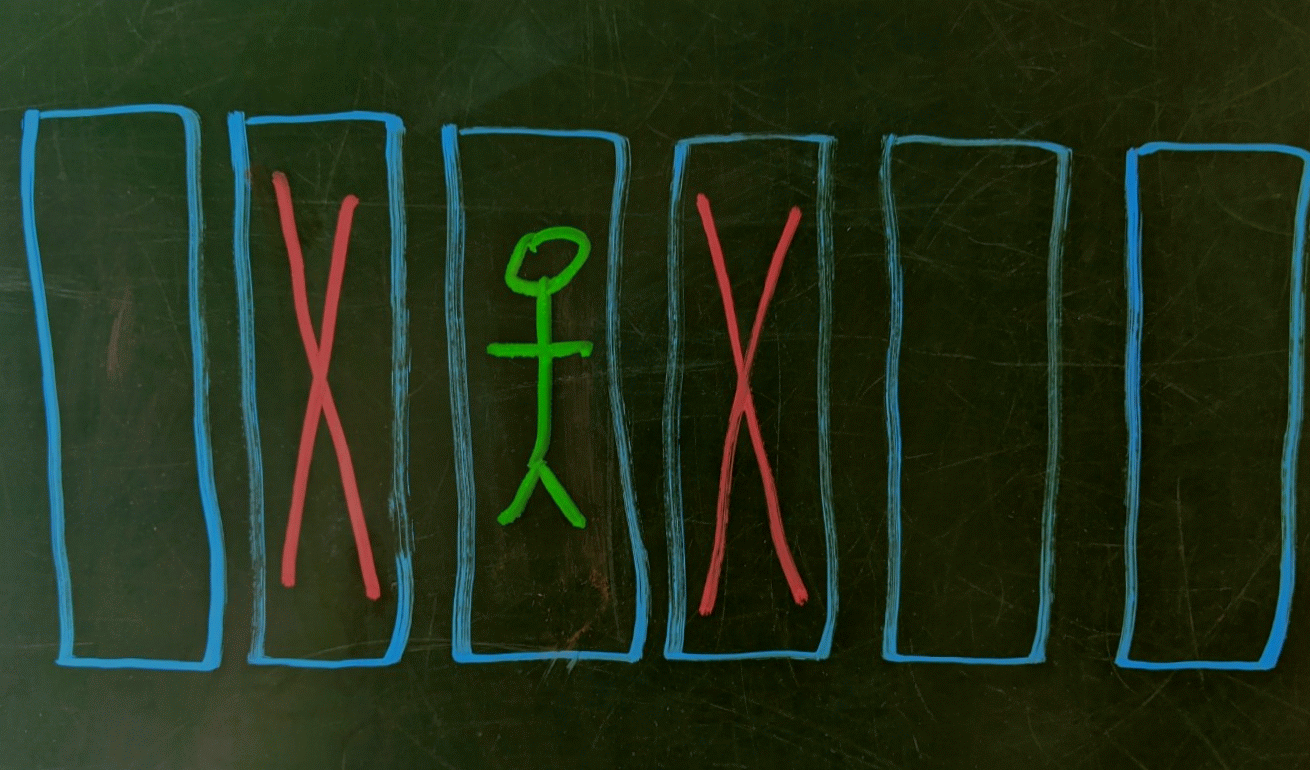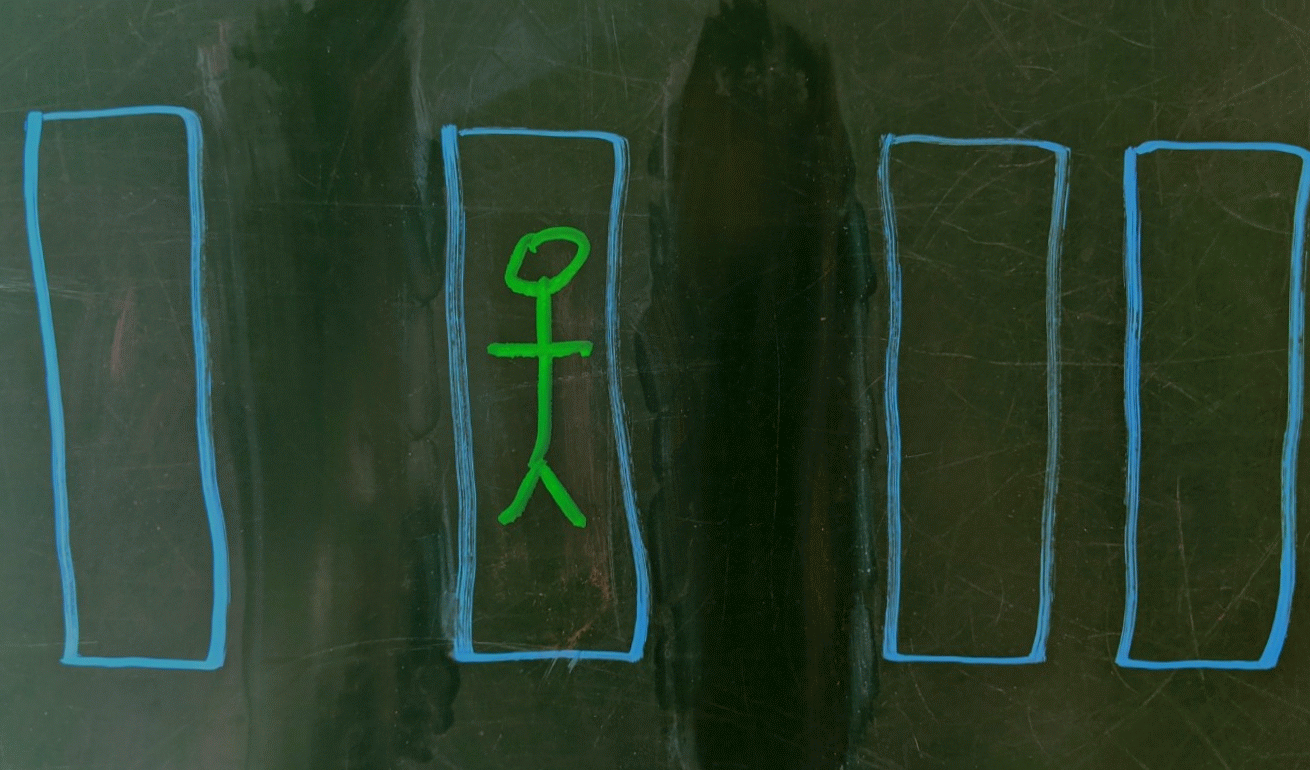
Illustrating the pool recursion induced by the first swimmer hopping in the third lane.

Generalizing, this becomes the recursive equation

So… how many swimmers?

Before moving on to finer points, let’s use the formula to find the expected number of swimmers in a $5$ lane pool. First of all, we have the base cases of $1$ and $2$ lane pools, for which we can only fit a single swimmer so $S(1) = S(2) = 1.$

For $5$ lanes, we get

plugging in $S(3) = 1 + 2S(1)/3 = 5/3$ and the bases cases, we get

So, on average, $5 - 37/15 \approx 2.53$ swimmers willl be left crying on the side of the pool.

Recursive evaluation

We can code this up (in Python) like

from functools import lru_cache

@lru_cache(maxsize=10_000)
def S(n):
    if n <= 2:
        return 1
    else:
        return 1 + 2 / n * sum( S(i) for i in range(1, n-1) )

Calculating S(5) we get $2.4\bar{6}$ in agreement with the calculation of $37/15$. Taking it to the next level, we find crushing linearity.

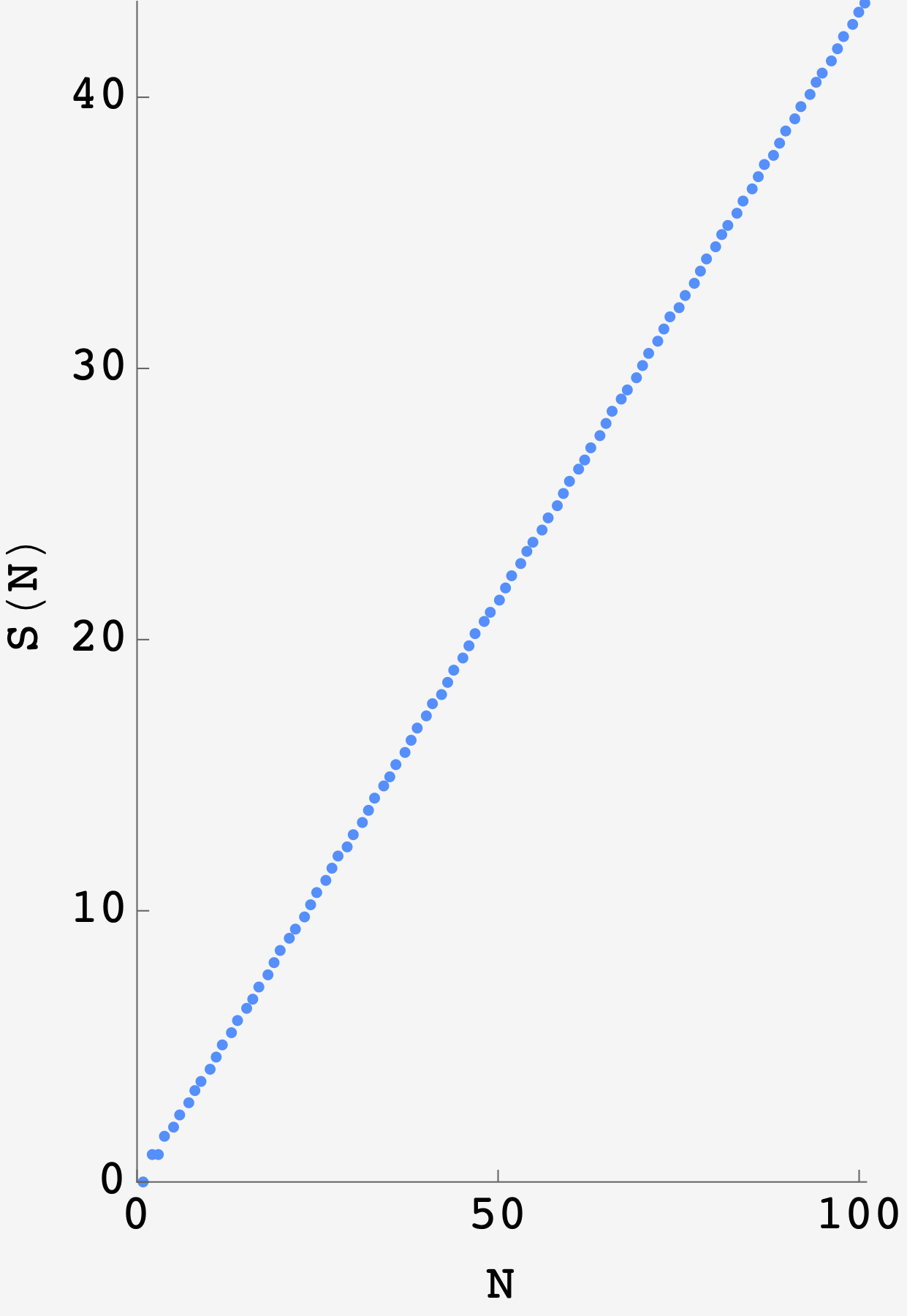
After the initial values, this thing gets very linear.

For reference, here are the first few coefficients:

What’s that slope?

With the numbers from the script, we could divide the rise of the line by its run and get a slope. But what is its closed form?

The simple truth is that we don’t deserve to know, not yet at least. We haven’t put in the work.

To go about it, I will return to the generating function, last employed in a similar capacity to how we’ll use it here: providing rigorous justification for an answer that we basically already had.

The basic idea (and miracle) is that it is easier to solve for the object $G = \sum S(n)x^n$ than it is to solve for $S(n)$ directly. Once we have $G$ we can Taylor expand and the coefficient on $x^n$, noted $\left[x^n\right]G,$ will be equal to $S(n).$

For a gentler introduction on how to use them, here’s my guide.

Starting from

we want to get $G(x) = \sum_n S(n)x^n.$ Going line by line,

which is enough to start working.

The column of bare powers of $x$ becomes $x/(1-x).$

Grouping terms,

Recognizing the term by term integrals,

The series inside the integral is just the generating function $G(x)$ so we get

This can be solved with integrating factors.

The left side looks like the derivative of $G(x)\times e^\text{(some function of $x$)}$ where the derivative of $\text{(some function of $x$)}$ is $-2x/(1-x)$:

So $\text{(some function of $x$)} = -\int dx\ 2x/(1-x) = 2x + 2\log(x-1)$ and $e^\text{(some function of $x$)} = e^{2x}\left(1-x\right)^2$.

By the series definition, $G(0)$ should be zero, so $C = -\frac12$ and

Remember, the whole idea is that the series expansion of $G(x)$ will have the $S(n)$ as its coefficients. Doing this, we get

which matches what we got with the script.

At last, we can go for the coefficient on $x^n$, $S(n).$ The numerator and denominator expand to

So the terms in the expansion have the form

Since we’re looking for the coefficient on $x^n,$ we can set $j + k = n$ so that becomes $\left(-2\right)^{k-1}(n-k+1)/k!$ and we sum over all possible $k$, so

working in the limit where $n$ is large, we can pull the $(n-k+1)$ out in front

which shows, at last, that the slope of the graph is $\left(1-e^{-2}\right)/2 \approx 0.43233235838169365$ As a check, we calculate S(100) - S(99) = 0.4323323583816858..., not bad.