Question: A post can accumulate spam comments, and each spam comment can accumulate spam comments. If each open reply thread accumulates spam at a rate of $1$ reply per day, then what is the expected number of spam posts by the end of a three day weekend?
Solution
Intuitive solution
In light of the nested spam threads, when I first thought about this I braced for keeping track of subprocesses of subprocesses of subprocesses. But as it turns out, all spam posts are the same in the eyes of the lord, and we only have to keep track of one top-level timeline.
The crucial insight is that new spam messages can spawn with equal opportunity in reply to any existing spam message. This means that whenever a new spam message is born the spam rate increases by 1 unit, $\lambda(S) = \left(1+S\right)\text{ spam / day}.$
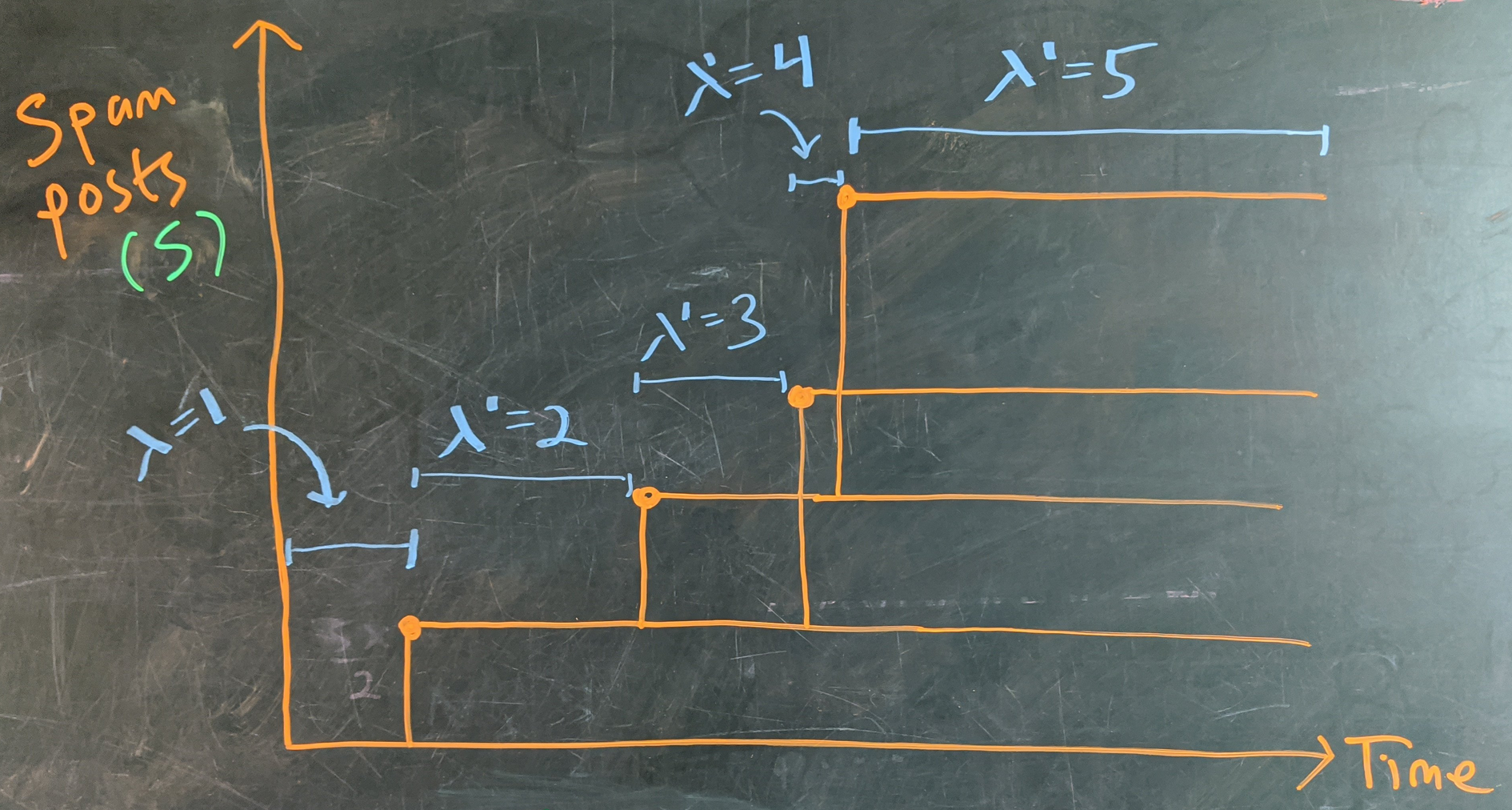
In other words, it’s an exponential growth process: each timeline exists to make copies of itself, which we can see with a bit of cartoon calculation:
By definition, the rate of change of spam posts per day is (averaging over all timelines)
\[\dot{S} = \lambda(S) = S + 1\]which, given that there are no spam posts to begin with, leads to
\[S = e^{\lambda t} - 1.\]Rigorous solution
Writing out the rate of change for the first few probabilities
\[\begin{align} \dot{p}_0 &= -\lambda p_0\\ \dot{p}_1 &= \lambda \left(p_0 - 2p_1\right)\\ \dot{p}_2 &= \lambda \left(2p_1 - 3p_2\right) \\ \dot{p}_3 &= \lambda \left(3p_2 - 4p_3\right) \end{align}\]shows that the rate equation has the general form $\dot{p}_n = \lambda\left(np_{n-1} - (n+1)p_n\right)$
(note that the linearity and pseudo-telescoping nature of these terms is what justifies the intuitive solution above)
Cleaning up using the step operator,
\[\dot{p}_n = \lambda\left(\mathbb{E}^{-1}-1\right)\left(n+1\right)p_n\]Solving all these coupled equations is a mess, so we try to get the generating function, $G(t,z) = \sum_n p_nz^n,$ which can be used to generate all sorts of things, like the mean
\[\langle S(t)\rangle = \partial_z G(t,z)|_{z=1}.\]Multiplying $\dot{p}_n$ by $z^n$ and summing over $n$:
\[\begin{align} \dot{G} &= \sum_n z^n \dot{p}_n \\ &= \lambda\sum_n z^n\left(\mathbb{E}^{-1}-1\right)(n+1)p_n \\ &= \lambda\sum_n (n+1)p_n \left(\mathbb{E}-1\right) z^n \\ &= \lambda\sum_n (n+1)p_n \left(z^{n+1}-z^n\right) \\ &= \lambda \left(z-1\right)\sum_n (n+1)p_n z^n \\ &= \lambda \left(z-1\right)\left(G + z\dfrac{\partial G}{\partial z}\right) \end{align}\](we used a fun-to-derive property of the step operator: $\sum_n f(n)\mathbb{E}g(n) = \sum_n g(n)\mathbb{E}^{-1}f(n)$)
This differential equation
\[\dfrac{\partial G}{\partial t} = \lambda (z-1)G + \lambda z(z-1)\dfrac{\partial G}{\partial z}\]can be solved with your favorite method, which might be the method of characteristics, to get
\[\boxed{G(t,z) = \dfrac{1}{z + (1-z)e^{t\lambda}}}.\]Mean
Upon taking $\partial_z G(t,z),$ gives the mean $\boxed{\langle S\rangle = e^{t\lambda} - 1}.$
Plugging in $\lambda =$ 1 post per day and $t=$ 3 days we get an expectation of $e^3 - 1 \approx 19.08$ posts by day $3.$
Slight changes in the spawn rate $\lambda$ produce massive increases in the weekend spam haul:
\[\begin{array}{c|c} \lambda & \langle\textbf{spam}(\text{3 days})\rangle\\ \hline 1 & 19 \\ 2 & 402 \\ 3 & 8102 \\ 4 & 162754 \\ 5 & 3269016 \\ 6 & 65659968 \\ 7 & 1318815733 \\ 8 & 26489122129 \\ 9 & 532048240601 \\ 10 & 10686474581523 \\ 11 & 214643579785915 \\ 12 & 4311231547115193 \end{array}\]Variance
We might expect the spawn of spam to be a bursty process (it could take a long while for the first spam, or a short while, and early gains can compound later gains). That can be found from $G(t,z)$ through
\[\langle \text{var } S(t)\rangle = \partial_z^2 G(t,z) + \partial_z G(t,z) - \left(\partial_z G(t,z)\right)^2 = e^{t\lambda}\left(e^{t\lambda}-1\right).\]Bursty indeed!
Median
The generating function $G(t,z)$ is a swiss-army knife and can be massaged to give the cumulative distribution function with little trouble. Inspecting its general form, can you see how to do this?
\[G(t,z) = p_0 + p_1z + p_2z^2 + p_3z^3 + \ldots\]We want the coefficient on, e.g., $z^3$ to end up as $p_0 + p_1 + p_2 + p_3$. We can do this by multiplying every term in the series by $1+z+z^2+z^3+\ldots$
\[\dfrac{G(t,z)}{1-z} = p_0 + (p_0+p_1)z + (p_0+p_1+p_2)z^2 + (p_0+p_1+p_2+p_3)z^3\ldots\]So, to get the $\text{cdf}$ we can just expand $G(t,z)/(z-1)$. Dividing $G(t,z)$ by $(1-z)$ gives a product of quotients that can be separated like
\[\dfrac{G(t,z))}{1-z} = \dfrac{1}{1-z} + \dfrac{1 - e^{-\lambda t}}{e^{-\lambda t}}\dfrac{1}{1-(1-e^{-\lambda t})z}\]Expanding both terms and isolating the coefficient on $z^s$, we get
\[\text{cdf}(s) = G(t,z)[z^s] = 1 - (1-e^{-t\lambda})^{s+1}\]Keep in mind: while the form of the coefficients is consistent for every term in the series, each term represent the cumulative probability of discrete quantities. We can use this function to solve for the median number of spam posts, but we’ll have to apply the ceiling function to account for the discrete outcomes:
\[\frac12 = 1 - (1-e^{-t\lambda})^{S_\text{median}+1}\]yields
\[\boxed{S_\text{median} = \Biggl\lceil -\left(\dfrac{1}{\log_2\left(1-e^{-3}\right)} + 1\right)\Biggr\rceil = 13\text { spam posts}}\]