Question: You’re playing a game of pinball that includes four lanes, each of which is initially unlit. Every time you flip the pinball, it passes through exactly one of the four lanes (chosen at random) and toggles that lane’s state. So if that lane is unlit, it becomes lit after the ball passes through. But if the lane is lit, it becomes unlit after the ball passes through.
On average, how many times will you have to flip the pinball until all four lanes are lit?
Extra credit: Instead of four lanes, now suppose your pinball game has $N$ lanes. And let’s say that $T_N$ represents the average number of pinball flips it takes until all $N$ lanes are lit up.
Now, each time you increase the number of lanes by one, you find that it takes you approximately twice as long to light up all the lanes. In other words, $T_{N+1}$ seems to be about double $T_N.$
But upon closer examination, you find that it’s not quite double. Moreover, there’s a particular value of N where the ratio $T_{N+1}/T_N$ is at a minimum. What is this value of $N$?
Solution
Let’s think about the pinball machine as a series of states corresponding to the number of lit lights:
\[\text{none} \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow \ldots \longleftrightarrow \text{all}.\]Each time we shoot a ball, we move from state to state. If there are $j$ lights turned on, then we have probability $j/N$ to move down, and probability $(1-j/N)$ to move up.
Bypassing the explicit probability distribution, we can relate the expected waiting time from state $j$ to the expected waiting time from states $(j-1)$ and state $(j+1)$:
\[\begin{align} T_j &= \dfrac{j}{N}\left(1 + T_{j-1}\right) + \left(1-\dfrac{j}{N}\right)\left(1+T_{j+1}\right) \\ &= 1 + \dfrac{j}{N}T_{j-1} + \left(1-\dfrac{j}{N}\right)T_{j+1} \end{align}\]By construction, this reflects the impossibility for state $j=0$ to move down (to $j=-1$) or for state $j=N$ to move up. Also, by definition, $T_N = 0,$ since all the lights are lit.
We can solve the system of equations for each value of $N$ and plot the ratio of consecutive waiting times as a function of $j:$
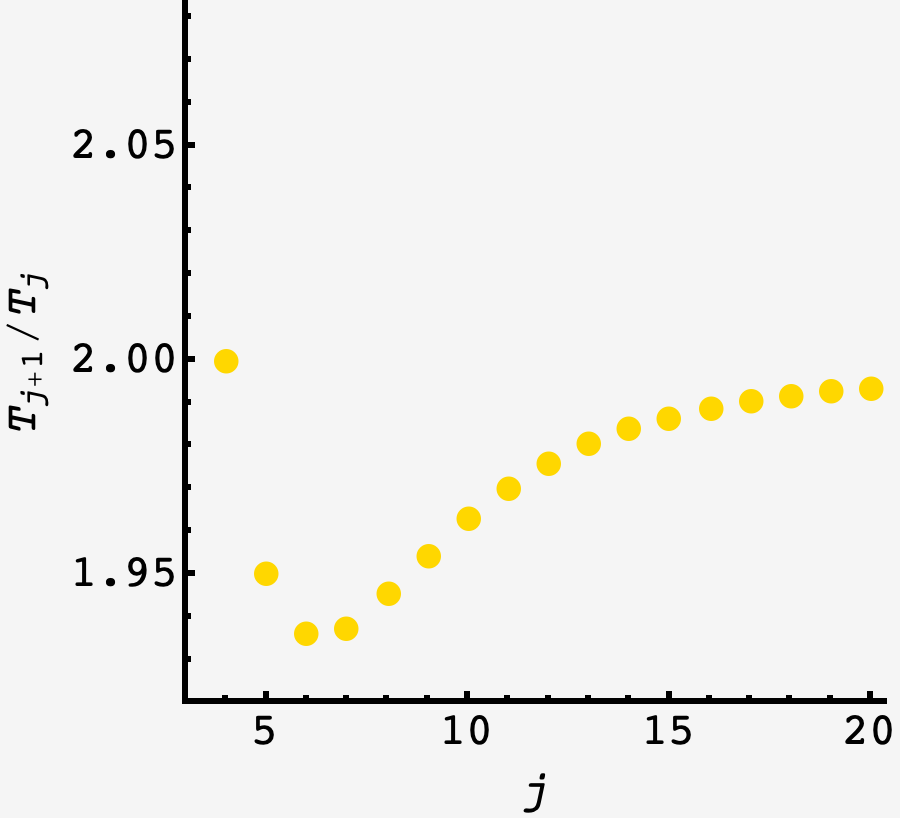
Evidently, the ratio is minimized at $j=6$ where
\[\dfrac{T_7}{T_6} = \frac{151}{78},\]which is about $2.5\%$ under the asymptotic value $2.$
makeEq[j_, NN_] := (
T[j] == 1 + j/NN T[j - 1] + (1 - j/NN) T[j + 1]
)
solveSystem[NN_] := (
(* make equations, set T[NN] to zero *)
eqns = Table[makeEq[j, NN], {j, 0, NN - 1}] /. {T[NN] -> 0};
(* solve the system *)
sol = Solve[eqns, Table[T[i], {i, 0, NN - 1}]];
(* return *)
Return[First[T[0] /. sol]]
)