Question: In the Great Riddlerian Desert, there is a single oasis that is straight and narrow. There are $n$ travelers who are trapped at the oasis, and one day, they agree that they will all leave. They independently pick a random location in the oasis from which to start and a random direction in which to travel. Once their supplies are packed, they all head out.
What is the probability that none of their paths will intersect, in terms of $n$? (For the purposes of this puzzle, assume the oasis is a line segment, while the desert is an infinite Cartesian plane.)
Solution
The basic idea is that two travelers won’t intersect so long as the one on the right makes a clockwise angle with the one on the left.
To start, we can go quick and dirty to get an idea of how the probability should scale.
Approximate argument
As $n$ gets big, about half the travelers will be on the top or bottom. Dividing the angular real estate into equal sized chunks, the travelers on the top can be afforded $1/(\frac12 n)$ of the available angles on the average. The same goes for the travelers on the bottom.
So, the probability of no intersections is approximately $P(n) \approx 1/(\frac12 n)^n = 2^n/n^n$ and, up to rescalings, we get $P(n) \sim n^{-n}.$
This shows the approximate $n$ dependence, but has the wrong scaling factor. Happily, the exact probability falls to a simple counting argument.
Counting argument
Really, the angle choices aren’t so restricted — the travelers can pick whatever angles they like and, as long as they’re in clockwise order, there won’t be any intersections.
To start, assume that the travelers pick their place on the line in some order.
Because every traveler starts from the oasis line, nobody from the up side can possibly intersect with anybody from the down side. So, we just need both sides to be correctly sorted. If there are $t_\text{up}$ travelers on the up side, and $t_\text{down}$ on the down side, then the probability that each side is correctly sorted is $1/(t_\text{up}!\cdot t_\text{down}!).$
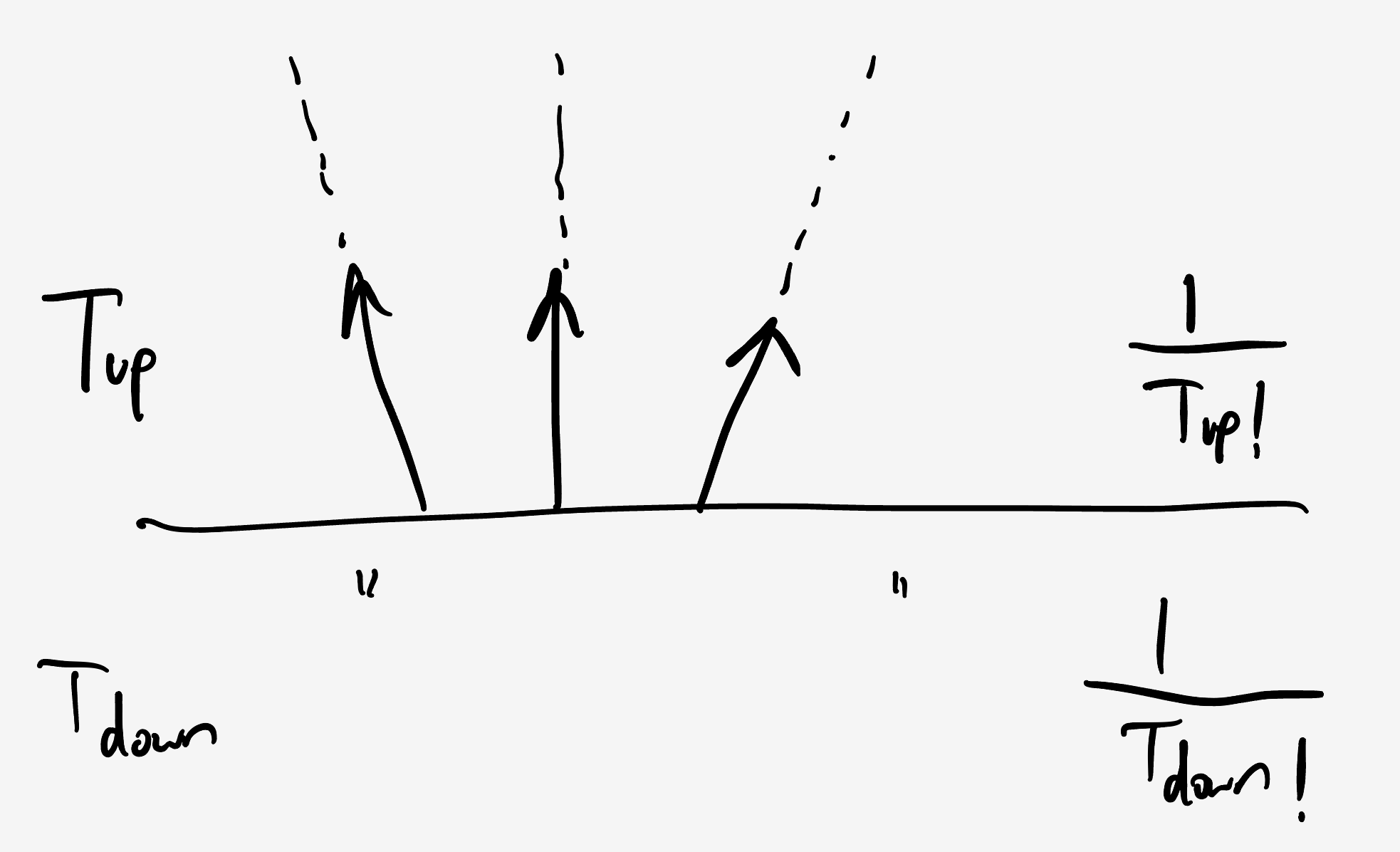
Going down the line, each traveler had even odds to point up or down, so the probability of any particular set of choices is $1/2^{t_\text{up}+t_\text{bottom}}.$ Also, we only care about the total number of up and down pointed travelers, not who they happen to be. Coarse graining, there are $\binom{t_\text{up} + t_\text{down}}{t_\text{up}}$ equivalent ways to pick $t_\text{up}$ up pointers and $t_\text{down}$ down pointers.
So, the chance of no intersections with a particular choice of $t_\text{up}$ and $t_\text{down}$ is
\[\frac{1}{2^{t_\text{up}+t_\text{down}}}\sum \binom{t_\text{up}+t_\text{down}}{t_\text{up}} \frac{1}{t_\text{up}!}\frac{1}{t_\text{down}!}\]Obviously, $t_\text{up}$ and $t_\text{down}$ add up to $n$: $t_\text{up} + t_\text{down} = n$ so, putting it all together, we get
\[P(n) = \frac{1}{2^n}\sum_{t_\text{up} = 0}^n \binom{n}{t_\text{up}} \frac{1}{t_\text{up}!}\frac{1}{(n - t_\text{up})!}\]We can clean this up with a bit of massaging.
If we multiply the top and bottom by $n!,$ then we get a sum of squares of the binomial coefficient $\sum \binom{n}{t_\text{up}}^2.$
Binomial coefficients are generated by the expansion of $(1+x)^n$ where the coefficient of $x^t$ is $\binom{n}{t}.$ Keeping in mind that $\binom{n}{t} = \binom{n}{n-t},$ if we zipper up the coefficients of $x^1$ with $x^{n-1},$ $x^2$ with $x^{n-2}$ and so on, then we get the sum of squared binomial coefficients.
So, if we multiply $(1+x)^n$ with itself, these binomial squares accumulate on the resulting $x^n$ term. However, $(1+x)^n(1+x)^n$ is the same as $(1+x)^{2n},$ whose $x^n$ coefficient is just $\binom{2n}{n}.$
So, the sum amounts to $\binom{2n}{n},$ and our overall probability is
\[\boxed{P(n) = \frac{1}{2^n n!}\binom{2n}{n}}\]Notably, up to scaling factors, this decays like $1/n^n.$