Grasshopper jumps

Question: You are trying to catch a grasshopper on a balance beam that is 1 meter long. Every time you try to catch it, it jumps to a random point along the interval between 20 centimeters left of its current position and 20 centimeters right of its current position.

If the grasshopper is within 20 centimeters of one of the edges, it will not jump off the edge. For example, if it is 10 centimeters from the left edge of the beam, then it will randomly jump to anywhere within 30 centimeters of that edge with equal probability (meaning it will be twice as likely to jump right as it is to jump left).

After many, many failed attempts to catch the grasshopper, where is it most likely to be on the beam? Where is it least likely? And what is the ratio between these respective probabilities?

(FiveThirtyEight)

Solution

To make this problem more concrete, we can think about many independent grasshoppers jumping around. Put them on the beam and then let them go. The relative fraction of grasshoppers at position $x$ in this situation is equal to $P(x)$ in the single grasshopper problem.

Lights, cameras, … time-reversal equality

After a long time has gone by, the grasshoppers will reach the equilibrium state where their probability distribution isn’t changing anymore.

Now, set up your camera and take a video of the grasshoppers jumping. If you play this movie forward and backward, you won’t be able to tell the difference, since the equilibrium probability distribution is constant in time. This means that the probability to observe any transition is the same as the probability to observe the reverse transition:

This is a tie that binds — between any two points on the beam, there is a perfect balance of forward and backward grasshopper transitions.

We can break this down with the help of Reverend Bayes — the probability to observe a grasshopper jump from $a\rightarrow b$ is the probability of being at $a$ times the probability of transitioning to $b$ given a start at $a:$

So, the time-reversal equality becomes

Wherefore art thou grasshoppers?

We can use the time-reversal equality to trace out the distribution over the entire balance beam.

The center

To start, compare two points $x$ and $y,$ both between $\tfrac15$ and $\tfrac45.$ Both can jump the full $\tfrac15$ to the left and $\tfrac15$ to the right, so $P(x\rightarrow y\rvert x)$ and $P(y\rightarrow x\rvert y)$ are uniform probability distributions over regions of width $\frac15 + \frac15 = \frac25,$ and $P(y\rightarrow x\rvert y) / P(x\rightarrow y\rvert x) = \frac25 \frac52 = 1.$

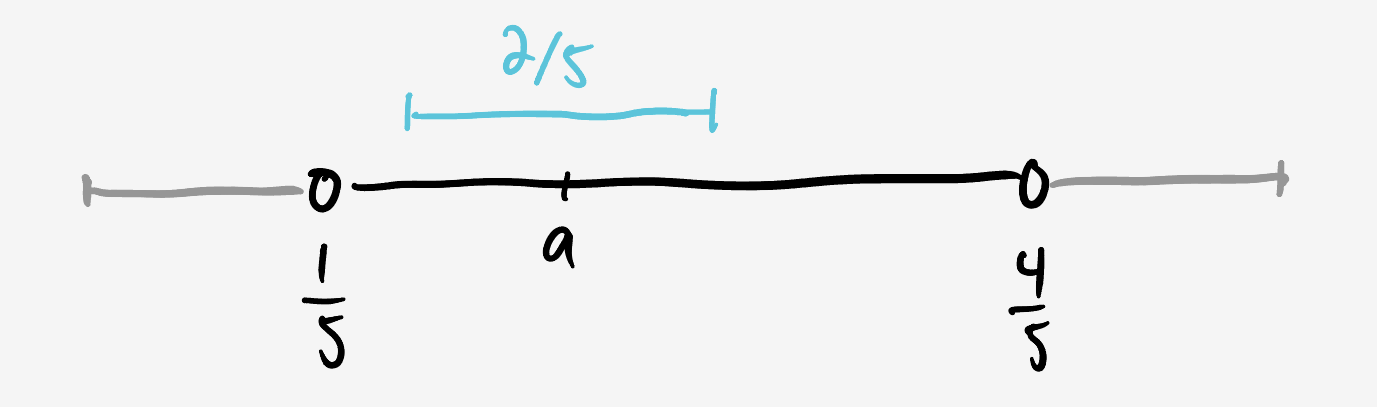
This means that $P(x) = P(y)$ for all such pairs of points and so $P(x) = \text{const.}$ in the region between $\frac15$ and $\frac45.$

The wings

Next, we can push into the wings by using $x=\frac15$ as an anchor point to investigate a point $y$ between $0$ and $\frac15.$

From $y,$ the grasshopper can jump a distance $y$ to the left, and $\tfrac15$ to the right, so $P(y\rightarrow x\rvert y)$ is a uniform distribution over a region of width $y + \frac15.$ Applying the time-reversal equality, we get

With this, we have the basic shape of the probability distribution: it starts at $\frac12\text{const.},$ then grows linearly to $\text{const.}$ at $x=\frac15,$ then stays flat until $x=\frac45,$ at which point it shrinks linearly back down to $\frac12\text{const.}$

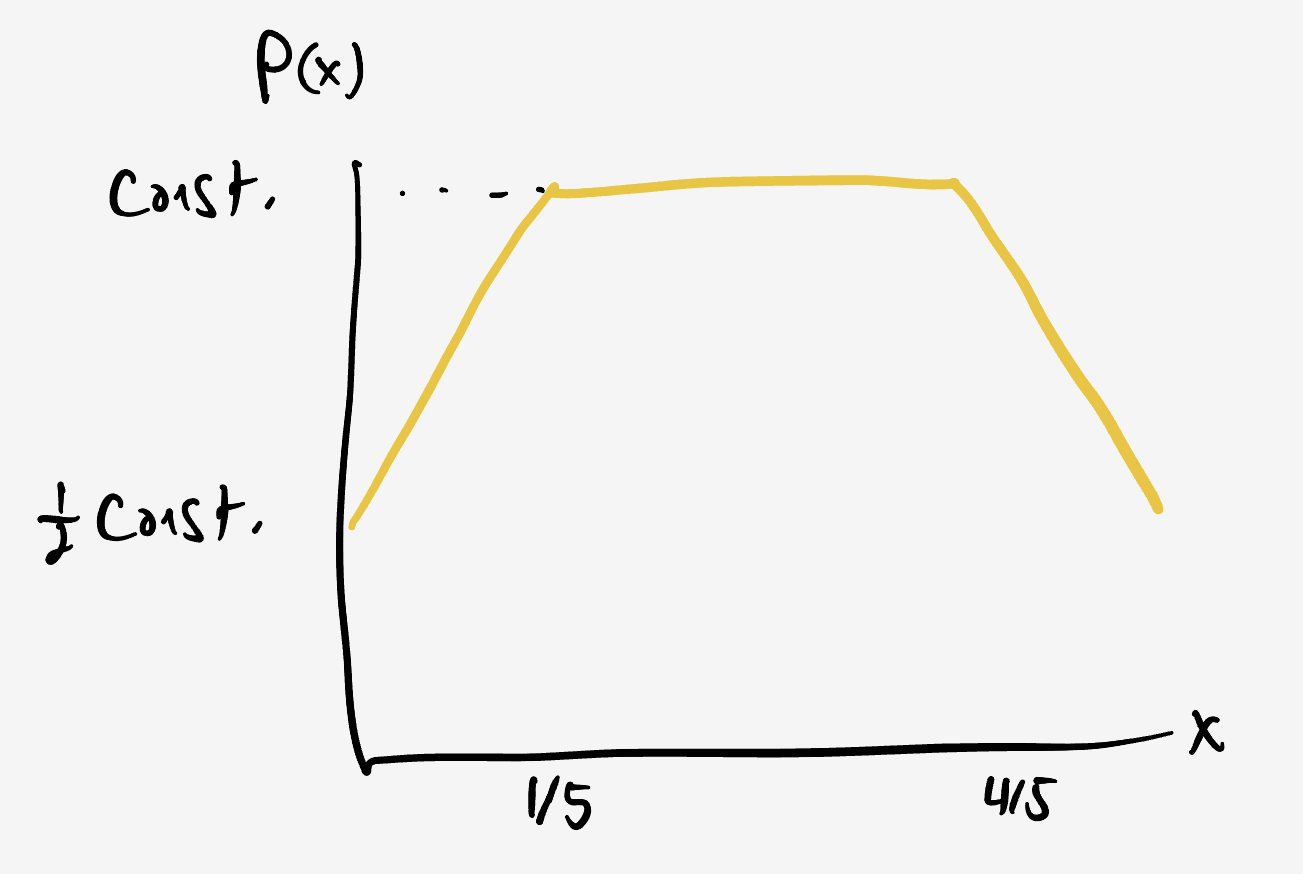
Immediately, we see that the greatest probability is found at any point in the central region, and the lowest probability is found at either edge of the balance beam. Plugging in, we get $\boxed{P(\tfrac15)/P(0) = 2}.$

Grasshopper distribution

The total area under $P(x)$ has to be $1,$ which we can use to find $\text{const.}$ Adding up the central rectangle and the two trapezoids on the wings, we get

which shows that $\text{const.} = 10/9.$

Truth in numbers

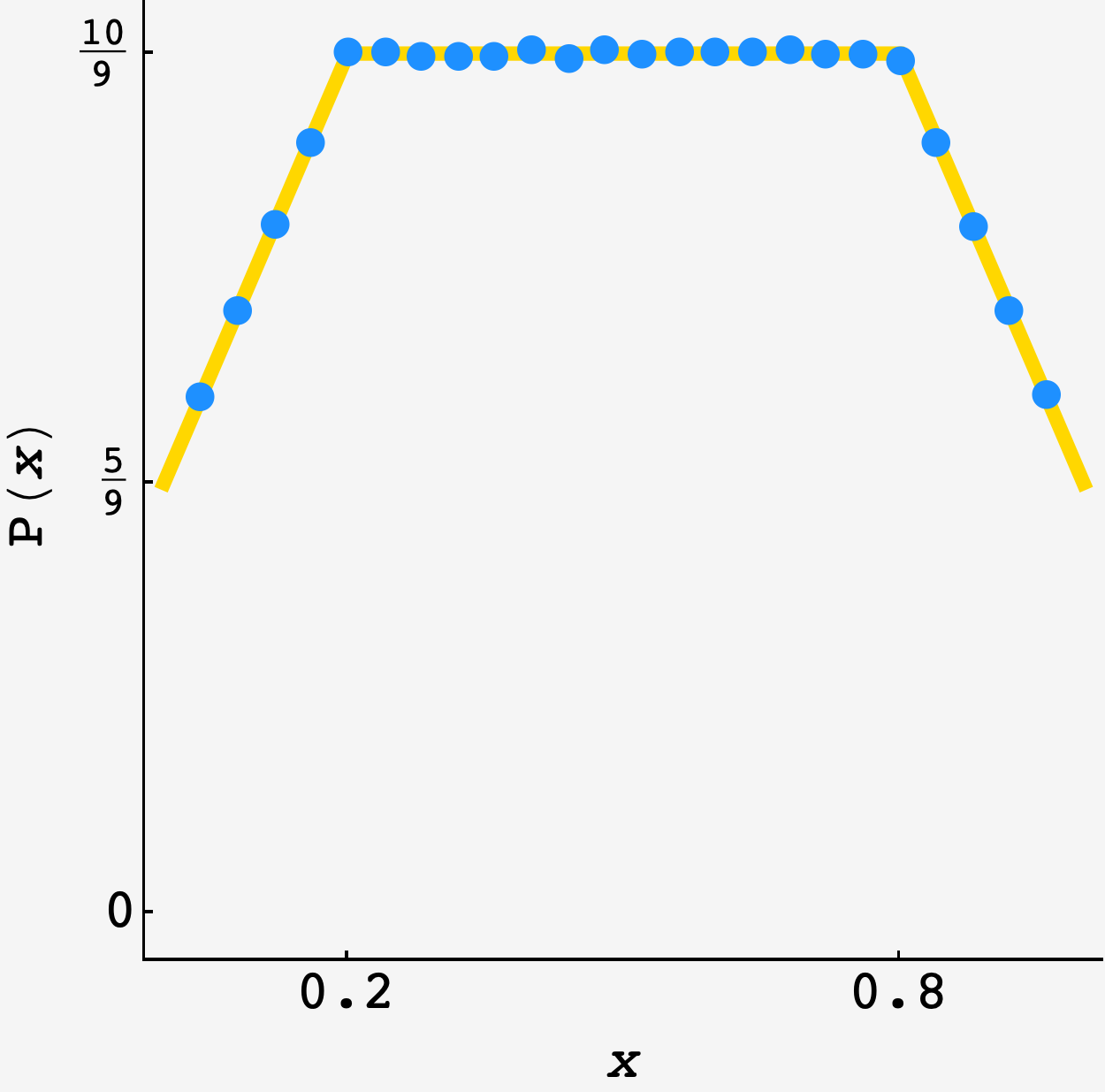
Indeed, an $N=10^6$ simulation produces the data in blue, which is plotted alongside the analytic prediction in gold:

transition[x_] := RandomReal[{Max[0, x - 0.2], Min[1, x + 0.2]}]

round[] := (
  point = 0.5;
  Do[
   point = transition[point]
   , {i, 1, 1000}
   ];
  Return[point]
  )

Pretty good.