Question: It’s year 5 of quarantine and all computing power is reserved for face filters that make you look like a baby or the GEICO lizard. If you want to crunch numbers there’s a new calculator in town — the C. elegans petri dish.
To add two numbers $x$ and $y$ you gather as many nematodes, put them in the dish, and come back the next day to see how many nematodes there are. The nematodes will pair bond (sex doesn’t matter, C. elegans are almost all hermaphroditic) and each pair will procreate (yielding one new worm), or not, with probability $1/2.$
It’s noisy, and it’s random, but that’s the best we can do in these trying times. To raise a number $x$ to the $n^\text{th}$ power, you gather as many nematodes and leave them in the dish for $n$ days, and however many there are upon your return is $x^n.$ Under these rules, what is $(1+1)^n$?
Solution
On the face of it, this addition scheme presents us with a rich cascade of branching paths each of which leads in turn to cascades of their own. Every time we gain two nematodes, we gain another pair, and so unlock new possibilities.
Getting the lay of the land
Let’s take a look at some of the cases.
With two nematodes in the dish, there is $1$ pair which can either reproduce or not, each with equal likelihood. The expected number of nematodes after $1$ step is then
\[\langle w_1\rangle = \frac12 \times 2 + \frac12 \times 3 = 2.5\]In the next step we essentially have the same problem because whether we have $2$ or $3$ nematodes, we can only form $1$ pair. So, the $2$ nematode dish will become either a $2$ or $3$ nematode dish and the $3$ nematode dish will become either a $3$ or $4$ nematode dish. The probabilities are symmetric, so the expectation after $2$ steps is
\[\langle w_2\rangle = \frac14 \times 2 + \frac12 \times 3 + \frac14 \times 4 = 3.\]From here, things start getting more complicated. The branches terminating with $2$ or $3$ nematodes are presented again with the options we’ve already seen. But the branch with $4$ nematodes now has $2$ pairs and so can make jumps of size $0,$ $1,$ or $2,$ — starting the third day with $4,$ $5,$ or $6$ worms. It could be that both pairs fail to procreate yielding $0$ new worms ($ p = 1/2^2$), or that both succeed and yield $2$ new worms (also $p = 1/2^2$), or it could be that one pair succeeds and the other fails, yielding $1$ new worm ($p=2\times 1/2^2 = 1/2$).
Carrying on in this way, we find $\left(1+1\right)^4 = 141/32 \approx 4.41.$
False starts
The branching structures in the above called out to me like an Impossible burger in the desert. Indeed, there are some interesting patterns (like how the branching options from $w$ or $\left(w+1\right)$ (where $w$ is even) can be generated by $(1+z)^{\lfloor w/2\rfloor}/2^{\lfloor w/2 \rfloor}$) that proved awfully tempting for a generating function enthusiast like me. Sadly, there wasn’t enough Saturday to probe the depths of their beauty and, so, they remain waiting patiently for future inspection.
Another futile effort was to cast the transitions between petri dishes in the language of bras and kets, in search of a propagator. Though this led nowhere analytically, it gave a path for computing exact our results, which we’ll use to confirm the approximation below.
Physics
Ultimately, what led to real progress was good old fashioned physics chutzpah.
When there are $w$ worms in the dish, there are roughly $w/2$ pairs.
We expect half of these pairs to procreate, yielding $1/2\times w/2 = w/4$ new worms. So, on average, one day in the dish produces the transition
\[\begin{align} w &\rightarrow w + w/4 \\ &= w\times\left(1 + \frac14\right) \end{align}\]and after $t$ days
\[w_t \approx w_0\times \left(1+\frac14\right)^{t-1}.\]So, we expect the mean number of worms to go like
\[\boxed{\langle w_t\rangle \approx 2\times \left(\dfrac54\right)^{t-1}}.\]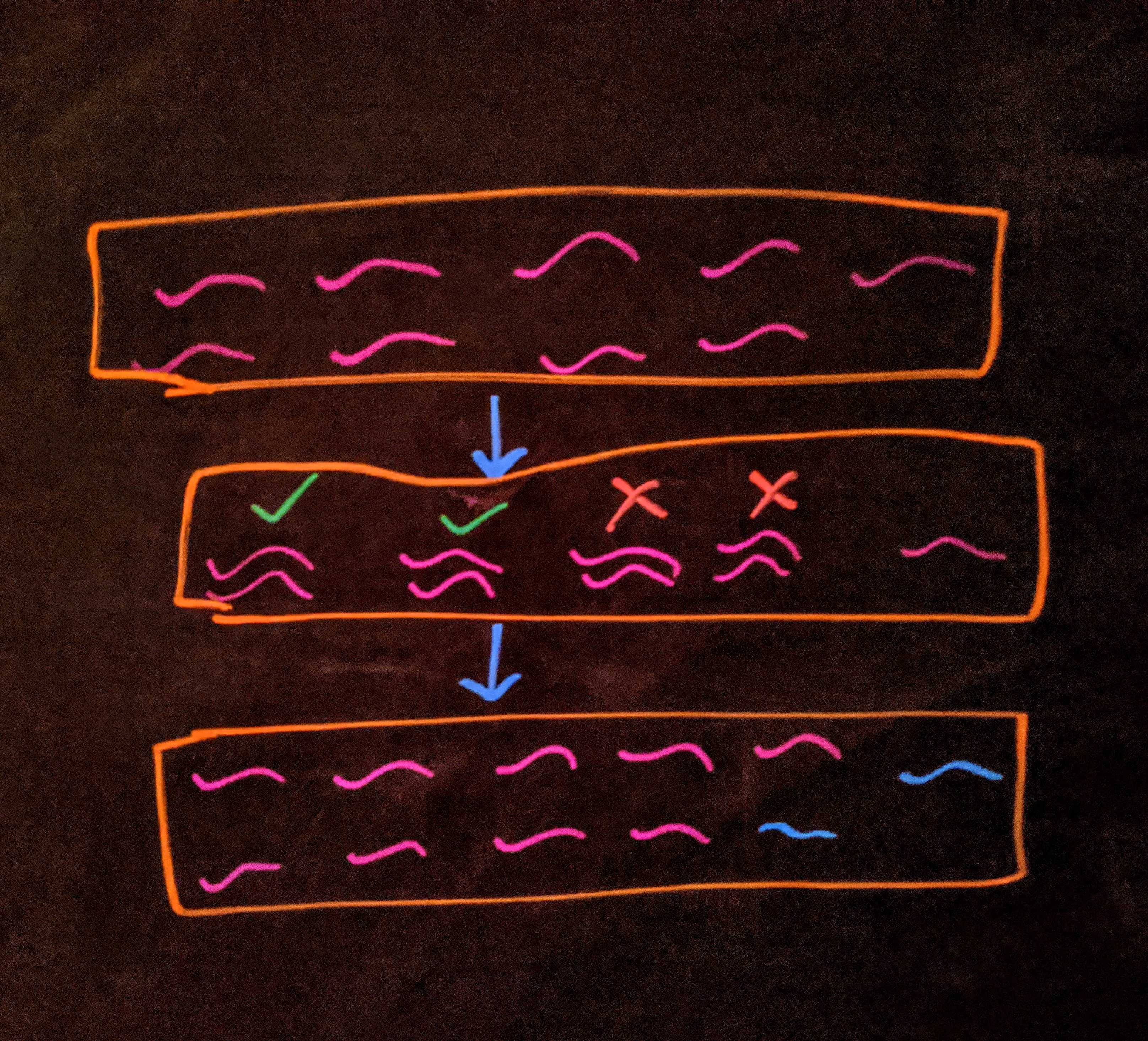
Diagram of the approximation
At early times this estimate will underwhelm, since the gap between mean (e.g. $2.5$) and realizable states (e.g. $2$ and $3$) is significant. But as time goes on, the mean behavior dominates and the approximation will get better and better. As we’ll see below, by day $15$ in the dish, the mean prediction is good to within $1\%.$
Exact computation
If we have the probability of going from one number of nematodes to another in the span of a day, we can put them in a transition matrix $\mathbf{T}.$ Likewise, we can store the information about the probability distribution for the number of nematodes in various realizations of the system in a vector like $\vert \psi_t\rangle = \left(p_1, p_2, \ldots, p_n\right).$ In this representation, we can get the proabability distribution on day $n$ by operating on $\vert\psi_0\rangle$ with the matrix $\mathbf{T}$, $n$ times: \(\vert\psi_t\rangle = \mathbf{T}^n \cdot \vert\psi_0\rangle\)
We can write each element of the transition matrix like $p_{i\leftarrow j} \vert i\rangle\langle j\vert$ where $p_{i\leftarrow j}$ is the probability of moving from a $j$ nematode dish to a $i$ nematode dish, and $\vert i\rangle\langle j\vert$ indicates that it’s the $\left(j,i\right)$ entry in the matrix.
Writing out all the terms relevant for the first three days (where we’ll generate at most $6$ nematodes), we have
\[\mathbf{T} = \frac12 \vert 3\rangle\langle 2\vert + \frac12 \vert 2\rangle\langle 2\vert + \frac12 \vert 4\rangle\langle 3\vert + \frac12 \vert 3\rangle\langle 3\vert + \frac{1}{2 ^2}\vert 4\rangle\langle 4\vert + \frac{1}{2}\vert 5\rangle\langle 4\vert + \frac{1}{2 ^2}\vert 6\rangle\langle 4\vert + \ldots\]In general, the probability of the $i\leftarrow j$ transition is equal to the number of ways of having $i-j$ procreations out of $\lfloor j/2\rfloor$ pairs divided by $2^{\lfloor j/2\rfloor}$:
\[T_{ji} = \dfrac{1}{2^{\lfloor j/2\rfloor}}\dbinom{\lfloor j/2\rfloor}{i-j}\]Once we have $\vert\psi_t\rangle,$ we can simply take its dot product with the vector $\left(1,2,\ldots,\max w\right)$ to get the expectation value
\[\langle w \rangle = \left(\mathbf{T}^t\vert\psi_t\rangle\right)\cdot\left(1,2,\ldots,\max w\right)\]To find the greatest possible number of worms on day $t$, each of the $\lfloor w/2\rfloor$ pairs would have to successfully reproduce each day which would increase the number of worms by $50\%,$ so, $\max w_t = \lfloor \frac32 \max w_{t-1}\rfloor.$ We can use this to set the size of our matrix and composition vectors.
Coding this up, we get
highest[1] = 2;
highest[n_] := Floor[3/2 highest[n - 1]];
T[NN_] := (
Table[
Table[
If[j <= i, Binomial[Floor[j/2], i - j]/2^Floor[j/2],
0],
{j, 1, NN}],
{i, 1, NN}
])
support[day_] :=
MatrixPower[SparseArray[T[highest[day]]], day - 1].
Table[If[i == 2, 1, 0], {i, 1, highest[day]}]
data = {};
For[day = 1, day <= 23, day++,
AppendTo[data, {day, support[day].Table[i, {i, 1, highest[day]}]}];
];
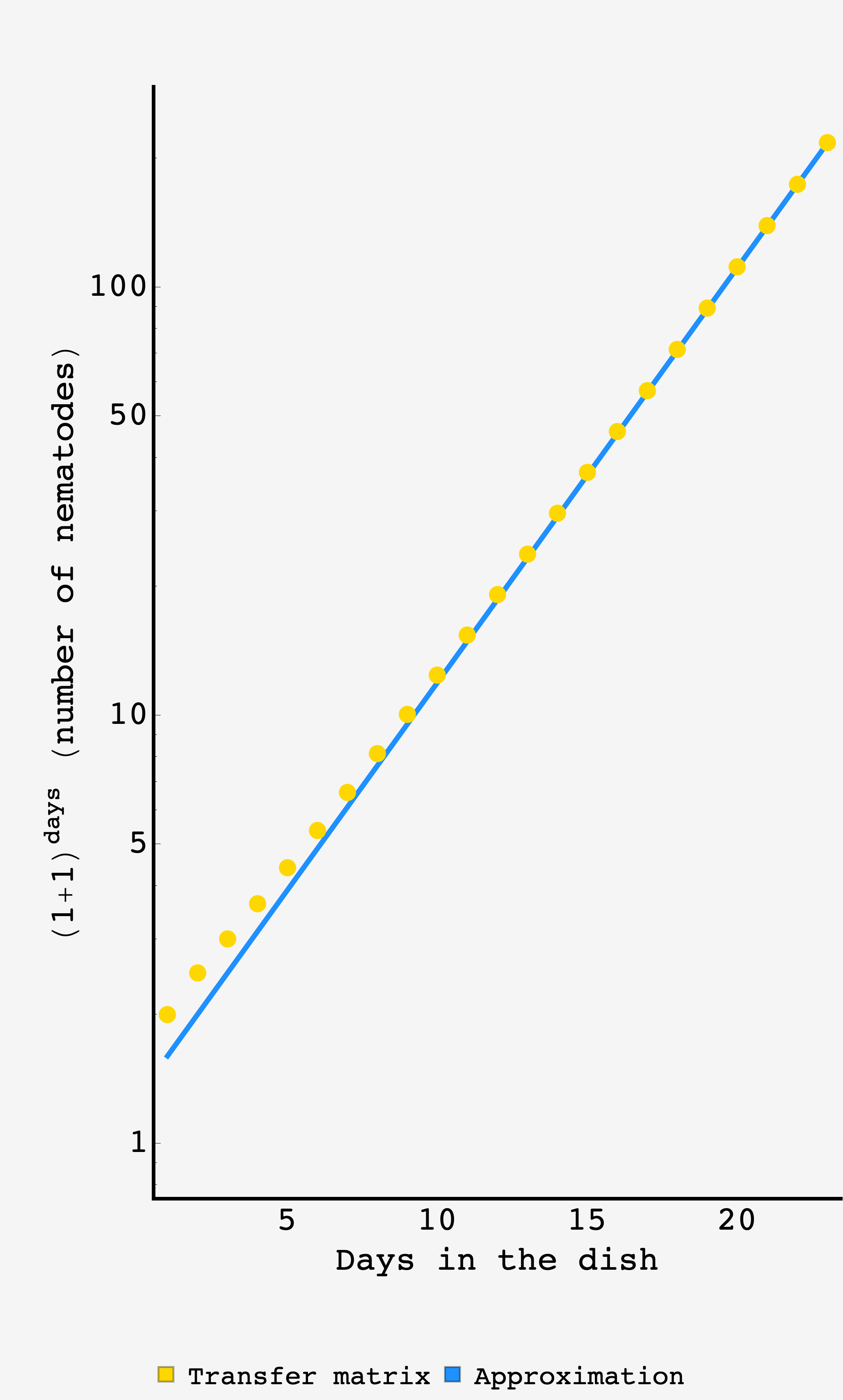
Comparison of the exact result with transfer matrices to the back of the envelope approximation.