Question: Quality control at your ruler factory has taken a turn for the worst and your latest shipment of rulers are all broken into 4 pieces! What is the average length of the shard that contains the $\text{6 inch}$ mark?
Solution
At first I solved the $4$-piece case with a cobbled-together multivariable integral, to get $\langle\ell\rangle = 15/32$, I expected the $N$-piece case to involve sums of compound integrals and was going to leave it alone. However, in light of compelling empirical results from Goh Pi Han, we were inspired to look for a simple perspective.
The approach is to find the probability distribution for the length of the shard that includes the $\text{6 inch}$ mark ($x=1/2$ for the purpose of this solution). The main insight is that for a length $\ell$ interval to cover the point $1/2,$ all we need is that two points are a distance $\ell$ apart and that no other points interrupt that interval (or else it would become a covering interval of length $\ell^\prime < \ell$).
Does it cover?
The first non-trivial issue here is the probability that a random interval of length $\ell$ will cover the point $1/2.$
First of all, if $\ell \geq 1/2,$ then this probability is $1$ — there’s no way to place an interval of length $\ell > 1/2$ without encompassing the middle of the ruler. So, whatever expression we find, we expect it to equal $1$ when $\ell = 1/2.$
For a ruler of length $\ell,$ the total length of the region where we can place the shard’s leftmost point is $\left(1-\ell\right)$ (we can’t place it any further, or its rightmost point would include points not on the original ruler). And if the shard’s leftmost point starts more than a distance $\ell$ away, it won’t reach $1/2.$
So, the probability that a random shard of length $\ell$ covers the halfway point is $P_\text{cover} = \ell/(1-\ell),$ which equals $1$ when $\ell = 1/2,$ as we had hoped. To summarize,
\[P_\text{cover}(\ell)=\begin{cases} \dfrac{\ell}{1-\ell} & \text{when } \ell \lt 1/2 \\ 1 & \text{when } \ell \geq 1/2. \end{cases}\]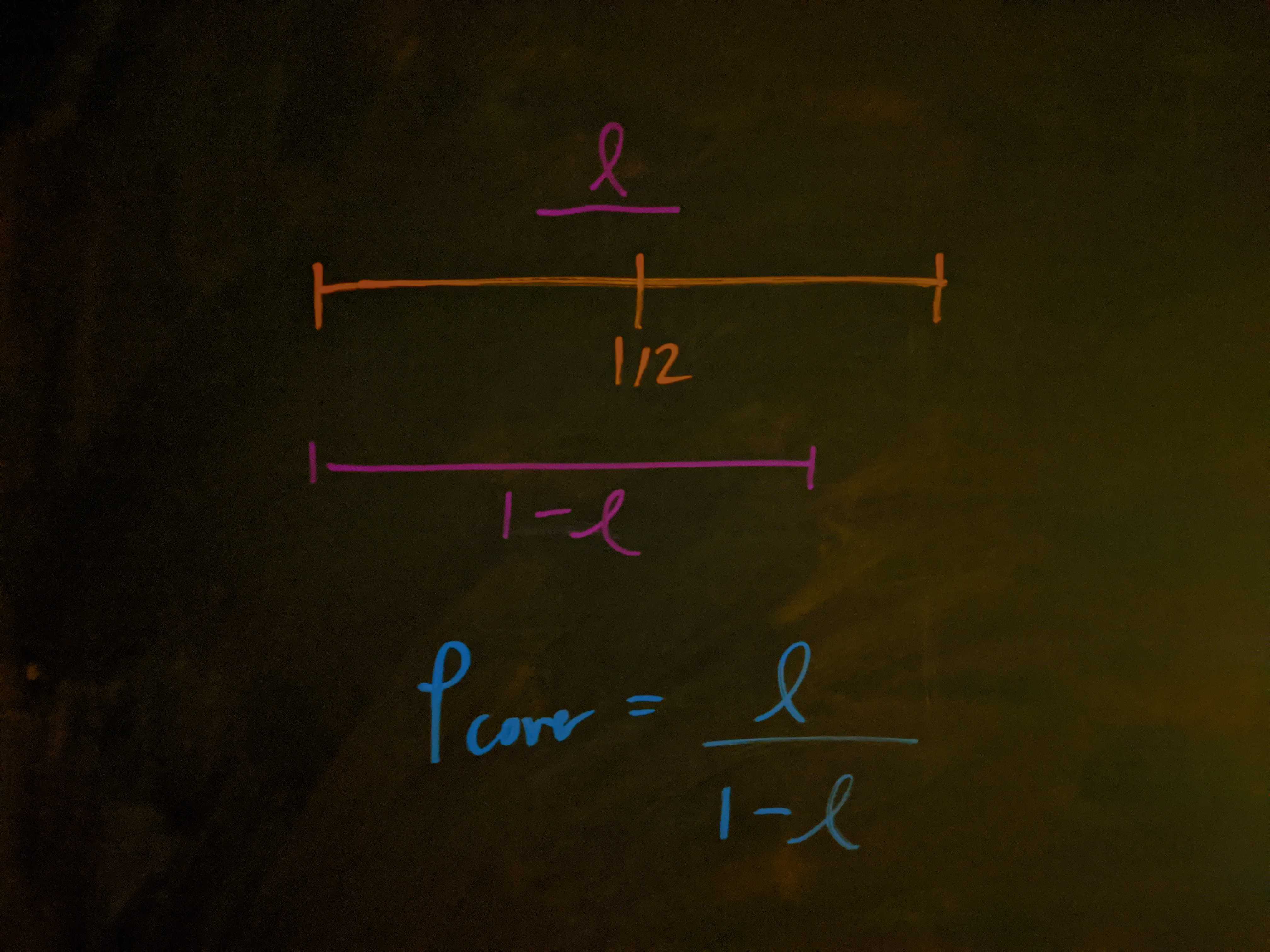
Cases
There are two umbrella cases:
- where the shard is formed from two points where the ruler has broken. When $\ell < 1/2$, this is the only way for the shard to form.
- when $\ell \geq 1/2$ it becomes possible for the shard to stretch all the way from an original endpoint of the ruler (say the $0\text{ inch}$ mark) past $1/2.$
Two breakpoints
The first case involves several things: a. the random interval has to contain $1/2,$ b. no points can be within $\ell$ of the left end of the shard, c. the right end of the shard has to be a distance $\ell$ from the left end, d. the number of ways we can pick $2$ endpoints out of the $n$ breakpoints ${x_1,x_2,\ldots,x_n}.$

Parts a and b contribute $P_\text{cover}(\ell)\times \left(1-\ell\right)^{n-1}.$ Part d contributes $2\times\binom{N}{2}$ (the $2$ because $x_i$ on the left with $x_j$ on the right is distinct from the reverse). Part c is a bit tricky. The first and last point have to be chosen a distance $\ell$ apart. However, each point is a random draw of uniform probability. As we’ve already ensured that the other $\left(n-1\right)$ points are a distance of at least $\ell$ from the first, this factor is just $1.$
In total, the distribution of lengths $\ell$ for a shard with two breakpoints for ends is
\[P_2(\ell) = 2\binom{n}{2}P_\text{cover}(\ell)\left(1-\ell\right)^{n-1}.\]One breakpoint
For the case where only one end of the shard is a breakpoint, the calculation is straightforward. The first point is picked with uniform probability, all $\left(n-1\right)$ remaining points have to be picked outside of the interval $\left[0,x\right),$ and there are $\binom{N}{1}$ ways to select the first point. Since there’s a symmetric set of cases when the unbroken endpoint is at the $\text{12 inch}$ mark, we multiply by $2$. Since such a shard must have $\ell\geq 1/2$, there is $100\%$ chance for this shard to cover $1/2.$
Putting it all together, the one breakpoint shard’s distribution is
\[P_1(\ell) = \begin{cases} 0 & \text{when } \ell \lt 1/2 \\ 2\binom{n}{1}\left(1-\ell\right)^{n-1} & \text{when } \ell \geq 1/2. \end{cases}\]
Complete pdf
With these two cases in hand, the overall pdf is just $P_\text{total}(\ell) = P_1(\ell) + P_2(\ell)$ which has a jump discontinuity at $\ell=1/2$. When $\ell<1/2$ there’s just the two-breakpoint shard, and
\[\begin{align} P_\text{total}(\ell) &= 2\binom{n}{2}P_\text{cover}(\ell)\left(1-\ell\right)^{n-1} \\ &= 2\binom{n}{2}\frac{\ell}{1-\ell}\left(1-\ell\right)^{n-1} \\ &= 2\binom{n}{2}\ell\left(1-\ell\right)^{n-2} \end{align}\]When $\ell \geq 1/2,$ both kinds of shard are possible and (with $P_\text{cover}(\ell) = 1$ when $\ell > 1/2$), we have
\[\begin{align} P_\text{total}(\ell) &= 2\binom{n}{2}\left(1-\ell\right)^{n-1} + 2\binom{N}{1}\left(1-\ell\right)^{n-1} \\ &= 2\left(1-\ell\right)^{n-1}\left[\binom{n}{1} + \binom{n}{2}\right] \\ &= 2\left(1-\ell\right)^{n-1}\binom{n+1}{2} \end{align}\]So
\[P_\text{total}(\ell) = \begin{cases} 2\binom{n}{2}\ell\left(1-\ell\right)^{n-2} & \text{when } \ell \lt 1/2 \\ 2\binom{n+1}{2}\left(1-\ell\right)^{n-1} & \text{when } \ell \geq 1/2 \end{cases}\]Plotting this against an empirical pdf with $N=10\, 000$ points, it looks pretty good:

Expected shard length
With the pdf in hand, we can find $\langle\ell\rangle$ by integration:
\[\begin{align} \langle\ell\rangle &= \int\limits_0^\ell d\ell\, \ell \times P_\text{total}(\ell) \\ &= 2\binom{n}{2}\int\limits_0^{1/2} d\ell\, \ell^2 \left(1-\ell\right)^{n-2} + 2\binom{n+1}{2}\int\limits_{1/2}^1 d\ell\, \ell\left(1-\ell\right)^{n-1} \end{align}\]which comes out to the absolutely miraculous
\[\boxed{\langle\ell\rangle = \frac{2-2^{-n}}{n+1}}.\]Plugging in values $n,$ we find the expected lengths for the first few number of breakpoints, reproducing $15/32$ for $n=3$ breaks, as we expect:
\[\begin{array}{|c|c|}\hline n & \langle\ell\rangle \\ \hline 0 & 1 \\ 1 & \frac{3}{4} \\ 2 & \frac{7}{12} \\ 3 & \frac{15}{32} \\ 4 & \frac{31}{80} \\ 5 & \frac{21}{64} \\ 6 & \frac{127}{448} \\ 7 & \frac{255}{1024} \\ 8 & \frac{511}{2304} \\ 9 & \frac{1023}{5120} \\ 10 & \frac{2047}{11264} \\ \hline \end{array}\]