Question: Tortoise and Hare are having a stroll down a 10 mile road — Tortoise can run at a healthy clip of $60$ mph while Hare can run at an even healthier clip of $75$ mph. But that’s not all… the road is magic and every minute, on the minute, the road is stretched uniformly by $10$ miles. If Tortoise and Hare want to finish their stroll at the same time, how long should Hare hang back after Tortoise gets started?
Solution
On the standard issue road that doesn’t magically extend by $10$ miles every minute, the problem is a bit simpler. Because Hare can cover $25\%$ more ground than Tortoise in the same amount of time, they should wait until the distance that Tortoise has left to go is $4/5$ of the distance that Hare has left to go, i.e., $4/5\times 10\,\text{miles} = 8\,\text{miles}$.
As it happens, this is the key to the rubber band road as well.
When Tortoise starts walking down the rubber band road, they make it $1\,\text{mile}$, or $10\%$ of the way, before the road stretches. While this stretch adds road to the path before them, it does nothing to affect the fractional progress they’ve made along the road.
In other words, whenever Hare starts down the road, they are going to be dealing with the same problem as Tortoise, just longer. All of the proportional stretching from that point on will be identical for Tortoise and Hare.
So, as on the non-magical road, Hare should start when Tortoise is $20\%$ of the way to the end of the road.
Tortoise
Every minute, the tortoise travels a distance $\Delta_T = v_T\times \text{1 min}$ and then the road stretches by the factor $(t+1)/t$. This makes the tortoise position as a function of time (using integer numbers of minutes):
\[d_\text{tortoise}(t) = \left[d_\text{tortoise}(t-1) + \Delta_T\right]\frac{t+1}{t}\]Recursing one step,
\[\begin{align} d_\text{tortoise}(t) &= \left(\left[d_\text{tortoise}(t-2) + \Delta_T\right]\frac{t}{t-1} + \Delta_T\right)\frac{t+1}{t} \\ &= d_\text{tortoise}(t-2)\frac{t+1}{t-1} + \Delta_T\frac{t+1}{t-1} + \Delta_T\frac{t+1}{t} \end{align}\]Continuing on in this way we get to
\[d_\text{tortoise}(t) = d_\text{tortoise}(0)\left(t+1\right) + \Delta_T\left(t+1\right)\left(1 + \frac12 + \frac13 + \cdots + \frac1t\right)\]but since $d_\text{tortoise}(0) = 0$ and the sum is the $t^\text{th}$ Harmonic number, this is just
\[d_\text{tortoise}(t) = \Delta_T\left(1+t\right)H(t)\]Unless they hit the finish line in a multiple of minutes, they’ll have a small fraction of the journey they happens after the last road stretching. With this in mind, Tortoise’s distance becomes:
\[d_\text{tortoise}(t) = \Delta_T\left(1+\lfloor t\rfloor\right)H(\lfloor t\rfloor) + \Delta_T\left(t - \lfloor t\rfloor\right)\]The finish line
The position of the finish line is just $\Delta_L\left(1+\lfloor t\rfloor\right)$ which means that Hare should begin when $d_\text{tortoise}(t) = 20\% \times \left(1 + \lfloor t\rfloor\right)\Delta_L$ or
\[\begin{align} \Delta_T\left(1+\lfloor t\rfloor\right)H(\lfloor t\rfloor) + \Delta_T\left(t - \lfloor t\rfloor\right) &= 20\%\times \Delta_L\left(1+\lfloor t\rfloor\right)\\ &= 2\left(1+\lfloor t\rfloor\right) \end{align}\]The fractional part is less than $1$ by definition, so we can drop it and see when the harmonic pieces alone would eclipse the right hand side:
\[\left(1 + \lfloor t\rfloor\right)H(\lfloor t\rfloor) > 2\left(1 + \lfloor t\rfloor\right).\]As the $\left(1+\lfloor t\rfloor\right)$ factor drops out, we just need to find the first time when $1 + \frac12 + \frac13 + \ldots + \frac{1}{t} > 2,$ which is when $t=4$. This means that Tortoise is $20\%$ along the road sometime between the third and fourth minutes.
So, with $\Delta_T = 1,$ the fractional part of the time is
\[\begin{align} \left(t - \lfloor t\rfloor\right) &= 2\left(1 + 3\right) - \left(1+ 3\right)H\left( 3\right)\,\text{min}\\ &=8 - 4\times H(3)\,\text{min} \\ &= \frac23\,\text{min}, \end{align}\]so Hare should start $3$ minutes and $40$ seconds after Tortoise.
Checking Our Work
To figure out when the race finishes, we apply the same logic from above, but now looking for when Tortoise is at $100\%$ the length of the road. This means we want the first $\lfloor t\rfloor$ for which $H(\lfloor t\rfloor) > 10.$ We can solve this numerically to find $\lfloor t\rfloor = 12367\,\text{min}.$ So, the final road stretch will occur at $t = 12366\,\text{min}$ and we can solve the linear equation for the crossing at
\[t_\text{finish} = 12366 + 123670 - H(12366) (1 + 12366) \approx 12366.468116653079\,\text{min}.\]We can plug the $3$ minutes $40$ second delay time into the expressions for Tortoise and Hare’s distance, and plot their position over time. Indeed they overlap with the finish line at exactly the same time.
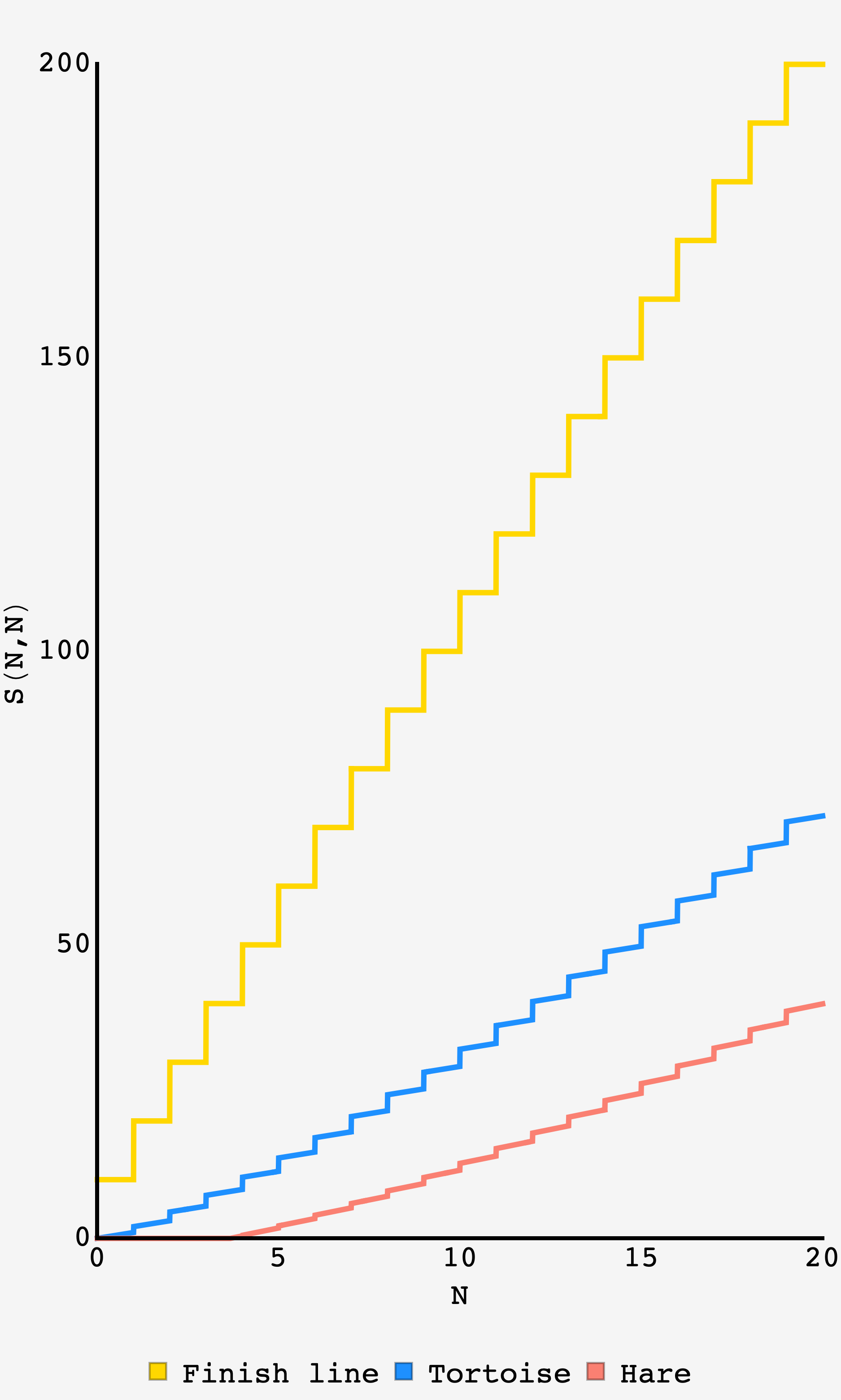
Plot of the finish line, tortoise, and hare over the first $20$ mins of the stroll.
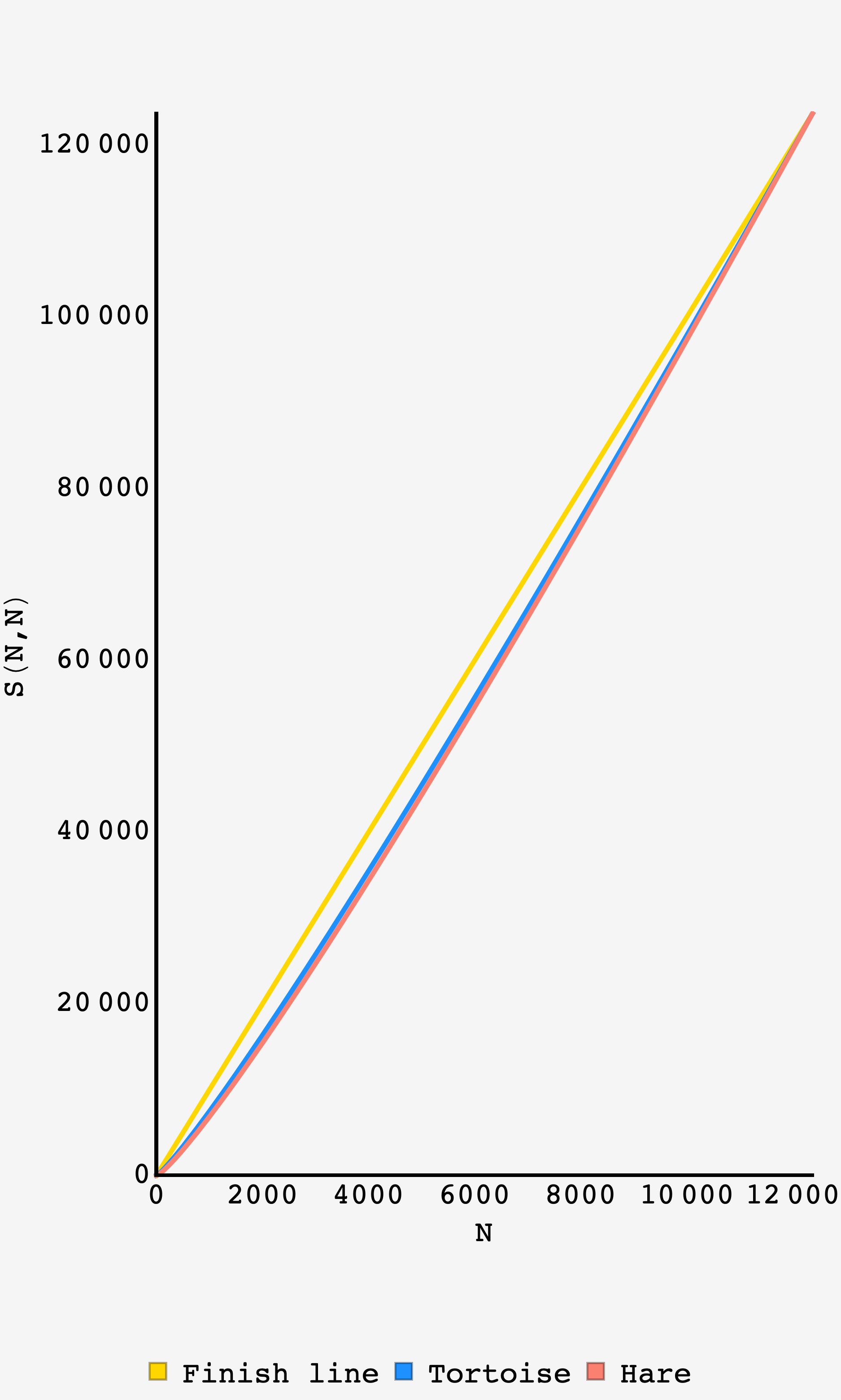
Plot of the finish line, tortoise, and hare over the entire stroll.
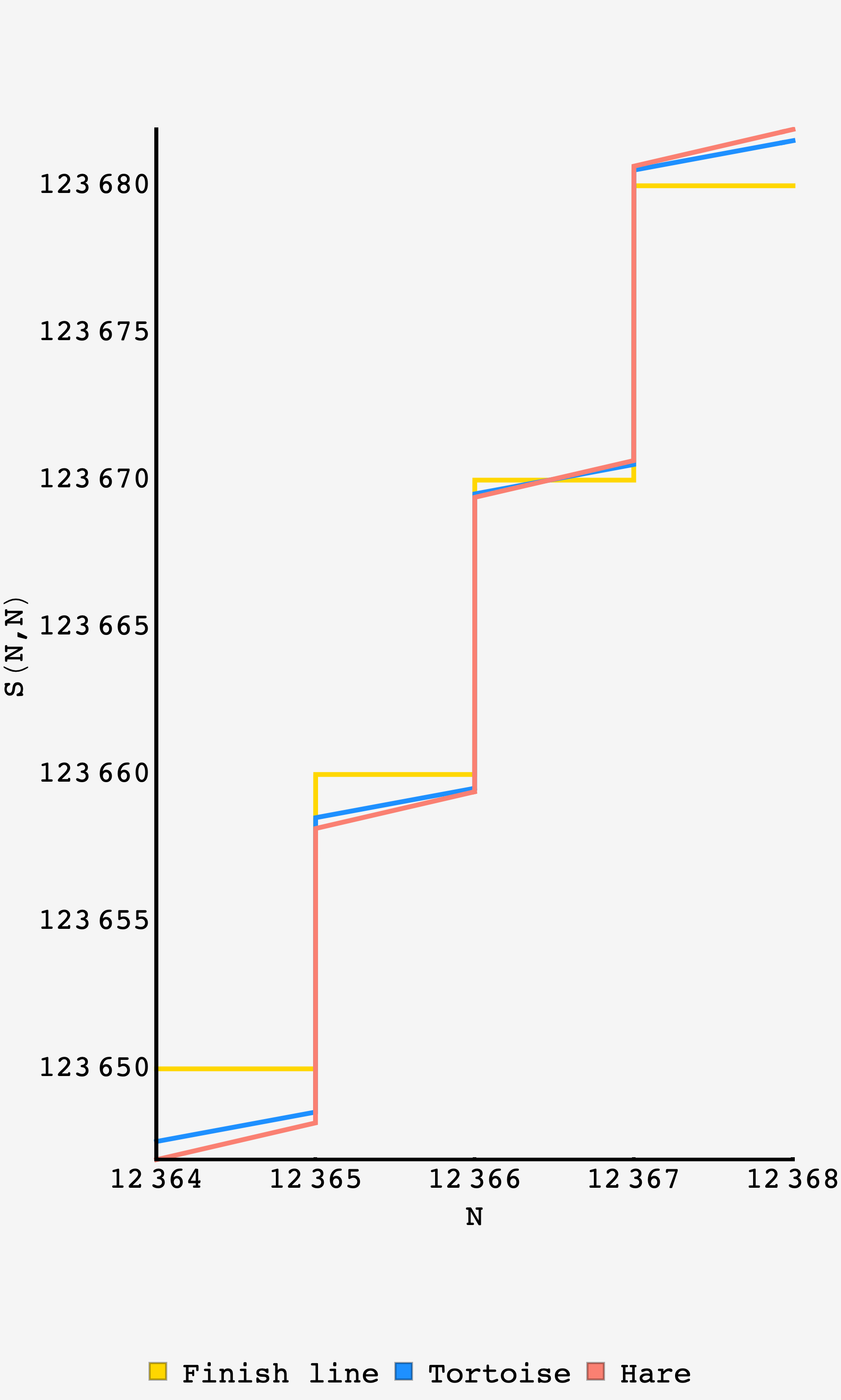
Plot of the finish line, tortoise, and hare intersecting at the end of the stroll, $t_\text{finish} \approx 12366.4.$
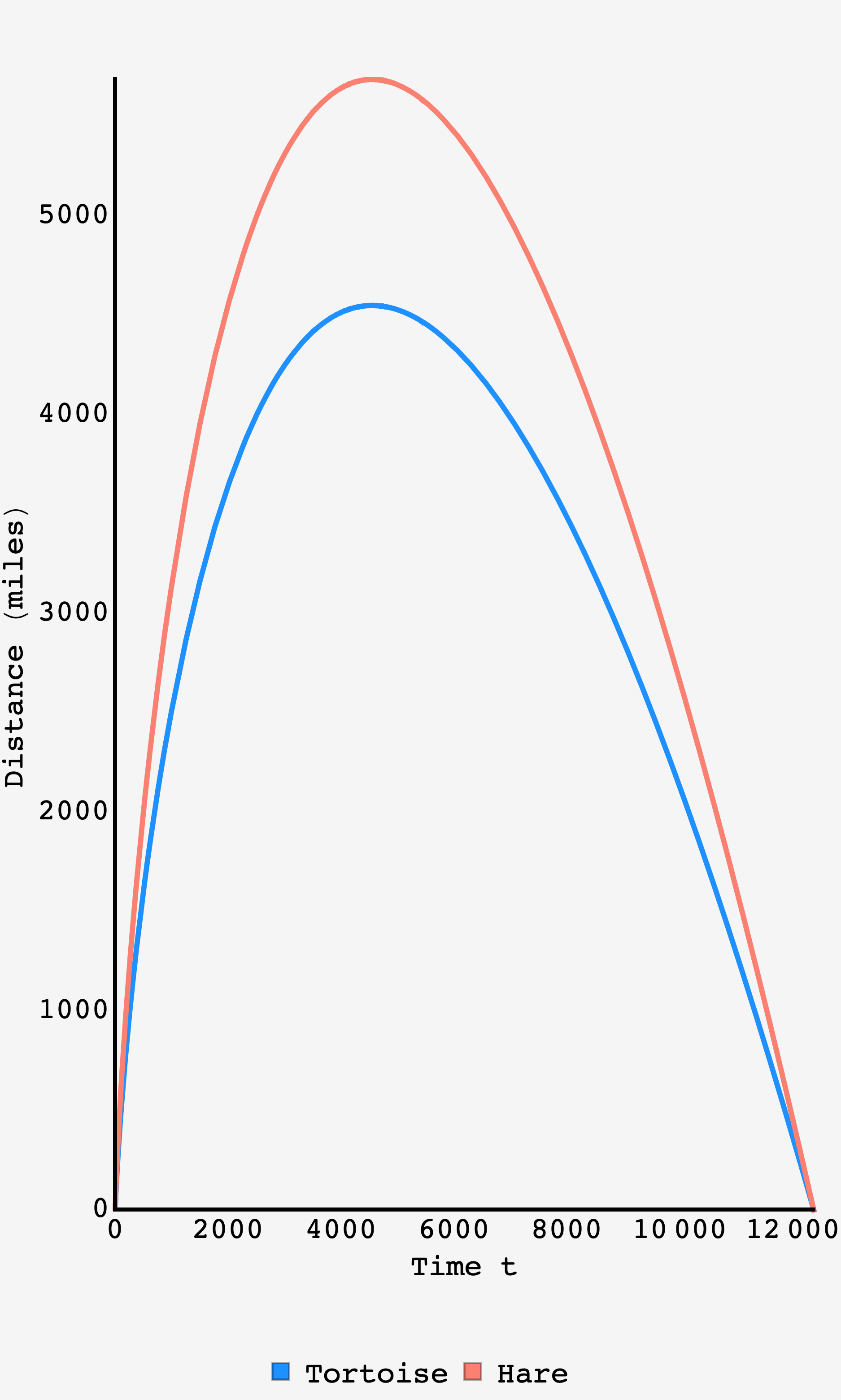
Plot of the tortoise and hare’s distance relative to the finish line throughout the stroll.
For reference, Hare’s position over time is equal to
\[\begin{align} d_\text{hare}(t,t_\text{start}) &= \left(\lceil t_\text{start}\rceil - t_\text{start}\right)\Delta_H \frac{1 + \lfloor t\rfloor}{1 + \lfloor t_\text{start}\rfloor} \\ &+ \Delta_H\left(1+\lfloor t\rfloor\right)\left[H(\lfloor t\rfloor) - H\left(\lfloor t_\text{start}\rfloor + 1\right)\right] \\ &+ \Delta_H \left(t - \lfloor t\rfloor\right), \end{align}\]where $\Delta_H = 5/4.$