Question: A circle is randomly generated by sampling two points uniformly and independently from the interior of a square and using these points to determine its diameter. What is the probability that the circle has a part of it that is off the square?
Solution
There are two ways to go after this problem. We can measure the volume of coordinate space devoted to interior circles, or we can go after the probability directly.
Measurement
In the first approach, what we want to measure is
\[\int dx_1 \int dy_1 \int dx_2 \int dy_2\ \mathbb{I}(\text{diameter forms interior circle}\rvert x_1,x_2,y_1,y_2),\]the volume of $(x_1,y_1,x_2,y_2)$-space that contributes to interior circles (diameters whose circle is contained in the unit square).
Instead of thinking in terms of the two points in $4$-space, we can think about the problem in terms of the center and radius of the resulting circle:
\[\begin{align} x_c &= \frac12\left(x_1 + x_2\right) \\ y_c &= \frac12\left(y_1 + y_2\right) \\ x_r &= \frac12\left(x_1 - x_2\right) \\ y_r &= \frac12\left(y_1 - y_2\right). \end{align}\]How many positions can the center take? For a circle of radius $r,$ the center can occupy any position inside the $(1-2r)$ by $(1-2r)$ sub-square inside the unit square.
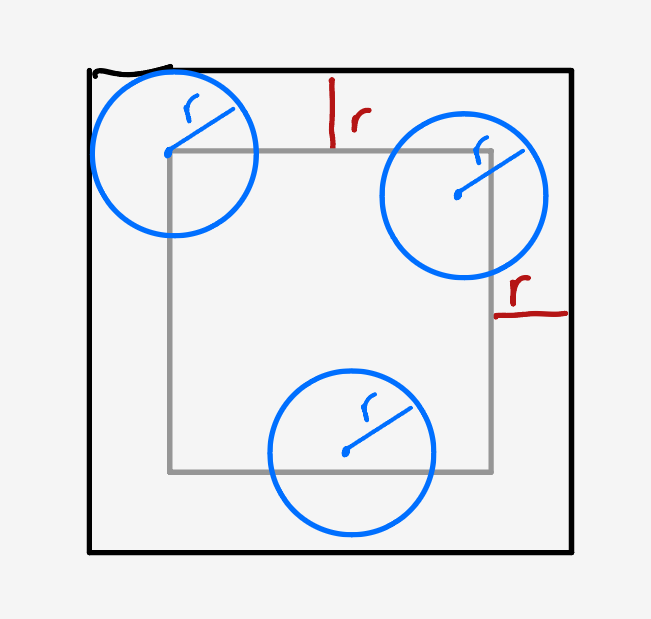
Each point on the circle represents a pair (the point itself, and the point across from it on the same circle). The number of such pairs is proportional to the annulus of area $(2\pi r)\text{d}r$ about the center.
Since we’re just counting coordinate space, we can sum over all such centers and radii:
\[P(\text{interior circle}) \propto \int dr\, 2\pi r(1-2r)^2.\]But we need to be careful about the unit area in the new coordinates. In moving to the (center, separation) coordinate system, we shrink each unit vector by a factor of $1/\sqrt{2}.$
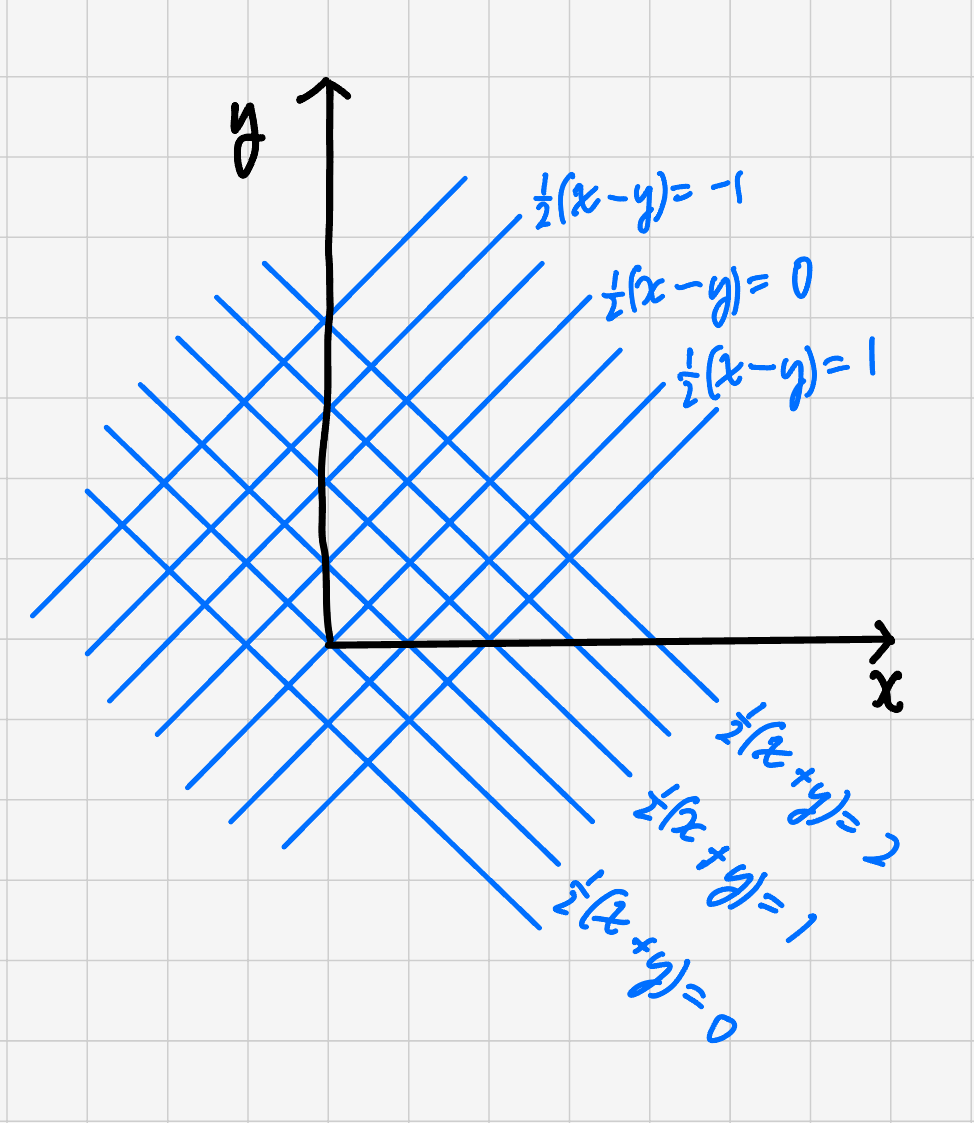
We can see this by calculating the magnitude of e.g. $d\vec{x}_c$ or by calculating the area element $dA = dx_1\,dx_2$ in terms of $dx_c$ and $dx_r.$
Taking a derivative, we get $d\vec{x}_c = \frac12\left(d\vec{x}_1 + d\vec{x}_2\right)$ which has magnitude $\frac12\sqrt{dx_1^2 + dx_2^2} = \frac{1}{\sqrt{2}}dx_1.$
Taking cross products, we get $dA = \lvert d\vec{x}_c\times d\vec{x}_r\rvert = \lvert\frac14\left(d\vec{x}_1\times d\vec{x}_2 + d\vec{x}_2\times d\vec{x}_1\right)\rvert = \frac12 dx_1dx_2,$ which gives us
\[dx_c\,dx_r = \frac12dx_1\,dx_2.\]So, $dx_1\,dx_2\,dy_1\,dy_2 = 4dx_c\,dx_r\,dy_c\,dy_r.$ With this, we can finish the expression for the volume of coordinate space contributed by circles of diameter $2r:$
\[dr\, 8\pi r(1-2r)^2.\]Integrating over all valid radii, we get
\[\begin{align} P(\text{interior circle}) &= 8\pi\int\limits_0^\frac{1}{2}dr\, r(1-2r)^2 \\ &= 8\pi \int\limits_0^{\frac12}dr\, \frac12\left[(1-2r)^2 - (1-2r)(1-2r)^2\right] \\ &= 2\pi \int\limits_0^1 du\, \left[(1-u)^2 - (1-u)^3\right] \\ &= \frac{\pi}{6}, \end{align}\]and the probability that a random such circle overlaps the outside is
\[P(\text{overlap}) = 1 - \frac{\pi}{6}.\]This approach is nice apart from the unit area changing under our feet.
Probability
Let’s write the probability that a random pair of points makes an interior circle as
\[P(\text{interior}).\]This is hard, but we can condition on the circle’s radius.
\[P(\text{interior}) = \int dr\, P(\text{interior}\rvert r)P(r).\]This gives us two new distributions to find, the probability that a random circle of radius $r$ is interior, and the probability that a random circle has radius $r.$
Finding $P(r)$
Let’s do the second piece first.
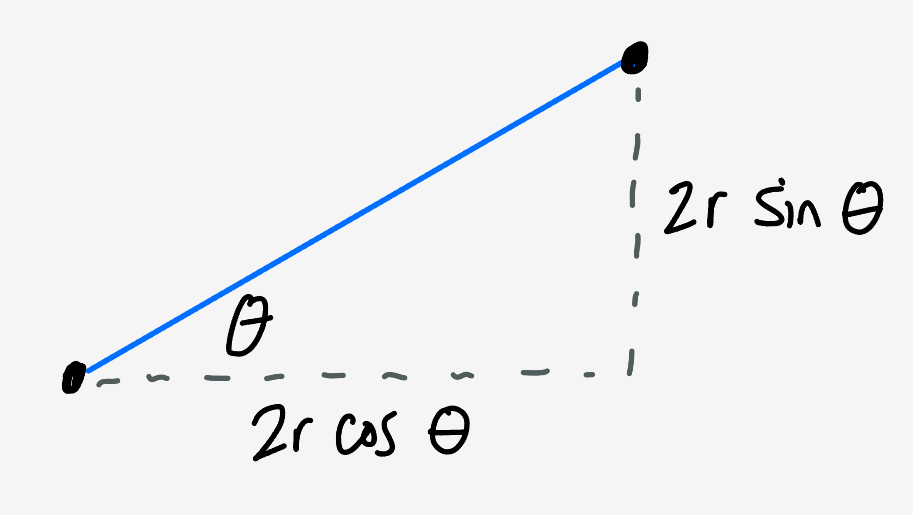
The probability to get radius $r$ is the probability that the $x$ and $y$ components of the diameter form a vector of magnitude $2r.$
\[P(r) = \int d\theta\, P(\text{$x_1-x_2 = 2r \cos\theta$})P(\text{$y_1-y_2 = 2r \sin\theta$}).\]Since we pick the points randomly, we can treat the $x$ and $y$ coordinates independently. The probability that two random unit variables are separated by a distance $d$ is just $2(1-d).$
To see this, we can place two points a distance $d$ apart on a line with the left hand point starting out at the origin. There is $(1-d)$ worth of open space to slide them before the right hand point hits $1.$ Since we can swap the order of the points and get another valid arrangement, we get a factor of $2.$
Now, the angle of the diameter is random, so we have to average over it. Putting this all together, $P(r)$ is
\[\begin{align} P(r) &= 4\int\limits_0^{\frac12\pi} d\theta\, 4(1-2r\cos\theta)(1-2r\sin\theta) \\ &= 8r(\pi -4(2-r)r). \end{align}\]Finding $P(\text{interior}\rvert r)$
This piece is straightforward in concept, but tricky to calculate.
If we randomly place the center of the circle at coordinates $(x_c,y_c),$ what is the probability that it forms an interior circle?
As before, the circle will be interior if its center is more than one radius from the boundary. This means that the only circles with their center inside the $(1-2r)\times (1-2r)$ sub-square are interior.
These are the only diameters that form interior circles. However, there are other valid diameters to consider.
First of all, no center can be within a radius of the square’s boundary. This means that no centers inside the semi-circular curves of radius $r$ around each corner can form valid diameters (or interior circles). But we can have centers “under” these curves form valid diameters.
We can also have centers form valid diameters inside the four $r\times(1-2r)$ rectangles around the central square.
Drawing what we’ve figured out so far, we have:
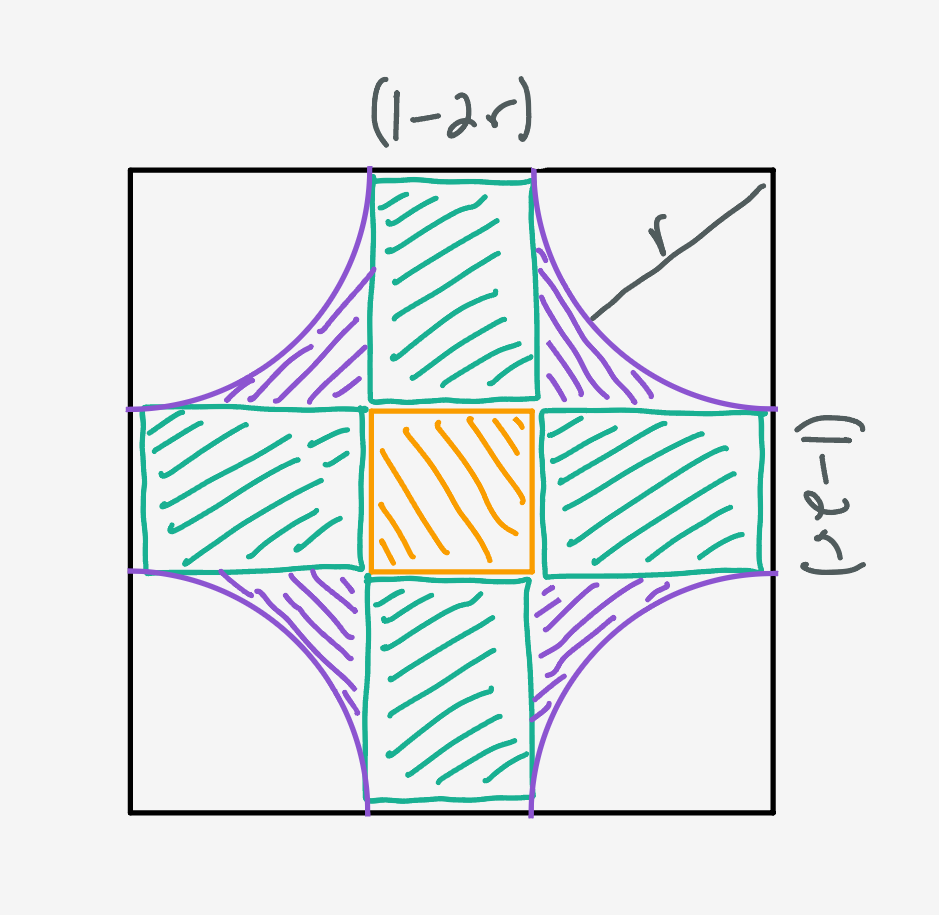
The probability that a valid diameter forms an interior circle is just the probability that a valid diameter’s center is inside the central $(1-2r)\times (1-2r)$ square:
\[P(\text{interior}\rvert r) = \frac{P(\text{square}\rvert \text{valid}, r)}{P(\text{square}\rvert \text{valid}, r) + 4P(\text{curve}\rvert \text{valid}, r) + 4P(\text{rectangle}\rvert \text{valid}, r)}.\]Easier to calculate is the probability that a diameter is valid inside a particular region. For example, we can rewrite $P(\text{square}\rvert\text{valid}, r)$ like
\[P(\text{square}\rvert\text{valid}, r) = \frac{P(\text{square, valid}\rvert r)}{P(\text{valid}\rvert r)}.\]With this, the probability of an interior circle becomes
\[P(\text{interior}\rvert r) = \frac{P(\text{square, valid} \rvert r)}{P(\text{square, valid} \rvert r) + 4P(\text{curve, valid} \rvert r) + 4P(\text{rectangle, valid} \rvert r)}.\]We know that $P(\text{square, valid}\rvert r) = (1-2r)^2,$ but we need to find $P(\text{curve, valid}\rvert r)$ and $P(\text{rectangle, valid}\rvert r).$
These probabilities are equal to the fraction of possible orientations that lead to valid diameters in each region:
\[\frac{\theta_\text{valid}}{\theta_\text{possible}}.\]Rectangular protuberance
The four protuberances are symmetric, and we’ll consider the right one for the purpose of this calculation.
Inside the right rectangular protuberance, we have a valid diameter so long as $x_c$ is further from the wall than $r\sin\theta.$
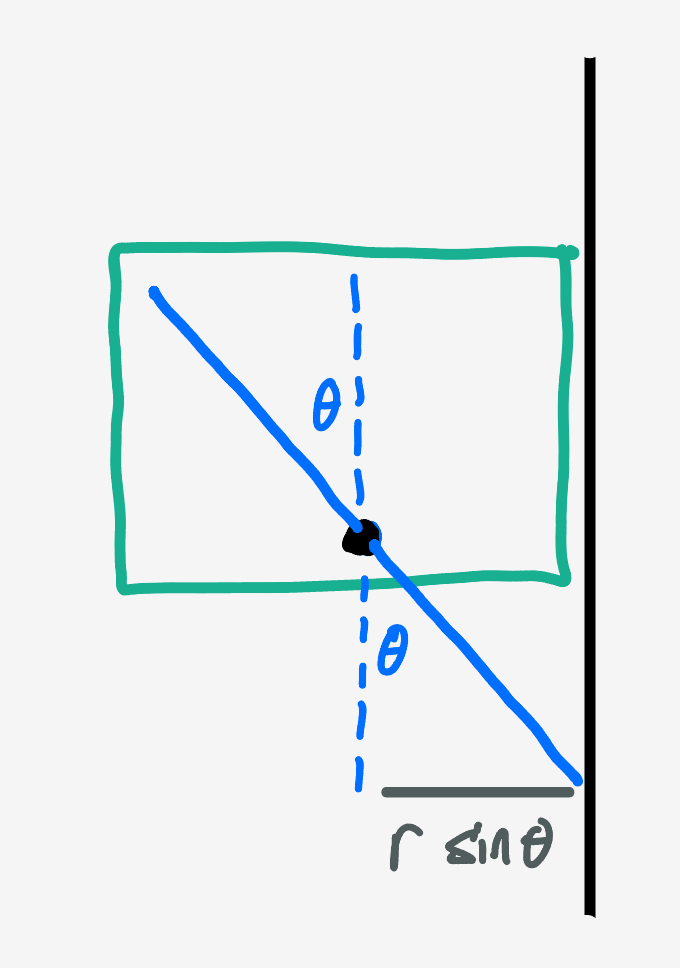
This defines a range of angles $(-\theta,\theta)$ that the diameter can have without crossing the wall. Solving $r\sin\theta = 1-x_c$ gives us $2\theta = 2\arcsin\left(\frac{1-x_c}{r}\right).$ Since the angle is chosen at random, the probability of a valid diameter is just
\[\begin{align} P(\text{rectangle, valid}\rvert x_c, y_c, r) &= \frac{2\theta}{\pi} \\ &= \frac{2}{\pi}\arcsin\left(\frac{1-x_c}{r}\right) \end{align}\]Adding up over all possible values of $x_c$ and $y_c,$ the probability of a valid diameter in the rectangle is
\[\begin{align} P(\text{rectangle, valid}\rvert r) &= (1-2r)\int\limits_{1-r}^1 dx_c\, P_\text{rect}(\text{valid}\rvert x_c) \\ &= (1-2r)\int\limits_{1-r}^1 dx_c\, \frac{2}{\pi}\arcsin\left(\frac{1-x_c}{r}\right) \\ &= \frac{(\pi-2)r(1-2r)}{\pi}. \end{align}\]Under the curve
When the center is in the region under the curve, the top and side of the square have distinct extreme angles. At the right wall, the diameter can tilt until $(1-x_c) = r\cos\theta_\text{right}.$ Likewise, at the top it can tilt until we have $(1-y_c) = r\cos\theta_\text{top}.$
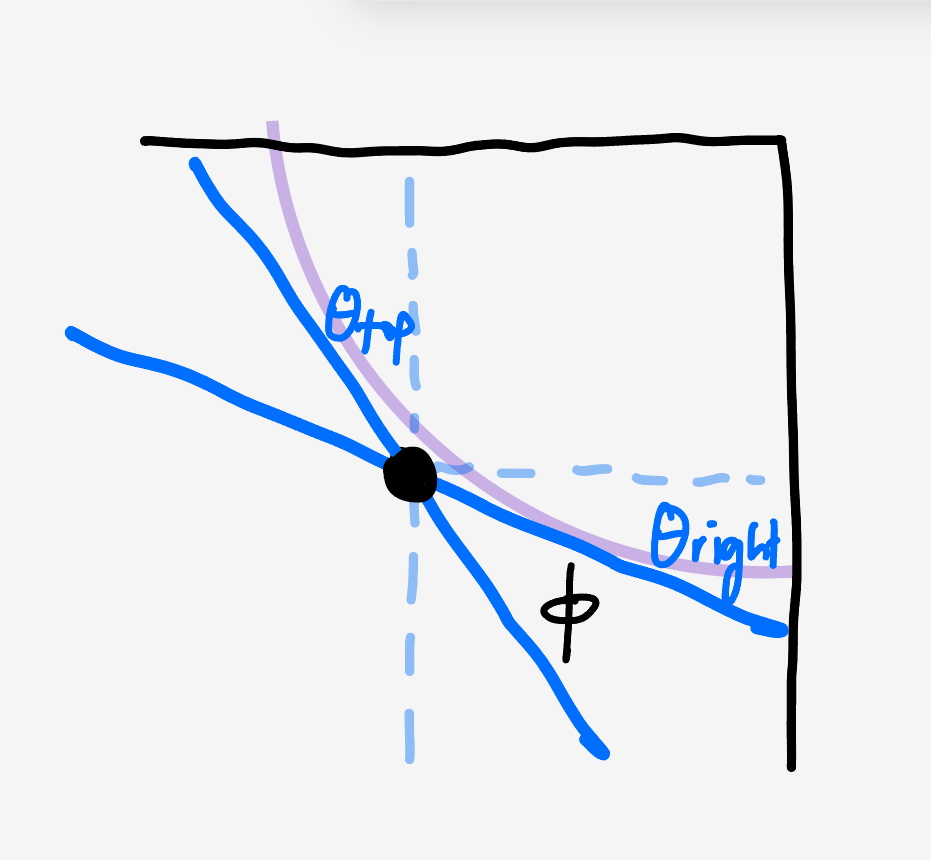
The angle the diameter can wiggle through is what’s left over:
\[\left(\frac12\pi - \theta_\text{right} - \theta_\text{top}\right).\]If we rotate the diameter so that one end is in the corner, there is a second band of feasible angles. Drawing the diagram, this has the same constraints we just went through.
So, the total feasible angle is
\[\theta_\text{curve} = 2\left(\frac12\pi - \theta_\text{right} - \theta_\text{top}\right).\]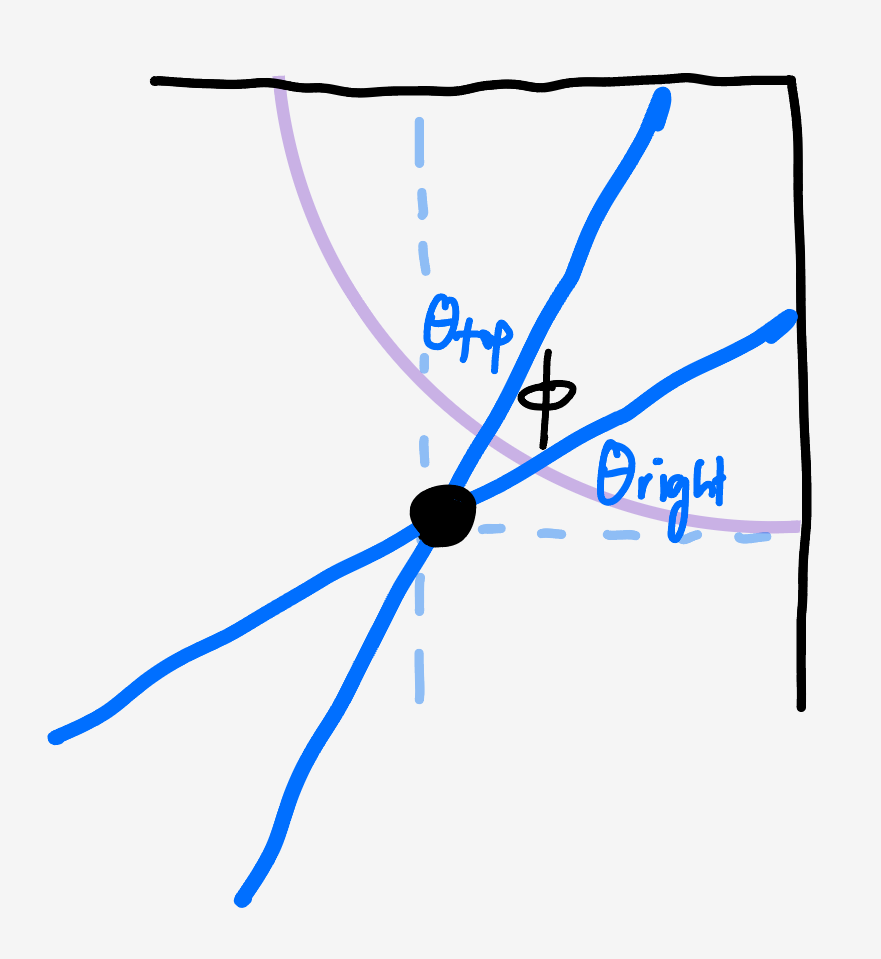
Solving the equations, this gives
\[P(\text{curve, valid}\rvert x_c,y_c, r) = \frac{1}{\pi}\left(\frac12\pi - \arccos\frac{1-x_c}{r} - \arccos\frac{1-y_c}{r}\right).\]Summing over all possible $(x_c,y_c)$ gets us
\[\begin{align} P(\text{curve, valid}\rvert r) &= \int\limits_{1-r}^1 dx_c\hskip{-0.65em}\int\limits_{1-r}^{1-\sqrt{r^2 - (x-1)^2}} \hskip{-0.7em}dy_c\, P_\text{curve}(\text{valid}\lvert x_c,y_c) \\ &= \frac{(\pi-3)r^2}{2\pi} \end{align}\]With these expressions in hand, we can plug them into the expression for $P(\text{interior}\rvert r),$ and after some simplification, get
\[P(\text{interior}\rvert r) = \frac{\pi(1-2r)^2}{\pi - 4r(2-r)}.\]So, we have
\[\begin{align} P(\text{interior}\rvert r)P(r) &= \frac{\pi(1-2r)^2}{\pi - 4r(2-r)} \cdot 8r\left(\pi - 4r(2-r)\right) \\ &= 8\pi r(1-2r)^2 \end{align}\]which is the same expression we found from the measurement argument.
So, the probability is again
\[\begin{align} P(\text{overlap}) &= 1-P(\text{interior}) \\ &= 1 - \frac{\pi}{6}. \end{align}\]What do we get for all this detailed work, beyond a testament to the self-consistency of our universe? We get detailed predictions for the probability distribution of the diameter’s center that can be compared to the empirical record.
Forming a heatmap from the expressions above, and building the same from a $N = 10^8$ round simulation, we find:
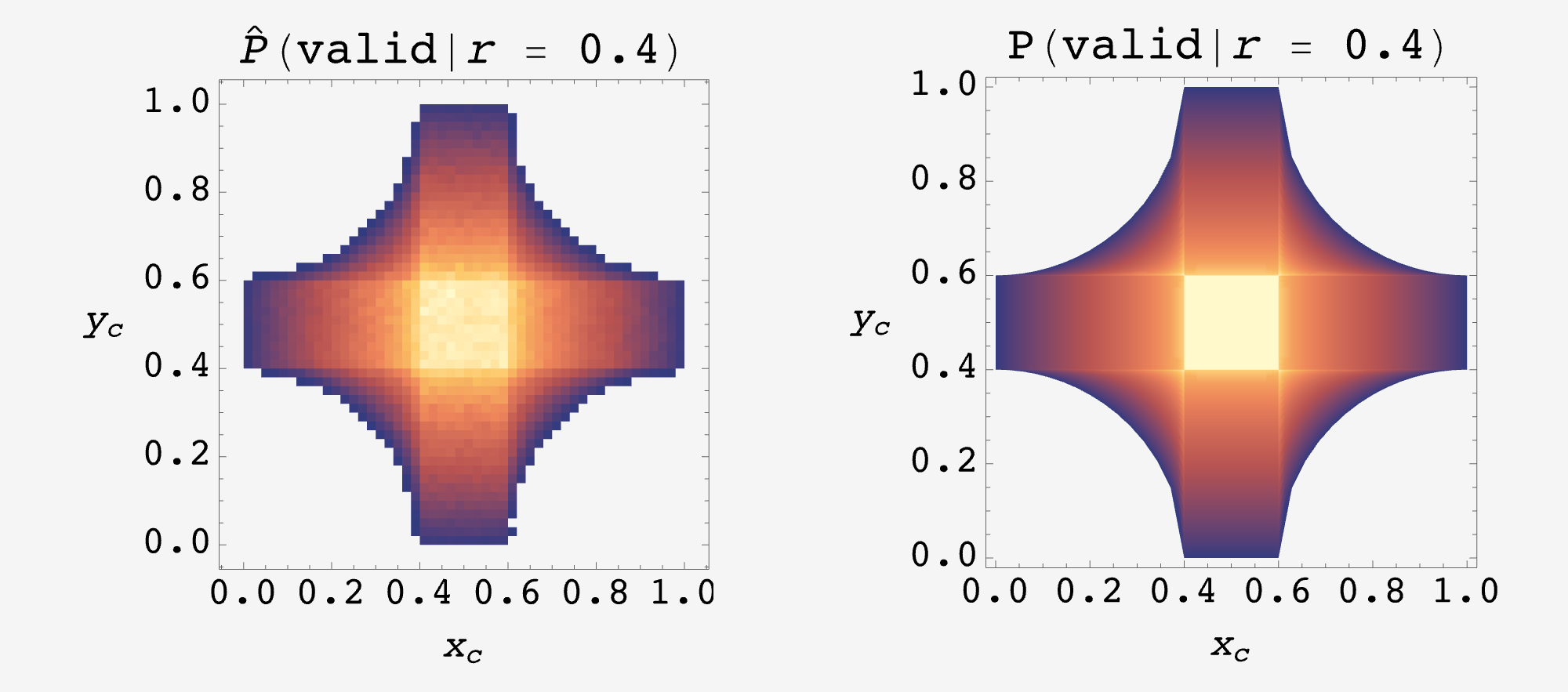
The empirical and analytical distributions, computed for $r=0.4.$