Question: A weaving loom set comes with a square with equally spaced hooks along each of its sides, as well as elastic bands that can be attached to the hooks.
Suppose a particular weaving loom has $N$ hooks on each side, evenly spaced from one corner to another (i.e., there are two hooks on the two corners and $(N−2)$ hooks between them). Let’s label the hooks along one side A1 through AN, the hooks on the next clockwise side $B_1$ through $B_N$ (with $A_N$ and $B_1$ denoting the same hook), the hooks on the third clockwise side $C_1$ through $C_N,$ and the hooks on the final side $D_1$ through $D_N.$
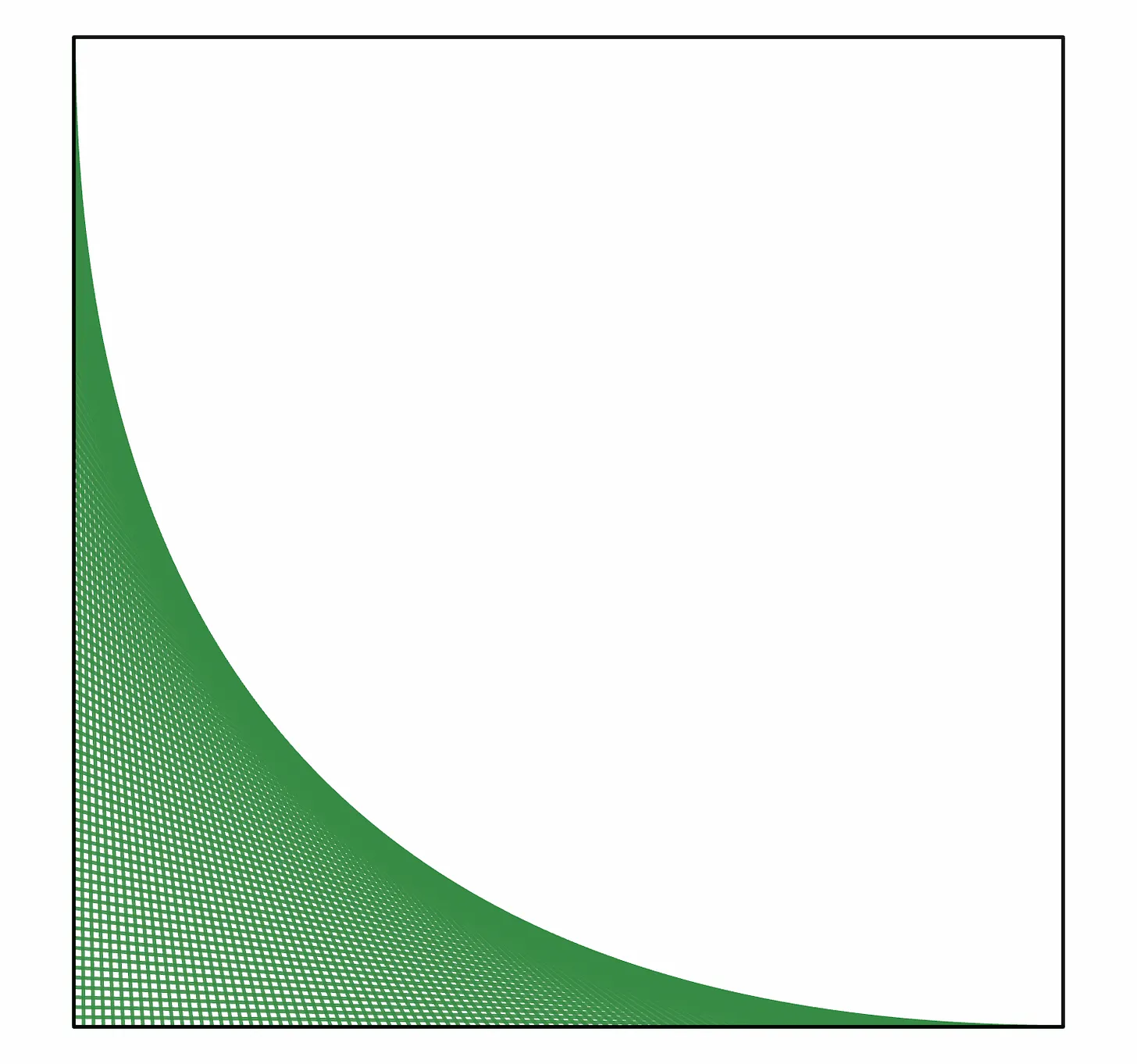
Next, let’s use a whole bunch of elastic bands to connect hooks $A_1$ and $B_1,$ $A_2$ and $B_2,$ $A_3$ and $B_3,$ and so on, up to $A_N$ and $B_N.$ When $N$ is $100,$ here’s what the loom looks like:
A square is shown. Points along the left edge are connected to points along the bottom edge, forming a mesh of green lines. The top right intersections of the mesh trace out a curve.
As $N$ increases, what is the shape of the curve formed by the edges of the bands? Your answer can be a single word or a mathematical equation.
Extra Credit
Let’s quadruple the number of bands placed on the weaving loom. In addition to the band connecting $A_1$ and $B_1,$ you also place bands connecting $B_1$ and $C_1,$ $C_1$ and $D_1,$ and $D_1$ and $A_1.$ You do this for all the sets of hooks from $1$ through $N,$ so that a total of $4N$ bands have been placed.
When $N$ is $100,$ here is what the loom looks like:
Similar to the mesh of the previous image, but now there are four sets of meshes, each formed by a pair of adjacent sides. In the middle is a white region that is not covered by any part of the four meshes.
As $N$ increases, what fraction of the loom’s area lies between the four sets of bands? In other words, what fraction of the square above does the central white region make up?
Solution
To get a picture of where the curve comes from, let’s draw the construction with a small number of divisions:
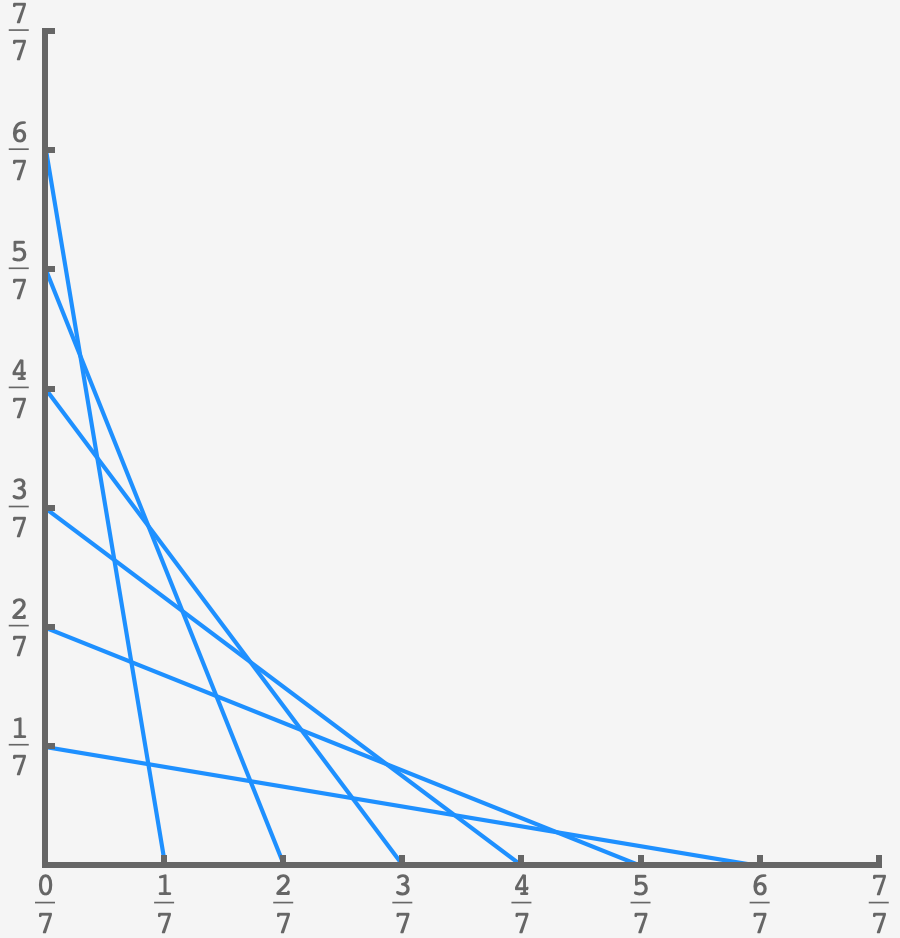
For example, the first line has the relationship $y = \frac{(1 - 1/N)}{1/N}(1/N-x).$
In general, the $j^\text{th}$ line is
\[y_j = \frac{(1-j/N)}{j/N}(j/N-x).\]Each point on the frontier curve is the intersection of two consecutive lines:
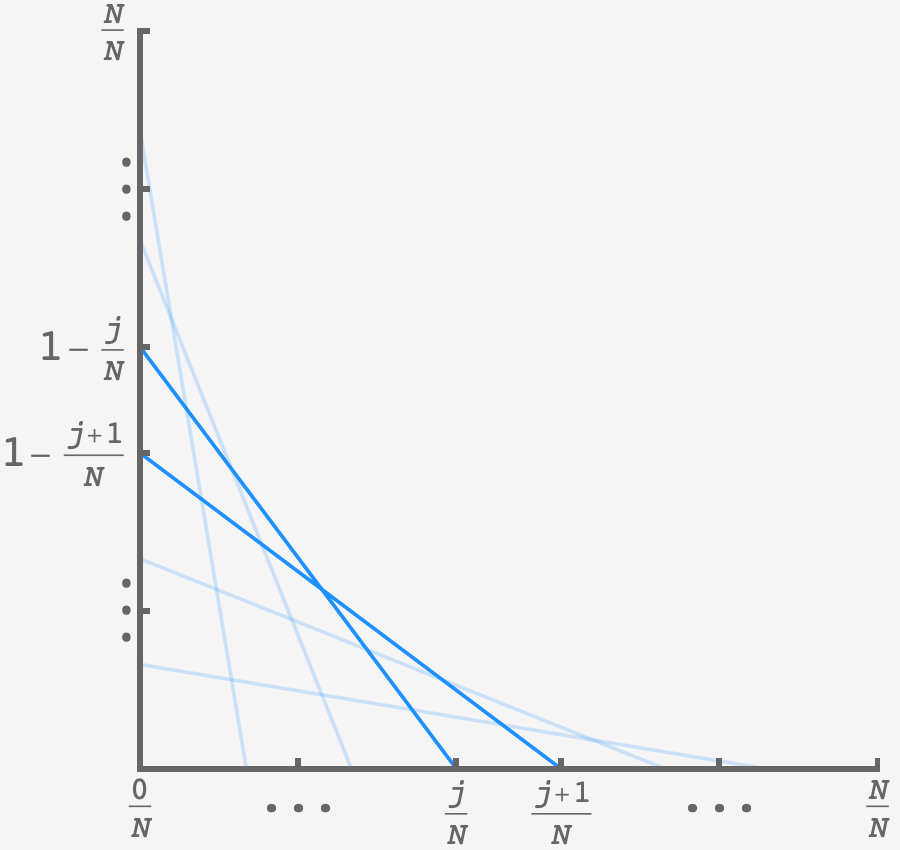
These intersections occur when $y_j(x) = y_{j+1}(x)$ or
\[\frac{1-j/N}{j/N}(j/N-x) = \frac{1-(j+1)/N}{(j+1)/N}\left[(j+1)/N-x\right].\]Solving for $x$ in terms of $j$ gives $x = j(j+1)/N^2.$ Taking the limit as $N$ goes to infinity and letting $j/N = t$, we get
\[x = t^2\]We can also use this to get $y$ in terms of $t$:
\[y = (1-t)^2,\]which gives us the frontier curve in parametric form. Plotting this along side the lines, we see that it is indeed the shape of the frontier:
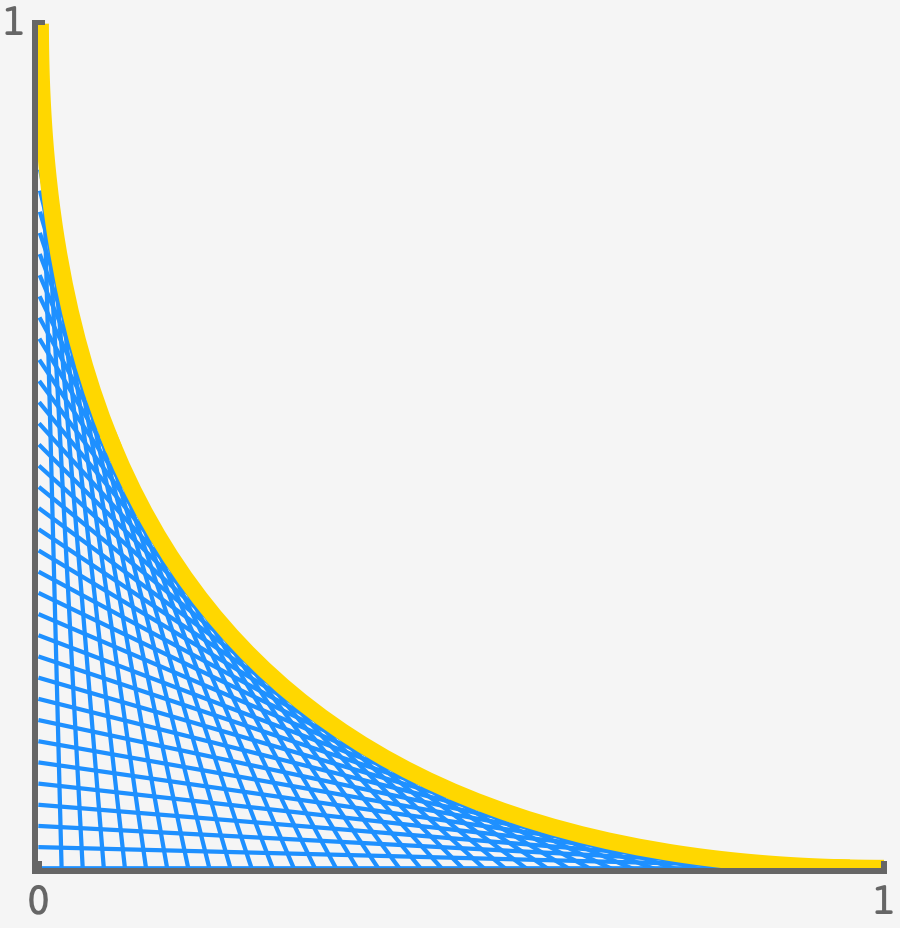
Unmasking the curve
But what kind of shape is it?
If we take the square root of $x$ and $y,$ we see that $\sqrt{x} + \sqrt{y} = 1.$ That’s nice but is not a common form.
Since it’s symmetric about the line $y=x,$ it may be helpful to look at it in the tilted coordinate system $(x-y, x+y).$
Going along with this, we see that
\[\begin{align} x-y &= 2t - 1 \\ x+y &= 2t^2 - 2t + 1. \end{align}\]This reveals that $(x-y)^2$ is twice $(x+y)$ minus $1.$
In other words, if we let $z = x+y$ and $w = x-y,$ we have
\[z = \frac{w^2 + 1}{2},\]which is an ordinary parabola in the tilted coordinate system.
Finding the area
By the symmetry of the construction we can focus on one of the four equivalent sections which consists of a rectangle from the origin to the point where $y = \frac12$ plus the area under the curve from that point to $x=\frac12.$
Setting $y = (1-t)^2 = 1/2,$ we get $t_* = 1 - \sqrt{\frac12}.$
This makes the total area covered by the threads
\[\begin{align} A &= 4\left[x_* y_* + \int\limits_\text{left edge}^\text{right edge} \text{d}x\, y(x)\right] \\ &= 4\left[x(t_*)y(t_*) + \int\limits_{t_*}^{\sqrt{1/2}} \text{d}t\, 2t\, (1-t)^2\right] \\ &= 4\left[\frac{1}{2} \left(1-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{3}-\frac{1}{3 \sqrt{2}}\right] \\ &\approx 0.562097\ldots \end{align}\]Subtracting this area from the enclosing square, the white region occupies approximately $43.79\%$ of the square.