Question: The astronomers of Planet Xiddler are back in action! Unfortunately, this time they have used their telescopes to spot an armada of hostile alien warships on a direct course for Xiddler. The armada will be arriving in exactly $100$ days. (Recall that, like Earth, there are 24 hours in a Xiddler day.)
Fortunately, Xiddler’s engineers have just completed construction of the planet’s first assembler, which is capable of producing any object. An assembler can be used to build a space fighter to defend the planet, which takes one hour to produce. An assembler can also be used to build another assembler (which, in turn, can build other space fighters or assemblers). However, building an assembler is more time-consuming, requiring six whole days. Also, you cannot use multiple assemblers to build one space fighter or assembler in a shorter period of time.
What is the greatest number of space fighters the Xiddlerian fleet can have when the alien armada arrives?
Solution
Whether we have $1$ assembler, or $1$ billion of them, the decision of what to do with each one is independent of the others.
The tradeoff between assemblers and spaceships is this:
- if we invest the time to make another assembler, then we can make spaceships twice as fast, but
- while the assembler was getting made, we could have built $144$ spaceships
So, if we have a lot of time, we should use some of it to make assemblers. If we have a little time, we should forget assemblers and just build spaceships.
We can quantify this tradeoff to find the tipping point.
Calculation
Suppose we have $h$ hours left.
If we set an assembler to make an assembler, and then make starships with the time left over, we’ll use $144$ hours to make the second, and $(h-144)$ hours to make starships (at double the rate), whereas if we let the original start making starships, it would have made $h$ of them:
\[2(h-144) = h.\]The two sides are equal when $h=288.$ So, if the time remaining is less than $288$ hours, we should devote all assemblers to make starships. Otherwise we should have them make assemblers, and switch to $100\%$ starship production the first time we end an assembler build with less than $288$ hours remaining.
If we don’t have at least $288$ hours ($12$ days) to play with, then there isn’t enough time for the greater number of assemblers to outweigh the foregone starship production.
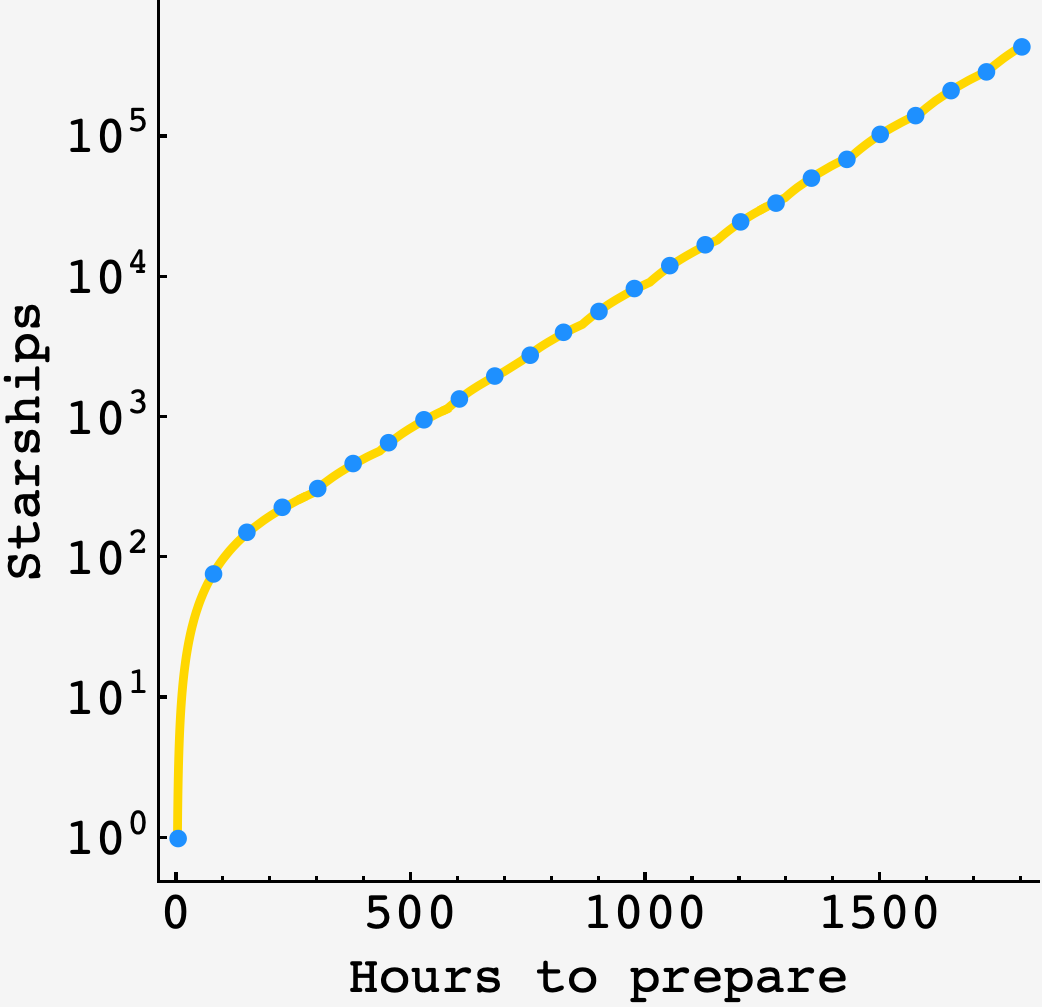
So, with $2400$ hours to work with, we should make assemblers for $\lfloor 2400/144 - 1\rfloor = 15$ cycles, after which we’ll have $32,768$ assemblers, and $10$ days to starship production.
This will leave us with
\[\begin{align} S(2400) &= 240 \times 2^{15} \\ &= 7,864,320 \end{align}\]starships.
In general, this production plan will build
\[S(h) = (h-144t)2^t\]starships, where $t=\lfloor \frac{h}{144}-1\rfloor.$
Optimal policy
We can check the intution here by finding the maximum with dynamic programming. If we have $H$ hours left and $A$ assemblers, then we have the choice to apportion them to spaceships or assemblers any way we like. If we have less then $144$ hours left, then we can’t finish any new assemblers, and we should just devote the assemblers we have to starship production.
Mathematically, this is
\[S(H,A) = \begin{cases} H\times A & H\leq 144 \\ \max\limits_{0\leq x\leq A} S(H-144,2x) + (A-x) + S(H-1, A-x) & \text{otherwise} \end{cases}\]Coding this up, it matches exactly with the analytic prediction: