Question: Every Christmas, Gary’s family has a gift exchange. And every year, there is a big fight over how much folks should spend on the gifts. This year, they decided to pair up. So if Virginia gives Justin a gift, then Justin gives Virginia a gift. This way, while there will still be arguments, only two people will be involved in each argument.
There are $20$ people in the gift exchange. In the first round, everyone writes down the name of a random person (other than themselves) and the names go in a hat. Then if two people randomly pick each other’s names out of that hat, they will exchange gifts, and they no longer participate in the drawing. The remaining family members go on to round two. Again, they write down the name of anyone left, and again, any two people who pick each other exchange gifts.
This continues until everyone is paired up. And yes, if exactly two people remain, they still go through the process of selecting each other, even though they know who their partner will be.
On average, what is the expected number of rounds until everyone is paired up?
Solution
This problem is hard because connections formed by early draws influence the potential pairs for later draws. Things are simpler if we work in the ensemble of all possible series of draws.
From this perspective, each round of $n$ people consists of $\frac12n$ independent potential pairs. To find the expected number of pairs formed in a round, we can calculate the probability that any given pair forms successfully and multiply it by the number of possible pairs.
First of all, with two players, the expected number of pairs formed is $P_2 = \frac12.$ Either the first person draws the other person’s name, or they don’t.
With more players we have to do more careful accounting, but to get the intuition going let’s do the $N=4$ case playing fast and loose.
Intuitive sketch
With four players, there are two potential pairs. Since the names are (at the beginning) uniformly probable, the chance that the first person of a pair doesn’t draw their own name is $\frac34$ (this part is exact). Similarly, the probability that the first person’s draw draws their name in return is approximately $\frac14$ (this piece is slightly wrong). So, the expected number of pairs per round is
\[P_4 \approx 2\times\frac34\times\frac14 = \frac38 = 0.375\]Careful argument
Again, there is a $\frac34$ probability that the first person does not draw their own name.
However, the first person’s draw affects the probability that their name, “1”, is in the bag. Overall, the expected number of pairs formed in a $4$-person round is
\[\begin{align} P_4 =\ &\text{number of potential pairs} \times \\ &P(\text{first person draws someone else}) \\ & P(\text{second person draws first person}) \end{align}\]and we have to find the last term. This chance depends on whether the name Player 1 drew was one that they submitted or not.
Given that the first person didn’t draw their own name, “1”, there’s a $\frac13$ chance that they submitted the name they drew. In that case, the second person will be drawing from three names submitted by the other three people, which will have probability $\frac39$ of being a “1”.
Likewise, if the first person did not submit the name they drew (probability $\frac23$), then the second player will be drawing from three names submitted by the first person (who can’t contribute their own name to the hat) and the other two players (who can contribute the first person’s name to the hat) which will have a $\frac29$ probability of being the first person’s name, “1”.
Putting it together, the chance that the second person draws the first person’s name (given that the first person did not draw their own name) is
\[\begin{align} P(\text{second person draws first person}) &= \frac13\times\frac39 + \frac23\times\frac29 \\ &= \frac{7}{27} \end{align}\]This makes the expected number of pairs in a round with $4$ players equal to
\[P_4 = 2\times\frac34\times\frac{7}{27} = \frac{7}{18} \approx 0.3888\ldots\]In general, for $n$ players, the expected number of pairs in a round of $n$ players is
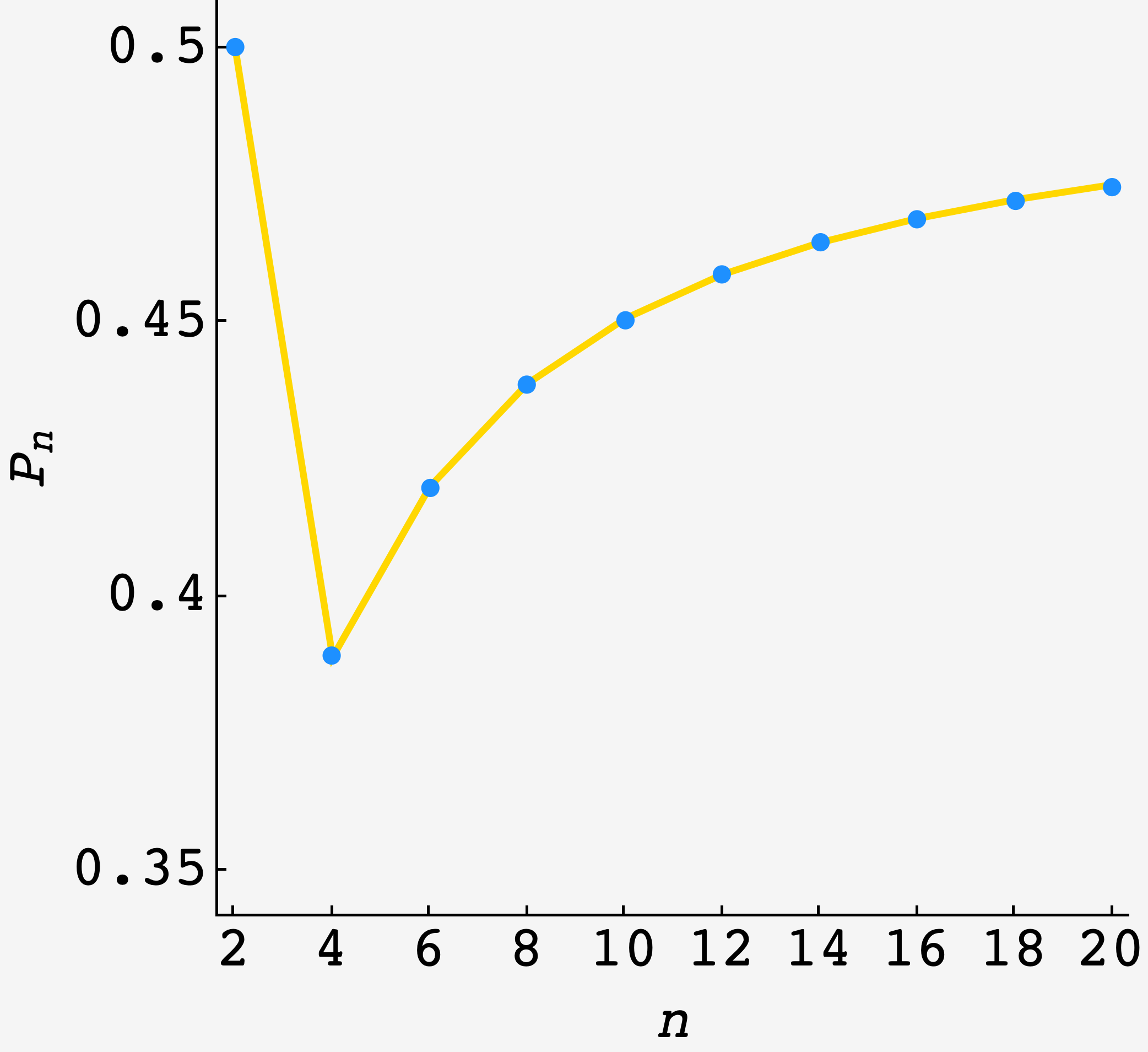
\[\begin{align} P_n &= \frac{n}{2}\frac{n-1}{n}\left[\frac{1}{n-1}\frac{n-1}{(n-1)^2} + \frac{n-2}{n-1}\frac{n-2}{(n-1)^2}\right] \\ &=\frac{n}{2}\frac{n-1}{n}\frac{(n-3)n+3}{(n-1)^3} \\ &= \frac{(n-3)n + 3}{2(n-1)^2}. \end{align}\]Comparing the prediction (gold) with a high-$N$ simulation for $P_n,$ we see good agreement
Expected waiting time
Now, we’re going to make a simplifying assumption. Rather than track the potential for, e.g., multiple pairs forming in a single round, we’re just going to find the expected waiting time for a pair to form at each stage, and add up those waiting times to find the total.
At each stage of the game, we should expect to wait $P_n^{-1} = \frac{2(n-1)^2}{(n-3)n + 3}$ rounds for a pair to form, so the expected duration of the game is approximately
\[\begin{align} \langle T_{20}\rangle &\approx P_2^{-1} + P_4^{-1} + \ldots + P_{20}^{-1} \\ &= \sum\limits_{j=\frac12 n=1}^{10} P_{2j}^{-1} \\ &= 2\sum\limits_{j=\frac12 n=1}^{10} \frac{(2j-1)^2}{4j^2 - 6j + 3} \\ &= 2\sum\limits_{j=\frac12 n=1}^{10} \left[1 + \frac{2j - 2}{4j^2 - 6j + 3}\right] \\ &= 20 + 2\sum\limits_{j=\frac12 n=1}^{10} \frac{2j - 2}{4j^2 - 6j + 3} \\ &\approx 22.1385\ldots \end{align}\]Running an $N = 10^6$ round simulation produces $\hat{T}_{20} \approx 22.1104.$
General waiting time
Generalizing the last calculation, the waiting time for an $n$ guest game is
\[\langle T_n\rangle \approx n + 2\sum\limits_{j=1}^{\frac12 n}\frac{2j-2}{4j^2-6j+3}.\]Plotting the prediction (gold curve) against a high-$N$ simulation (blue points), we see good agreement
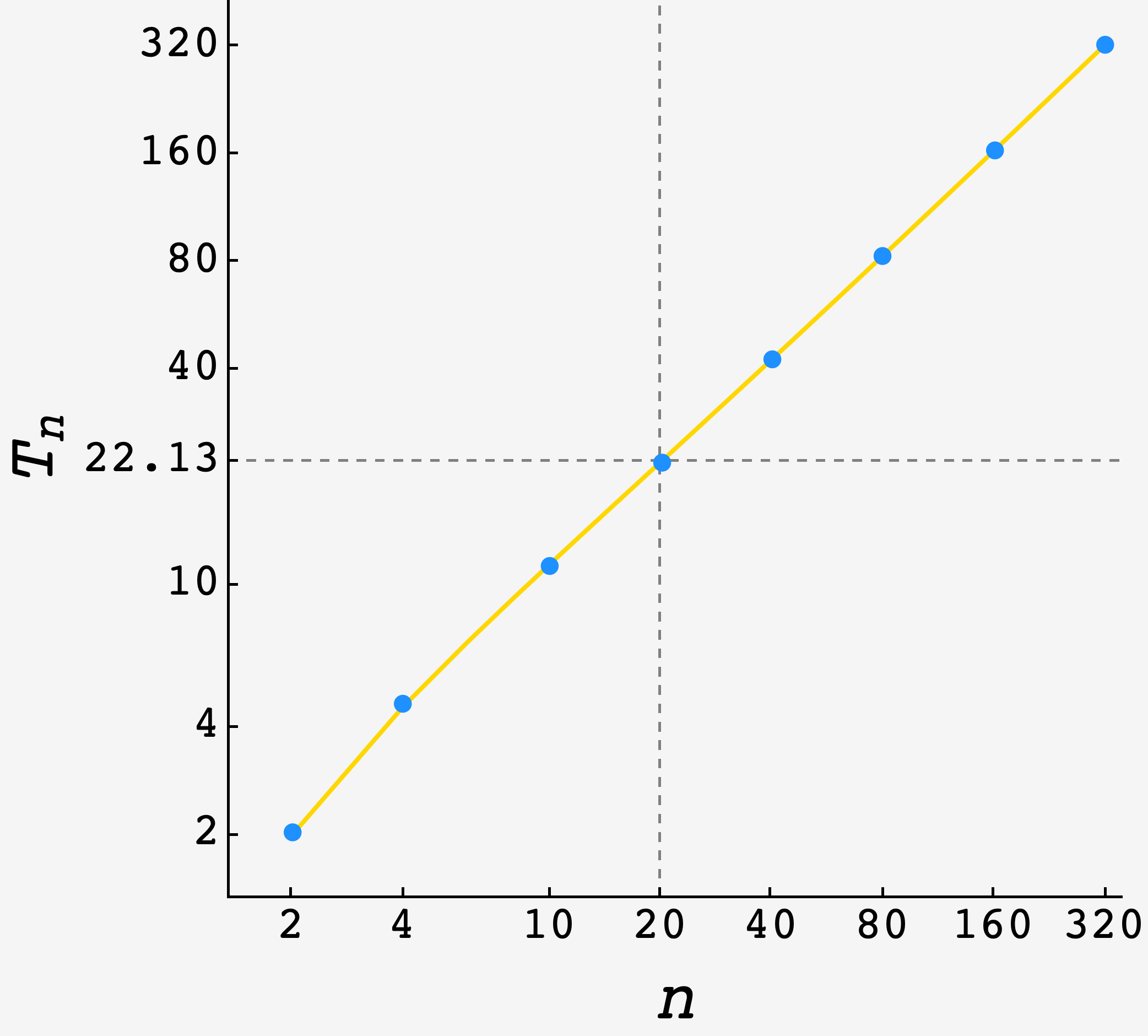
Empirically, we can see that the expected waiting time is basically a linear function in $n.$ This is because the summation term grows sublinearly in $n$ (practically $\approx O(1)$), so the waiting time is dominated by the bare number of guests.