Question: From the fantastical land of Central Earth comes a physics riddle that will break down your doors:
In an effort to break open the gates of the city Tinas Mirith, an army of orcs first tried using a battering ram, but to no avail. They next erected a $100$-foot pole with a very massive weight at the top (i.e., the weight is much, much heavier than the rest of the pole). The pole is also anchored at the bottom, so that as the weight falls the entire pole rotates around its bottom without slipping.
How far away should the orcs position the vertical pole from the gates so that when the weight comes crashing down on the gates, its horizontal speed is as great as possible?
Solution
Throughout the hammer’s fall, energy is conserved. When the hammer makes angle $\phi$ with the ground, the energy is
\[E = \frac12 MV^2 + Mg\ell\sin\phi.\]Initially, the hammer is standing still and straight which lets us solve for $V(\phi):$
\[V(\phi) = \sqrt{2g\ell\left(1-\sin\phi\right)}.\]We care about the horizontal component of the hammer’s velocity, $V_x(\phi) = V(\phi)\sin\phi.$
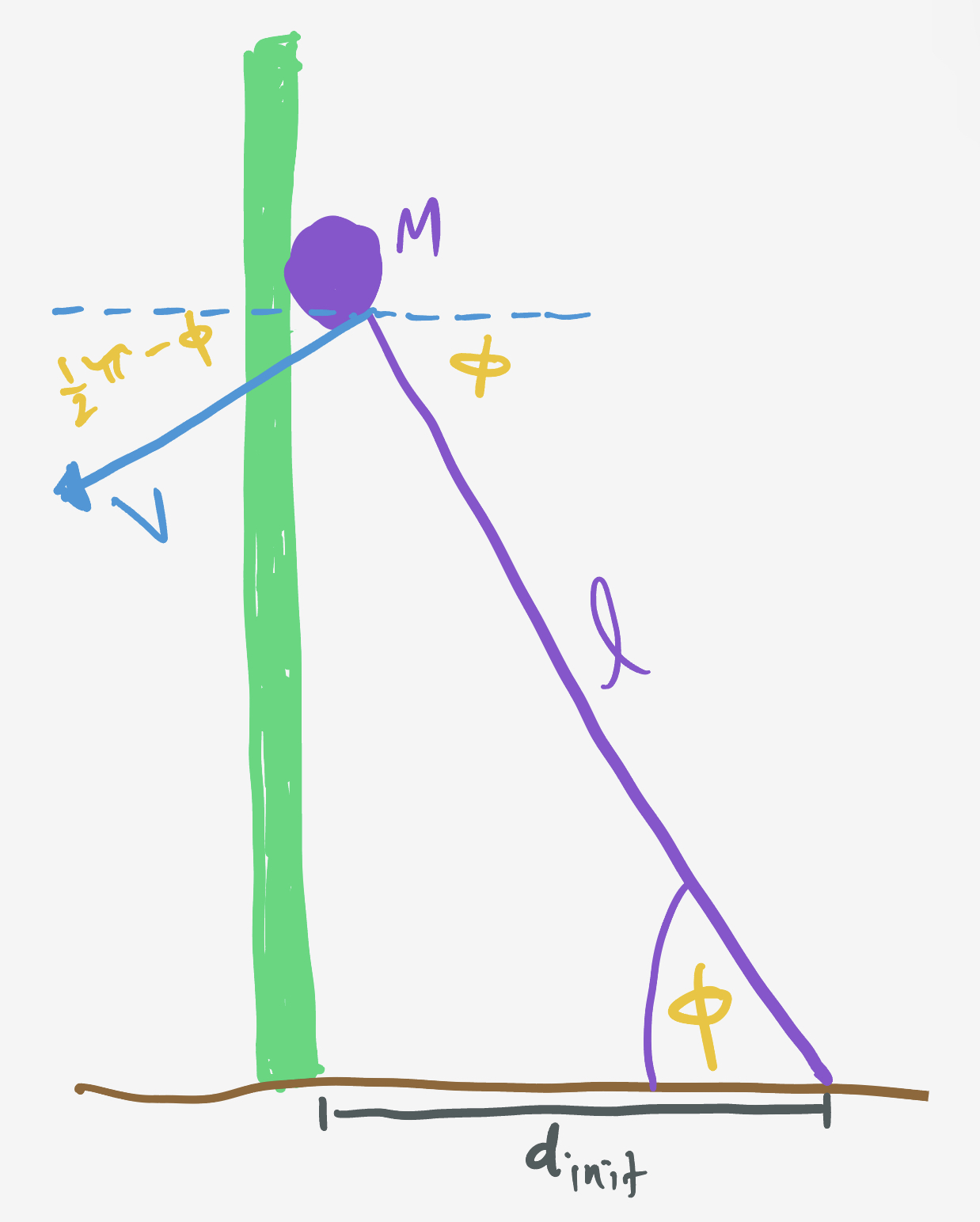
We want to maximize this, and it’s easier to do that working with the square $V_x(\phi)^2:$
\[V_x(\phi)^2 = \sin^2\phi\left(1-\sin\phi\right).\]Taking the derivative and setting it to zero, we get
\[2\sin\phi\cos\phi = 3\sin^2\phi\cos\phi,\]so that $V_x(\phi)$ is maximized when $\sin\phi = \frac23.$
The hammer hits the door when $\ell\cos\phi = d_\text{init},$ so we should place the hammer $\boxed{d_\text{init} = \ell\sqrt{1-2^2/3^2}}$ away from the door.
If we do that, then the hammer will hit the door with speed $V_x = \frac23\sqrt{\frac23 g\ell} \approx 9.41\text{ m/s}$ (where $\ell=100\text{ ft}\approx 30.48\text{ m}$).