Question: It’s peak fall foliage season in Riddler Nation, where the trees change color in a rather particular way. Each tree independently begins changing color at a random time between the autumnal equinox and the winter solstice. Then, at a random later time for each tree — between when that tree’s leaves began changing color and the winter solstice — the leaves of that tree will all fall off at once.
At a certain time of year, the fraction of trees with changing leaves will peak. What is this maximal fraction?
Solution
The leaves can start changing at any time $t_\text{c}$ up until $t,$ so the chance that a tree will have its fall colors at time $t$, $P(\text{color at }t),$ is
\[P(\text{color at }t) = \int\limits_0^t\text{d}t_\text{c}\ P(\text{color at }t\rvert t_\text{c})P(t_\text{c}).\]Given $t_\text{c},$ the probability that the tree is colored at time $t$ is zero if $t_\text{c}$ hasn’t happened yet, otherwise there is chance $(T-t)/(T-t_\text{c})$ that the leaves fall after time $t:$
\[P(\text{color at }t\rvert t_\text{c}) = \begin{cases} \dfrac{T-t}{T-t_\text{c}} & t \geq t_\text{c} \\ 0 & t < t_\text{c} \end{cases}.\]Putting it all together, the probability to see leaves at time $t$ is
\[\begin{align} P(\text{color at }t) &= \int\limits_0^t\text{d}t_\text{c}\dfrac{T-t}{T-t_\text{c}}\dfrac{1}{T} \\ &= \dfrac{T-t}{T}\log\dfrac{T}{T-t}. \end{align}\]Changing variables to $t^\prime = t/T,$ we have
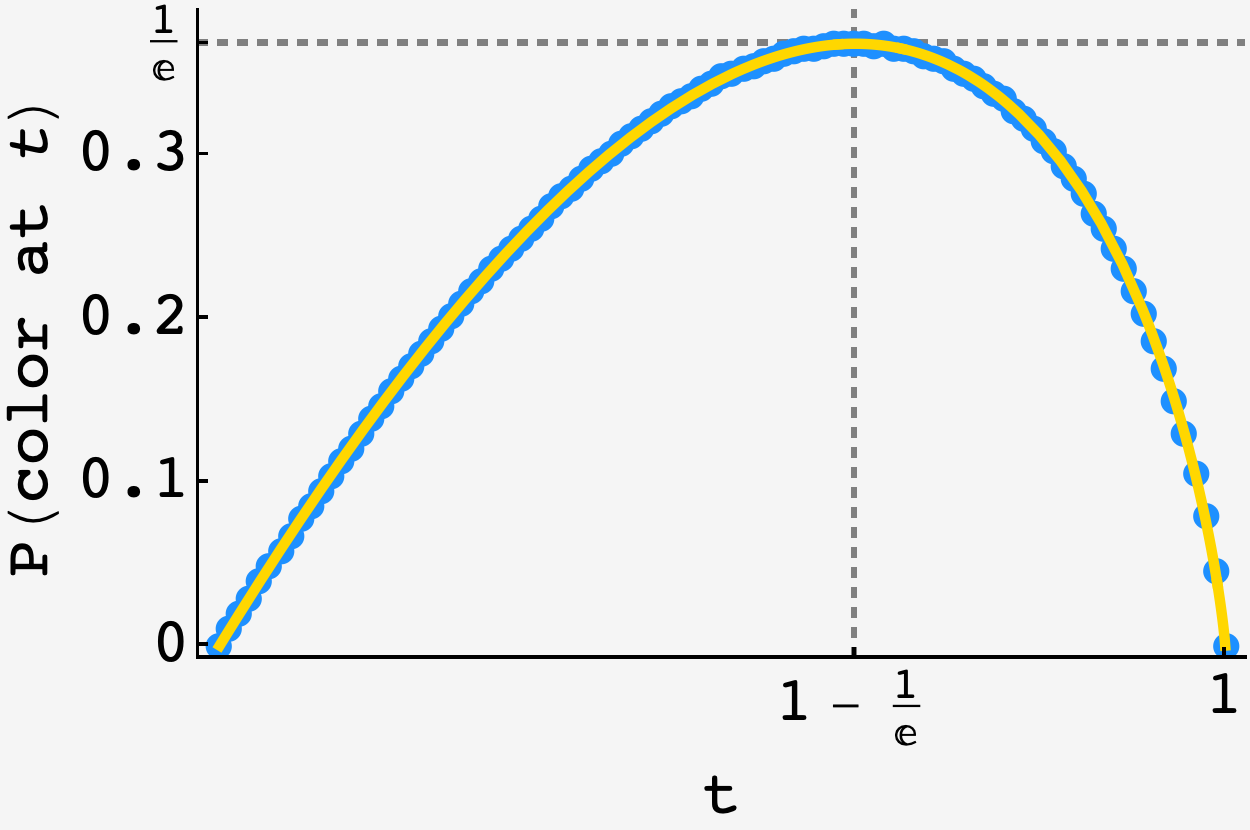
\[-(1-t^\prime)\log (1-t^\prime),\]which is maximized when $\log (1-t^\prime)=-1$ i.e. at $t^\prime=1-1/e,$ when the probability to see leaves is $1/e \approx 0.3679$
Plotting the prediction against an $N=10^6$ round simulation, it looks pretty good: