Question: Graydon is about to depart on a boating expedition that seeks to catch footage of the rare aquatic creature, F. Riddlerius. Every day he is away, he will send a hand-written letter to his new best friend, David Hacker. But if Graydon still has not spotted the creature after $N$ days (where $N$ is some very, very large number), he will return home.
Knowing the value of $N,$ Graydon confides to David there is only a $50%$ chance of the expedition ending in success before the $N$ days have passed. But as soon as any footage is collected, he will immediately return home (after sending a letter that day, of course).
On average, for what fraction of the $N$ days should David expect to receive a letter?
Solution
The number of letters David expects is equal to
\[\langle L\rangle = \frac12\langle L\rvert\text{monster by day }N\rangle + \frac12\langle L\rvert\text{no monster by day }N\rangle,\]the average of the expected number of letters received when the monster is seen by day $N$ and the expected number of letters received when the monster is not seen by day $N.$
No cutoff
If Graydon didn’t put a cutoff on the number of days he’s willing to wait, then David would expect to receive $\langle L\rangle_\text{no cutoff} = 1/p$ letters altogether.
Likewise, $\langle L\rvert\text{no monster by day }N\rangle_\text{no cutoff} = N + 1/p,$ since our fortunes after day $N$ are not effected by our efforts before day $N.$
Yes cutoff
When there’s a cutoff, $\langle L\rvert\text{no monster by day }N\rangle_\text{cutoff}$ is equal to $N,$ the number of letters sent by the time Graydon gives up.
Putting it together
Whether or not there’s a cutoff, the value of $\langle L\rvert\text{monster by day }N\rangle$ is the same. The no-cutoff case shows that
\[\langle L\rvert\text{monster by day }N\rangle = \frac{1}{p} - N.\]So, when Graydon has a cutoff, the expected number of letters is
\[\begin{align} \langle L\rangle_\text{cutoff} &= \frac12\langle L\rvert\text{monster by day }N\rangle + \frac12\langle L\rvert\text{no monster by day $N$}\rangle_\text{cutoff} \\ &= \frac12 \left(\frac1p - N\right) + \frac12 N \\ &= \dfrac{1}{2p} \end{align}\]Now, since there’s just a $50\%$ chance to see the monster by day $N,$ we can set $(1-p)^N = 1/2$ and get $p = 1 - 2^{-1/N}.$
Then, the fraction of days with a letter is
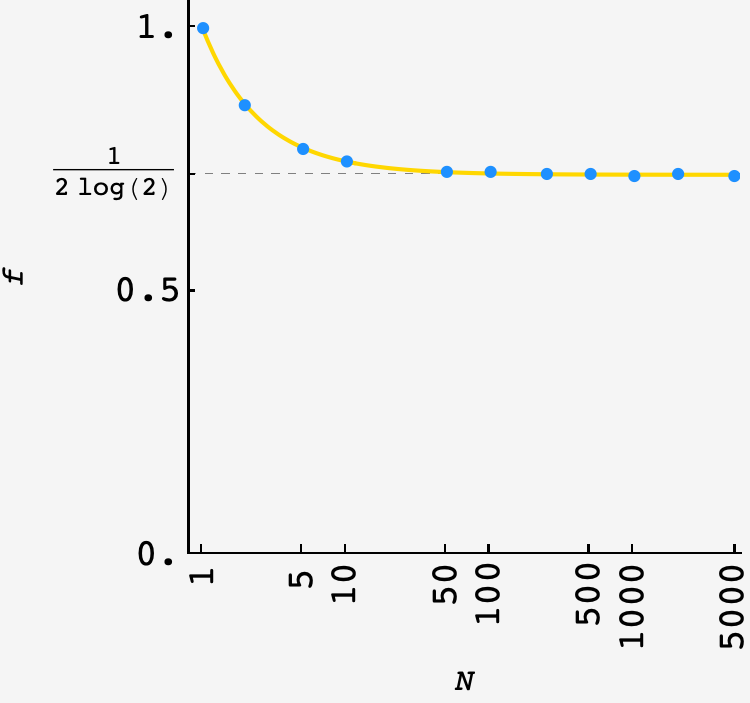
\[f = \dfrac{\langle L\rangle_\text{cutoff}}{N} = \dfrac{1}{2N}\dfrac{1}{1-2^{-1/N}}.\]Writing $2^{-1/N}$ as $e^{-\frac1N \log{2}}$ and expanding to first order, we get
\[\begin{align} f &= \dfrac{1}{2N}\dfrac{1}{1-(1 - \frac1N \log{2})} \\ &= \frac{1}{2\log 2} \end{align}\]so that, for big $N,$ David gets a letter on $1$ out of every $2\log 2$ of the $N$ days, or $\approx72.1\%$ of the time.
Plotting the prediction (gold) against a $10^6$ round simulation (blue), this seems pretty good: