Sock wash

Question: In my laundry basket, I have 14 pairs of socks that I need to pair up. To do this, I use a chair that can fit nine socks, at most. I randomly draw one clean sock at a time from the basket. If its matching counterpart is not already on the chair, then I place it in one of the nine spots. But if its counterpart is already on the chair, then I remove it from the chair (making that spot once again unoccupied) and place the folded pair in my drawer.

What is the probability I can fold all 14 pairs without ever running out of room on my chair?

Extra credit: What if I change the number of pairs of socks I own, as well as the number of socks that can fit on my chair?

(FiveThirtyEight)

Solution

There are three relevant locations for socks: in the basket, on the chair, or in the drawer.

When socks pair up and enter the drawer, we don’t care about them anymore because they can’t increase the number of unpaired socks on the chair. Also, the number of unpaired socks on the chair is equal to the number of unpaired socks in the basket.

So, we can uniquely describe the state of the system by tracking the number of single socks on the chair $s,$ and the number of doubles in the basket $d.$

At each step, two things can happen:

• we grab a member of a double in the basket and put it on the chair, with probability $2d/(s+2d),$ or
• we grab a single in the basket and pair it with its partner on the chair, with probability $s/(s+2d).$

In the first case, a new singleton is created $s \rightarrow (s+1)$ and an existing double is annihilated $d\rightarrow (d-1).$ In the second case a singleton is annihilated $s\rightarrow (s-1).$

Putting this all together, and calling the probability that the state $(s,d)$ leads to an overloaded chair $P(s,d),$ we get

The “base case” is that $P(10,d) = 1$ and $P(s,d) = 0$ whenever $s + d \leq 10$ (because it doesn’t have enough ingredients to make an overloaded chair).

Running the recursion shows that $P(0,14) = \frac{15627431}{22309287} \approx 0.70049.$

With the recursion in hand, we can vary the chair capacity $T$ relative to the number of pairs $N.$ Evidently, it shows sigmoid behavior, with no probability up until a transition point, after which it plateaus to $1$.

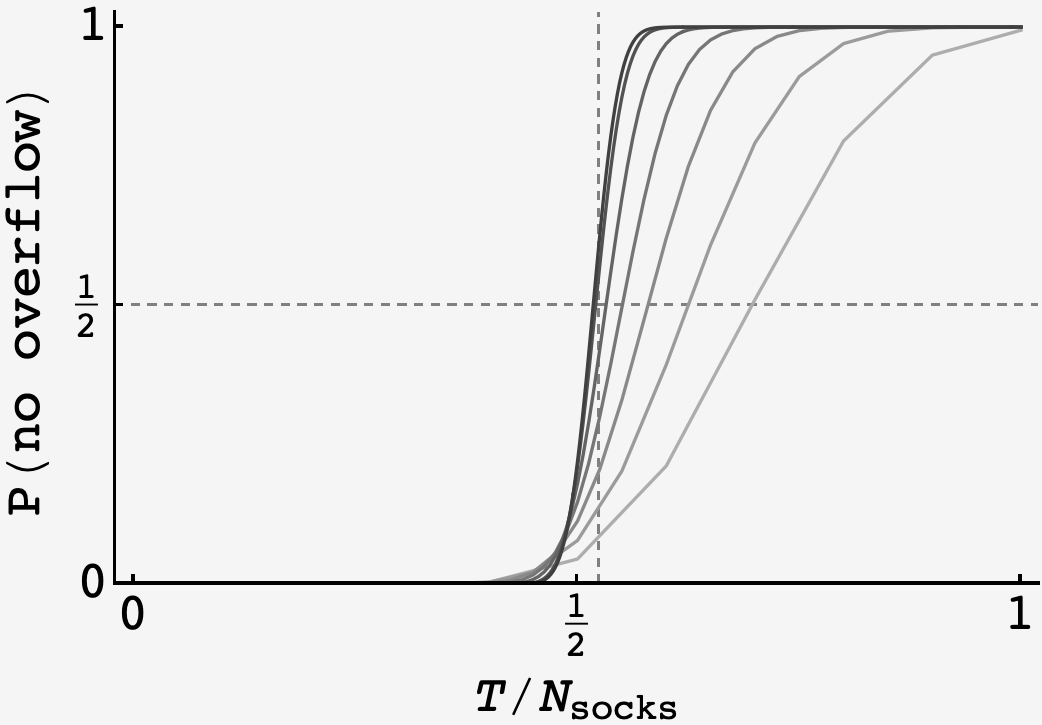
A plot of $P(\text{no overload})$ vs $T/N$ as $N$ varies from $10$ (light gray) up to $320$ (black).

Running $N$ up, we see that the sigmoid behavior persists, but the transition gets sharper, and the halfway induction point gets smaller.

Plotting the halfway induction value of $T/N$ for increasing $N,$ it appears to approach a limit that may remain above the intuitive limit of $1/2.$

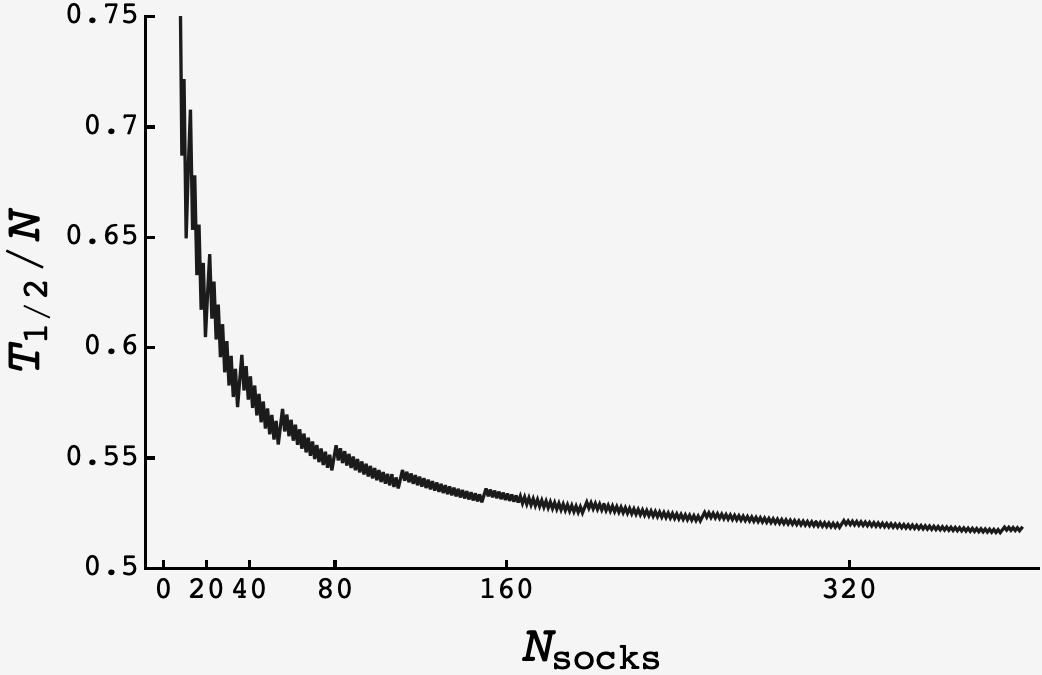
However, a better analytic approach or more computation time would be needed to weigh in with conviction.