Colorful balls

Question: You have an urn with an equal number of red balls and blue balls, but you have no information about what that number might be. You draw 19 balls at random, without replacement, and you get eight red balls and 11 blue balls. What is your best guess for the original number of balls (red plus blue) in the urn?

(FiveThirtyEight)

Solution

In this problem, we are urn detectives. We want to look at the probability that there are $2S$ balls in the urn given that we drew $8$ red balls, and $11$ blue balls, and eyeball the maximum.

Bayesian inference

Using Bayes’ rule, we can write $P(2S\text{ and }{\color{red}8},{\color{blue}{11}})$ two different ways, and find:

The denominator is the same for all values of $S,$ so we can forget about it.

We don’t have any evidence about the number of balls beyond the balls we’ve drawn. So, to ensure we’re unbiased, we use a uniform prior distribution with Dirac spikes at each possible value (starting the sum at $11$ since we drew $11$ blue balls)

By design, this is uniform in $S$ and we can ignore it as well.

This tells us that the likelihood of $2S$ total balls given the observation is proportional to the probability of the observation given that there are $2S$ total balls:

Count ‘em up

The right side can be gotten by counting. There are $\binom{S}{8}\binom{S}{11}$ ways to draw $8$ red balls and $11$ blue balls, and there are $\binom{2S}{19}$ ways to draw any $19$ balls, so:

and our best guess is $\underset{S}{\operatorname{arg max}} P(2S\rvert{\color{red}8},{\color{blue}{11}}).$

Plotting this as a function of $S,$ we see that it’s maximized at $S=17,$ which corresponds to $2S = 34$ total balls in the urn.

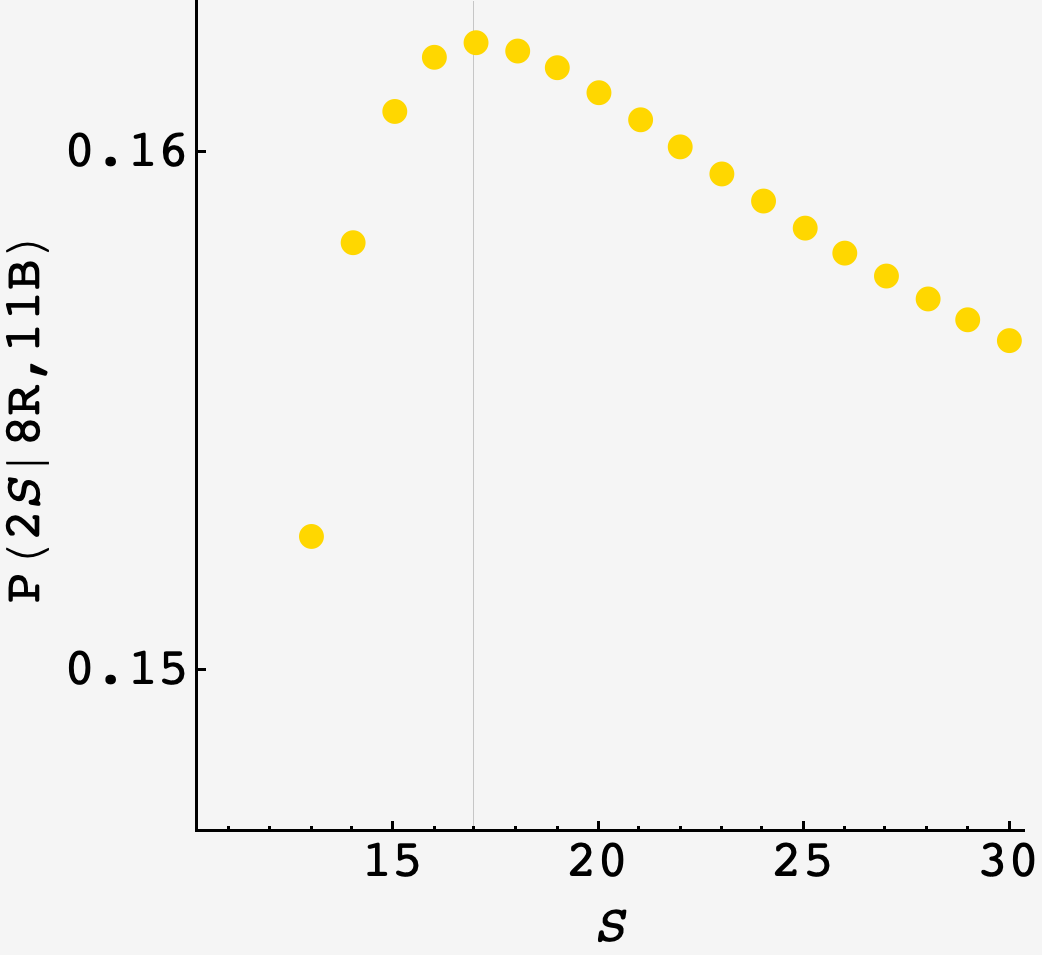
That’s just great.

The letdown

But it’s not that great, because it’s a weak maximum. As $S$ tends to infinity, the curve plateaus about $10\%$ under its maximum value.

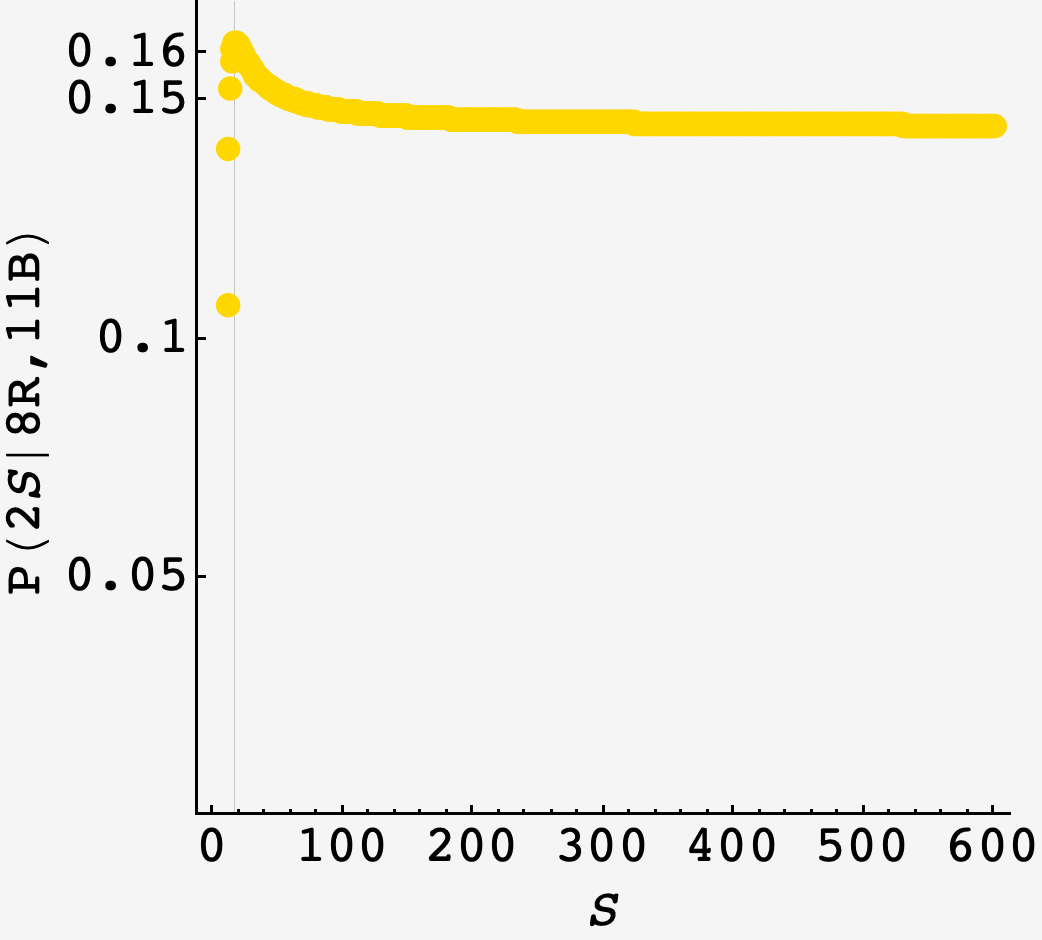
So in the end, it’s anyone’s guess.