Question: The Robot Weightlifting World Championship was such a huge success that the organizers have hired you to help design its sequel: a Robot Tug-of-War Competition!
In each one-on-one matchup, two robots are tied together with a rope. The center of the rope has a marker that begins above position 0 on the ground. The robots then alternate pulling on the rope. The first robot pulls in the positive direction towards 1; the second robot pulls in the negative direction towards $-1.$ Each pull moves the marker a uniformly random draw from $\left[0,1\right]$ towards the pulling robot. If the marker first leaves the interval $\left[-\frac12,\frac12\right]$ past $\frac12,$ the first robot wins. If instead it first leaves the interval past $-\frac12,$ the second robot wins.
However, the organizers quickly noticed that the robot going second is at a disadvantage. They want to handicap the first robot by changing the initial position of the marker on the rope to be at some negative real number. Your job is to compute the position of the marker that makes each matchup a $50:50$ competition between the robots. Find this position to seven significant digits—the integrity of the Robot Tug-of-War Competition hangs in the balance!
Solution
First, let’s get acquainted with the setup:
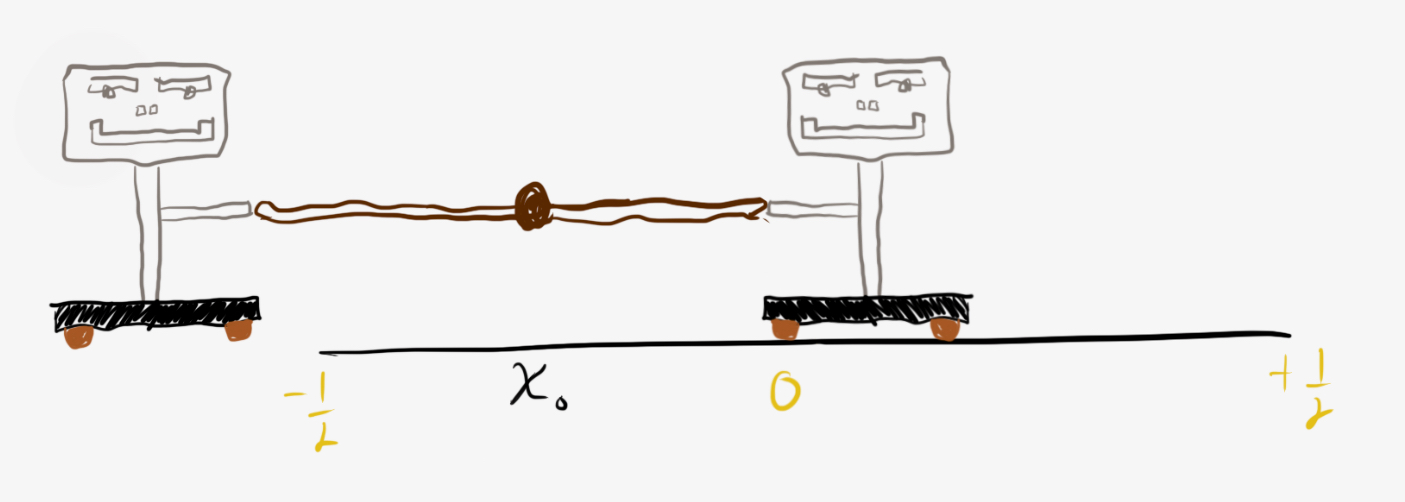
Both robots pull the middle of the rope toward their side a random distance between $0$ and $1.$ If Player 1 gets it past $\frac12,$ then they win (and likewise for Player 2).
Intuition
If it’s Player 1’s turn, they have two ways to win the game:
- they can immediately move the game past $+\frac12,$ or
- they can move it somewhere less than $\frac12,$ and then go on to win
In other words,
\[P_\text{win}({x_0}) = P(\text{win immediately at}\, {x_{0}}) + P(\text{win eventually at}\, {x_{0}}).\]If Player 1 wins immediately, then they have to move beyond $\frac12,$ which has probability $1 - (\frac12 - x_0).$ So,
\[P(\text{win immediately at}\, x_0) = \frac12 + x_0.\]If Player 1 wins eventually, then they have to move the game somewhere to the left of $\frac12,$ then Player 2 has to move it somewhere to the right of $-\frac12,$ and then Player 1 has to win from there.
\[\begin{align} P(\text{win eventually at}\, x_0) &= P(x_0\rightarrow\text{somewhere}\rightarrow\text{somewhere else})\cdot P_\text{win}(\text{somewhere else}) \\ &= P(x_0\rightarrow\text{somewhere})\cdot P(\text{somewhere}\rightarrow\text{somewhere else})\cdot P_\text{win}(\text{somewhere else}) \end{align}\]Path integral
We nearly have an equation for $P_\text{win}(x_0),$ we just have to sum over all the possibilities for $\text{“somewhere”}$ ($x_1$) and $\text{“somewhere else”}$ ($x_2$).
\[P_\text{win}(x_0) = \frac12 + x_0 + \int dx_1 P(x\rightarrow x_1) \int dx_2 P(x_1\rightarrow x_2)P_\text{win}(x_2).\]From the diagram below, $x_1$ can take on any value from $x_0$ up to $\frac12$ without ending the game. Likewise, $x_2$ can take any value from $x_1$ down to $-\frac12.$
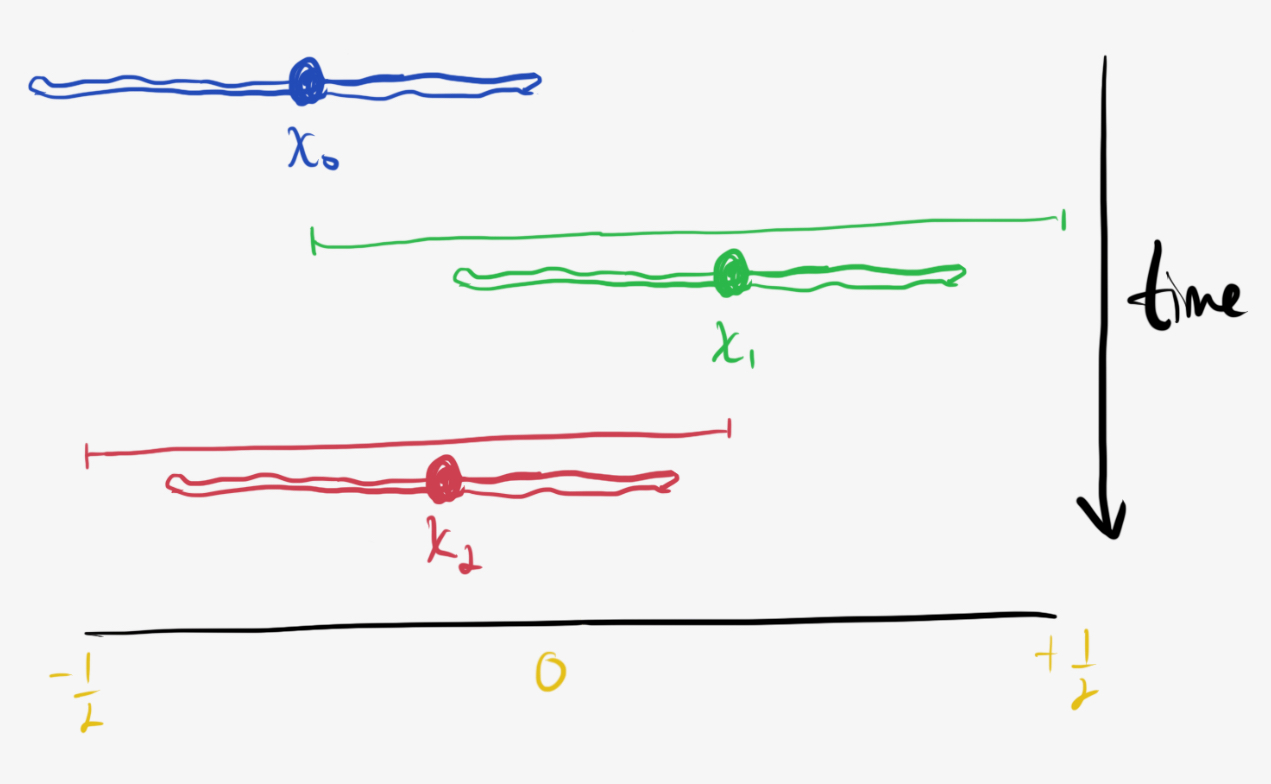
Since $P(x_0\rightarrow x_1)$ and $P(x_1\rightarrow x_2)$ are uniform probabilities on the unit interval, we get:
\[P_\text{win}(x_0) = \frac12 + x_0 + \int\limits_{x_0}^{\frac12} dx_1 \left[\int\limits_{-\frac12}^{x_1} dx_2 P_\text{win}(x_2)\right].\]This is an integral equation for $P_\text{win}(x_0),$ but we can solve it without resorting to transforms.
Finding $P_\text{win}(x)$
Taking the derivative with respect to $x_0,$ we get
\[\partial_{x_0} P_\text{win}(x_0) = 1 - \int\limits_{-\frac12}^{x_0} dx_2 P_\text{win}(x_2).\]Taking another, we get
\[\partial_{x_0}^2 P_\text{win}(x_0) = - P_\text{win}(x_0).\]So, the general form for $P_\text{win}(x_0)$ is, incredibly, the sum of sinusoids
\[P_\text{win}(x_0) = A\sin x_0 + B\cos x_0.\]When the game starts at $x_0=\frac12,$ the chance that Player 1 wins is $1,$ so
\[A\sin\frac12 + B\cos\frac12 = 1.\]We also have the first derivative of the integral equation, that has to be satisfied:
\[\begin{align} A\cos x_0 - B\sin x_0 &= 1 - \left(-A\cos x_0 + B\sin x_0 +A\cos\frac12 + B\sin\frac12\right) \\ &= 1 + A\cos x_0 - B\sin x_0 - A\cos\frac12 - B\sin\frac12 \end{align}\]or $1 = A\cos\frac12 + B\sin\frac12.$
Putting these together, we have $A = B = \left(\sin\frac12 + \cos\frac12\right)^{-1},$ and
\[P_\text{win}(x_0) = \dfrac{\sin x_0 + \cos x_0}{\sin\frac12 + \cos\frac12}.\]Fair beginnings
As written, this is hard to invert, but we can write it more tidily as a single $\cos$ term. Using the complex representation, we get
\[\begin{align} A\sin x + B\cos x &= \Re\left(Ae^{ix} + Be^{i(x - \frac{\pi}{2})}\right) \\ &= \Re\left(e^{ix}\left[A - iB\right]\right) \\ &= \Re(e^{ix}\sqrt{A^2 + B^2}e^{-i\phi}) \\ &= \sqrt{A^2 + B^2}\cos{(x-\phi)} \end{align}\]where $\phi = \cos^{-1}\frac{A}{\sqrt{A^2 + B^2}}.$
When $A=B,$ this gives $\phi = \frac{\pi}{4}$ so
\[P_\text{win}(x_0) = \dfrac{\cos\left(x_0 - \frac{\pi}{4}\right)}{\cos\left(\frac12 - \frac{\pi}{4}\right)}.\]The fair starting point for Player 1 is whatever $x$ makes $P_\text{win}(x) = \frac12$ so
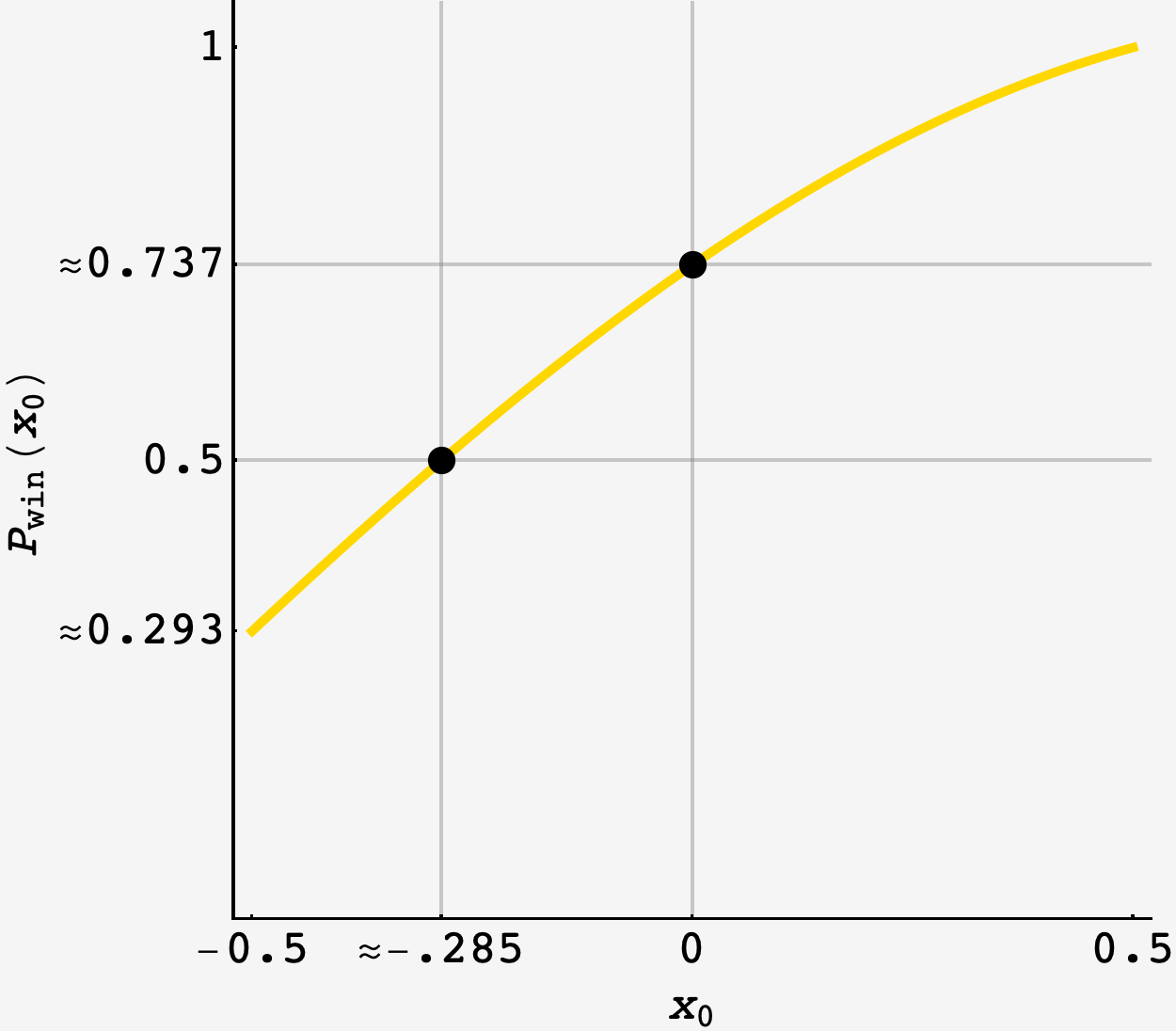
\[\boxed{ \begin{align} x_0 &= \frac{\pi}{4} + \cos^{-1}\left[\frac12 \cos\left(\frac12 - \frac{\pi}{4}\right)\right] \\ &\approx -0.28500012 \end{align} }\]Plotting the win probability we can see that Player 1 wins $\approx 74\%$ of the time if the game starts at the origin. Interestingly, they maintain a $\approx 29\%$ win rate even when we start the game all the way at Player 2’s goal line.