Question: One morning, Phil was playing with his daughter, who loves to cut paper with her safety scissors. She especially likes cutting paper into “strips,” which are rectangular pieces of paper whose shorter sides are at most 1 inch long.
Whenever Phil gives her a piece of standard printer paper (8.5 inches by 11 inches), she picks one of the four sides at random and then cuts a 1-inch wide strip parallel to that side. Next, she discards the strip and repeats the process, picking another side at random and cutting the strip. Eventually, she is left with nothing but strips.
On average, how many cuts will she make before she is left only with strips?
Extra credit: Instead of 8.5 by 11-inch paper, what if the paper measures $m$ by $n$ inches? (And for a special case of this, what if the paper is square?)
Solution
Whenever the daughter cuts a strip from an $m \times n$ sheet of paper, she converts it to an $m \times (n-1)$ or $(m-1) \times n$ sheet of paper, with equal probability. so, the expected number of cuts in the $m \times n$ paper is 1 plus the average number of cuts remaining:
\[\langle c_{m,n}\rangle = 1 + \frac12 \langle c_{m,n-1}\rangle + \frac12 \langle c_{m-1,n}\rangle.\]Because the strip’s short side is equal to $1,$ this has base values of $c_{m,1} = c_{1,m} = 0.$
Generating coefficients
At this point we could get the expected length by recursion, but it isn’t too hard to get analytically.
If we multiply through by $x^m y^n$ and sum over all values of $m$ and $n,$ we get the generating function
\[C(x,y) = \sum\limits_{m=2}^{\infty} \sum\limits_{n=2}^{\infty} x^my^n \langle c_{m,n}\rangle.\]By design, the coefficient of the, e.g., $x^my^n$ term in this series is equal to expect number of cuts for the $m\times n$ piece of paper. Carrying out this sum for both sides:
\[\begin{align} C(x,y) &= \sum\limits_{m=2}^{\infty}\sum\limits_{n=2}^{\infty} \left[x^my^n + x^my^n \langle c_{m,n-1}\rangle + x^my^n \langle c_{m-1,n}\rangle\right] \\ &= \frac{x^2y^2}{\left(1-x\right)\left(1-y\right)} + \frac12 xC(x,y) + \frac12 yC(x,y), \end{align}\]or
\[C(x,y) = \dfrac{x^2y^2}{\left(1-x\right)\left(1-y\right)} \cdot \dfrac{1}{1-\dfrac{x+y}{2}}\]To find the expected number of cuts for an $m\times n$ sheet of paper, we need the coefficient of the $x^my^n$ term in $C(x,y).$
Writing out the first few terms in each piece, we get
\[\begin{align} C(x,y) = x^2y^2&\left(1+x+y+xy+x^2y+xy^2+\ldots\right)\cdot\\ &\left[1 + \frac{x+y}{2} + \left(\frac{x+y}{2}\right)^2 + \left(\frac{x+y}{2}\right)^3 + \ldots\right] \end{align}\]What are the contributions to the $x^my^n$ term?
The first series contains one copy of every term $x^my^n,$ so, it is able to promote every term in the second series, from $x^0y^0$ up to $x^{m-2}y^{n-2},$ into a $x^my^n$ term.
The coefficients of the terms in the second series are the binomial coefficients divided by a power of $2,$ so the $x^my^n$ coefficient of $C(x,y)$ is simply
\[\boxed{ \langle c_{m,n}\rangle = \sum\limits_{m^\prime=0}^{m-2}\sum\limits_{n^\prime=0}^{n-2}\dfrac{\binom{n^\prime+m^\prime}{m^\prime}}{2^{m^\prime+n^\prime}} }.\]Plugging in the values for the $8.5\text{ in}\times 11\text{ in}$ piece of paper, we get
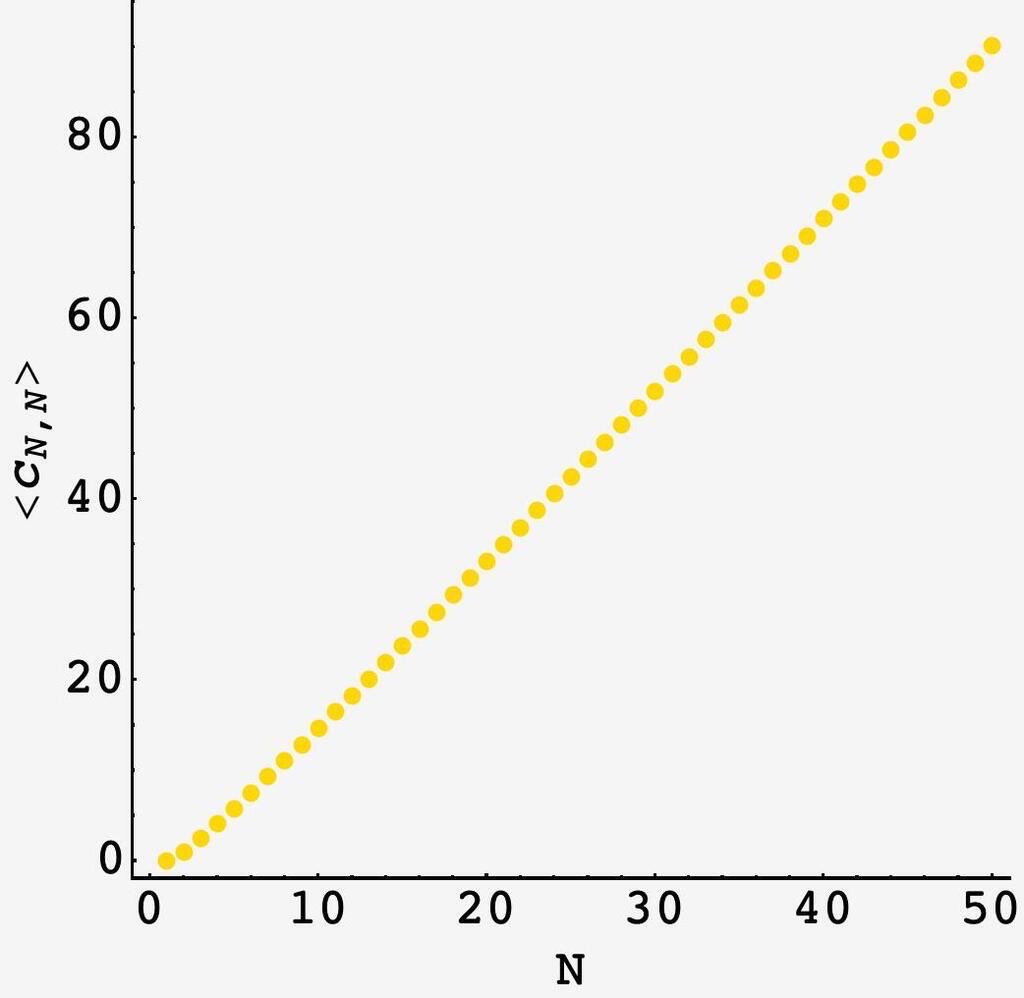
\[\langle c_{9,11}\rangle = \frac{234137}{16384} \approx 14.29059\]With the analytic form in hand, we can explore the behavior in two cases. First, $m=n$ in square sheets of paper, and $\langle C_{m,m}\rangle$ is approximately linear from $m=2$ on:
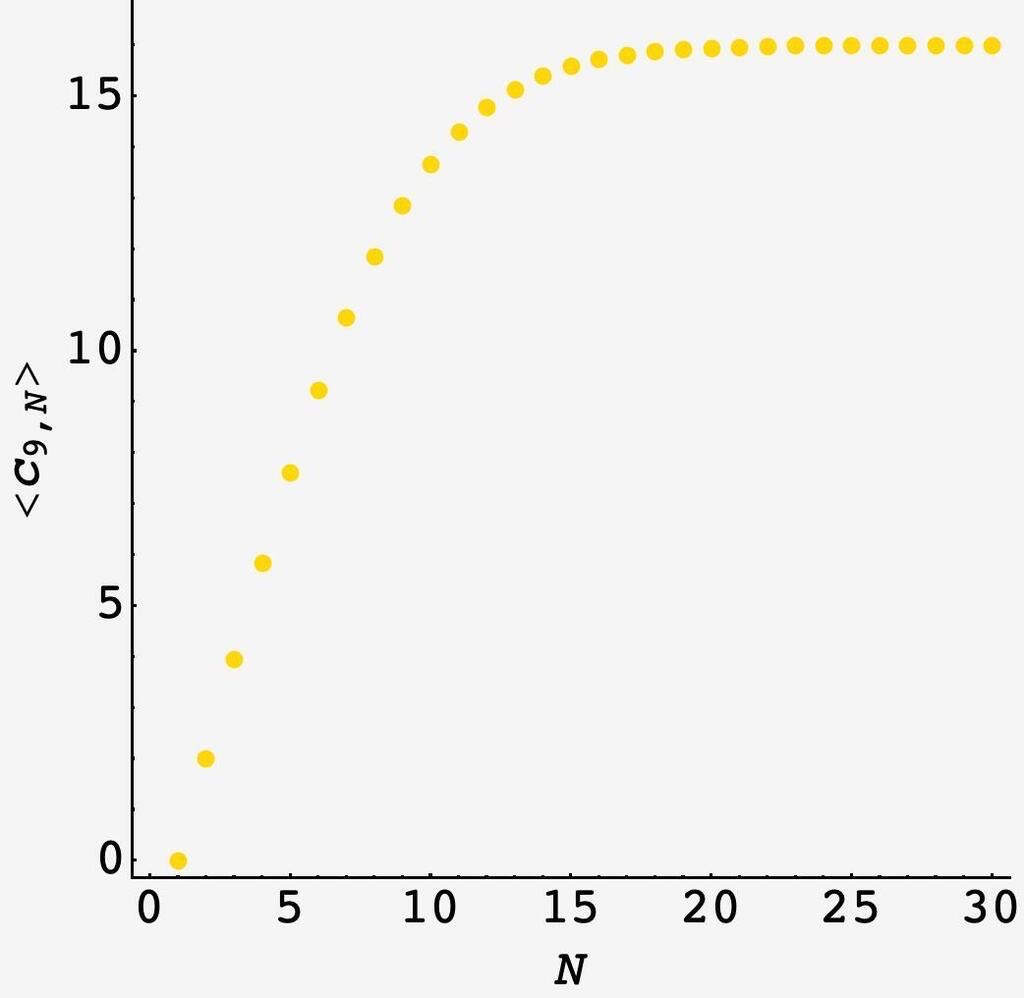
If on the other hand, we have a rectangular sheet of paper, $\langle c\rangle$ grows approximately linearly until the paper is square, after which the expected number of cuts is harshly thresholded:
As $n$ grows large, the sum over $n$ becomes $2,$ regardless of $m,$ while the sum over $m$ gets us a factor of $(m-1)$ and, so, we get $\lim\limits_{n\rightarrow\infty} \langle c_{m,n}\rangle = 2(m-1).$