Question: Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of $15$ miles per hour — to the other end zone, $100$ yards away.
At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, $50$ yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.
Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
Solution
First, we can work in the reference frame of the chaser to find the speed of the closing of the gap.
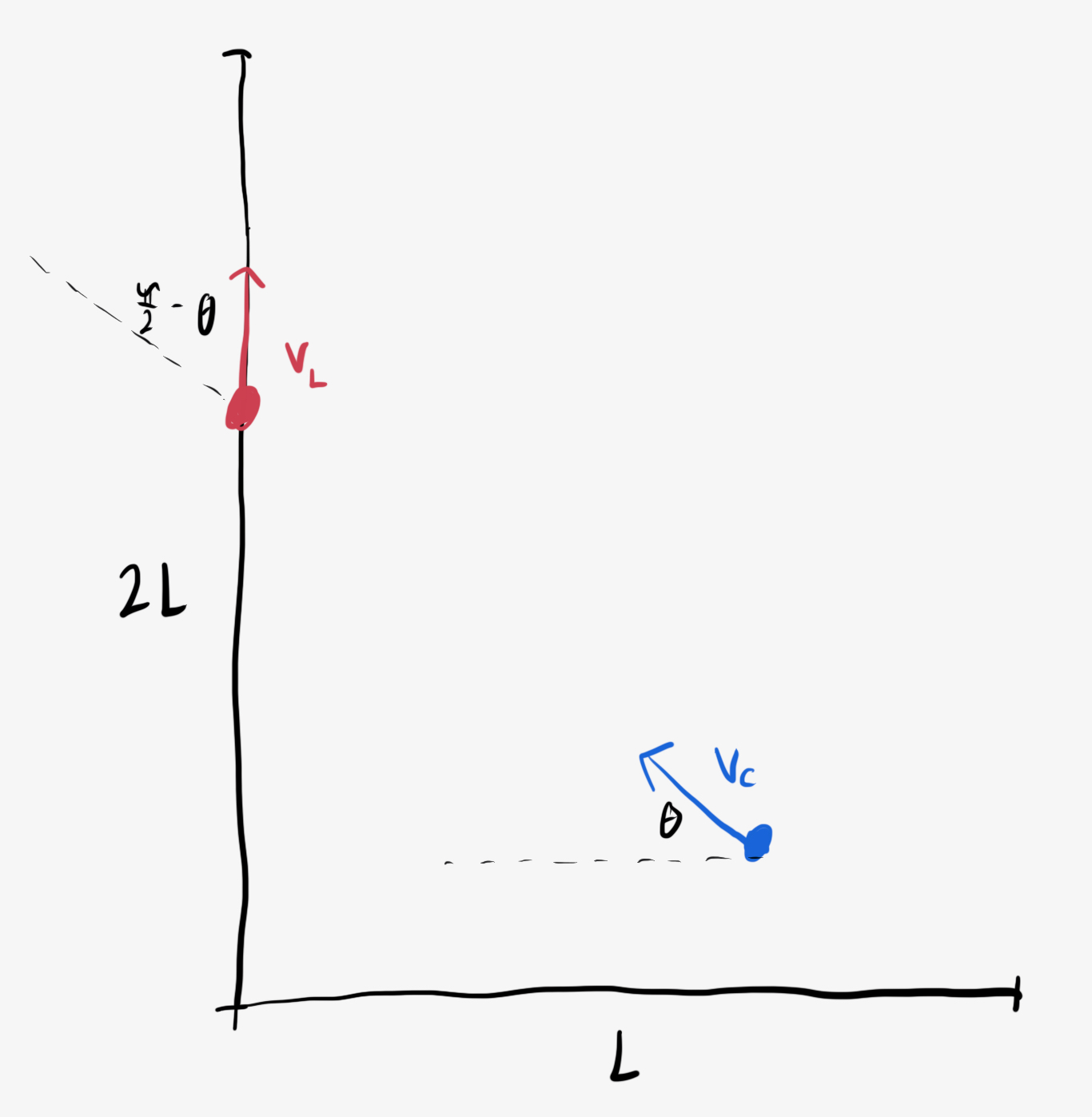
The chaser moves directly at the leader so their motion only works to close the gap. But the leader moves away from the chaser, so long as their trajectories are not parallel. If the chaser makes an angle $\theta$ with the $x$-axis, then the leader’s velocity in the frame of the chaser is $V_L \langle \cos(\frac{\pi}{2} - \theta(t)),\ \sin(\frac{\pi}{2} - \theta(t))\rangle = V_L\langle \sin\theta(t),\ \cos\theta(t)\rangle.$
So, the chaser closes the gap with speed $V_\text{rel} = V_L\sin\theta(t) - V_C.$
Over the course of the chase, this gap shrinks by $L,$ so
\[\begin{align} -L &= \int\limits_0^T dt \left(V_L\sin\theta(t) - V_C\right) \\ &= V_L\left(\int\limits_0^T dt\, \sin\theta(t)\right) - V_C T. \end{align}\]In principle, this integral requires us to know the behavior of $\theta(t).$ In practice, the same integral pops up in a simpler problem: the total distance that the chaser moves upfield, $2L.$
In the coordinate system of the field, their velocity is $V_C\langle \cos\theta(t),\ \sin\theta(t)\rangle,$ so their total displacement upfield is just
\[2L = V_C\left(\int\limits_0^T dt\, \sin\theta(t)\right).\]Since we’re looking for the minimal value of $V_C$ that allows them to catch up before the goal line, $T = 2L/V_L,$ the time when the leader gets to the endzone.
This leaves us with an algebra problem for $V_C$. Calling the integral $S,$ we get:
\[\begin{align} -L &= V_L S - 2L\frac{V_C}{V_L} \\ 2L &= V_C S \end{align}\]or
\[\begin{align} -L &= 2L\frac{V_L}{V_C} - 2L\frac{V_C}{V_L} \\ 1 &= 2\frac{V_C^2 - V_L^2}{V_LV_C} \end{align}\]which we can solve to find $V_C$ in terms of $V_L$:
\[\begin{align} V_C &= \dfrac{1+\sqrt{17}}{4}\times V_L \\ &\approx 1.280776\times V_L \\ &\approx 19.21164\,\text{mph} \end{align}\]