Uniform Dice

Question: When you roll a pair of fair dice, the most likely outcome is $7$ (which occurs $1/6^\text{th}$ of the time) and the least likely outcomes are 2 and 12 (which each occur $1/36^\text{th}$ of the time).

Annoyed by the variance of these probabilities, I set out to create a pair of “uniform dice.” These dice still have sides that are uniquely numbered from $1$ to $6,$ and they are identical to each other. However, they are weighted so that their sum is more uniformly distributed between $2$ and $12$ than that of fair dice.

Unfortunately, it is impossible to create a pair of such dice so that the probabilities of all $11$ sums from $2$ to $12$ are identical (i.e., they are all $1/11$). But I bet we can get pretty close.

The variance of the $11$ probabilities is the average value of the squared difference between each probability and the average probability (which is, again, $1/11$). One way to make my dice as uniform as possible is to minimize this variance.

So how should I make my dice as uniform as possible? In other words, which specific weighting of the dice minimizes the variance among the $11$ probabilities? That is, what should the probabilities be for rolling $1, 2, 3, 4, 5$ or $6$ with one of the dice?

(FiveThirtyEight)

Solution

The unusual goal before us is to make the odds of each sum as uniform as we can. We want the odds to roll $1+1=2$ as close to the odds of $1+6=2+5=3+4=7$ as possible.

So we are interested in the variance of the probability of a pair of dice appearing which, as a subtask, entails finding the expectation value of the probability of a pair of dice appearing!

The second part is easy. Since $\sum_i p_i = 1,$ and there are $11$ possible outcomes for two dice, we get $\langle p\rangle = \frac{1}{11}.$

Add it up

The first part is a little spicy.

We are looking at the sum

They start out simple — consider the $\left(1,1\right)$ outcome, which has probability $p_1^2.$ But by the $6$, which can come out one of five ways

we have a mess on our hands.

Slim it down

Adding it up, this generates a big polynomial that we have to minimize.

On its face this has six variables, $\{p_i\}_{i=1}^6,$ but, happily, a moment’s thought can reduce it to three.

The variables describing sides $1, 2,$ and $3$ are symmetric with the variables describing sides $4, 5,$ and $6,$ respectively, so we can replace $p_4\rightarrow p_1, p_5\rightarrow p_2,$ and $p_6\rightarrow p_3.$

Putting it all together, we have the code below

ps = {p1, p2, p3, p4, p5, p6};

Z =
 Sum[
   ps[[i]] ps[[j]] z^(i + j)
   , {i, 1, 6}
   , {j, 1, 6}
   ] /. {p6 -> p1, p5 -> p2, p4 -> p3}

coefficients = CoefficientList[Z, z][[3 ;; -1]]

mean = 1/11
variance =
 1/11 Sum[(coefficients[[i]] - mean)^2, {i, 1, Length@coefficients}]

solution = NMinimize[
  {variance,
   { 0 <= p1 <= 1/2
   , 0 <= p2 <= 1/2
   , 0 <= p3 <= 1/2
   , p1 + p2 + p3 == 1/2
   }
  }
  , {p1, p2, p3}
 ]

which shows that the minimum variance is $\sigma^2_\text{min}\approx 0.00121758$ which is realized by assigning $p_1=p_6=0.243883,$ $p_2=p_5\approx 0.137479,$ and $p_3=p_4\approx 0.118638.$

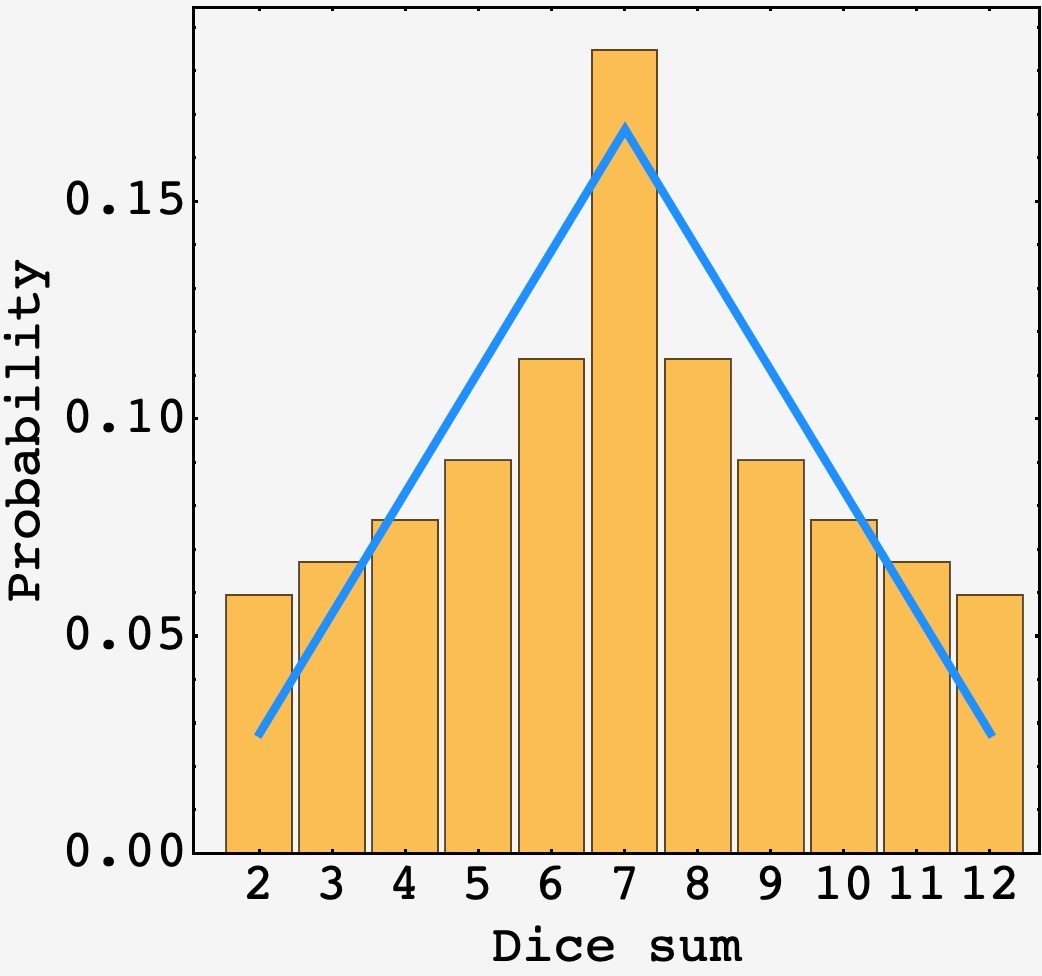
This produces the following distribution for the dice sum probabilities:

The yellow bars show the minimal variance distribution, and the blue curve shows the distribution for regulation die.

As expected, the distribution is symmetric about $7.$

For posterity, the approximate numerical values are: