Crescent Observatory

Question: you’re watching the Moon from your room, alone, like every night. Seeking a higher purpose, you decide to track the projected area of the illuminated portion of the Moon throughout the month. If your data is accurate, how much faster will the illuminated Moon’s area be growing at half Moon as compared to a crescent Moon of $1/6^\text{th}$ area?

(FiveThirtyEight)

Solution

Some moonlight basics

• The reason we don’t see the Moon during the day because it’s on the other side of the Earth. The Moon takes $\sim 30$ days to orbit Earth, so we are effectively sampling it once a day throughout its orbit.

• The reason we see the Moon at night is that it’s illuminated by the Sun. Since the Moon’s orbital plane isn’t the the plane of Earth’s orbit around the Sun, sunlight fully illuminates one side of the Moon.

• The reason that Moon’s shape seems to change throughout the month is that its illuminated half changes the angle it makes with Earth. When Moon, Earth, and Sun we perfectly lined up (in that order), we see a full Moon. Similarly, when the Moon is in front of Earth, we see a nearly black (New) Moon.

• Finally, since the Moon’s orbit takes a fixed amount of time, the angle that the Moon-Sun line makes with Earth varies uniformly throughout the month.

Patchwork Moon

If we want to measure the illuminated area of the Moon, we can divide the Moon up into patches, and count which ones are lit up.

First, let’s worry about the surface area of the patch, i.e., the area it would present to us if we looked at it flat.

We can introduce some coordinates to measure along the surface.

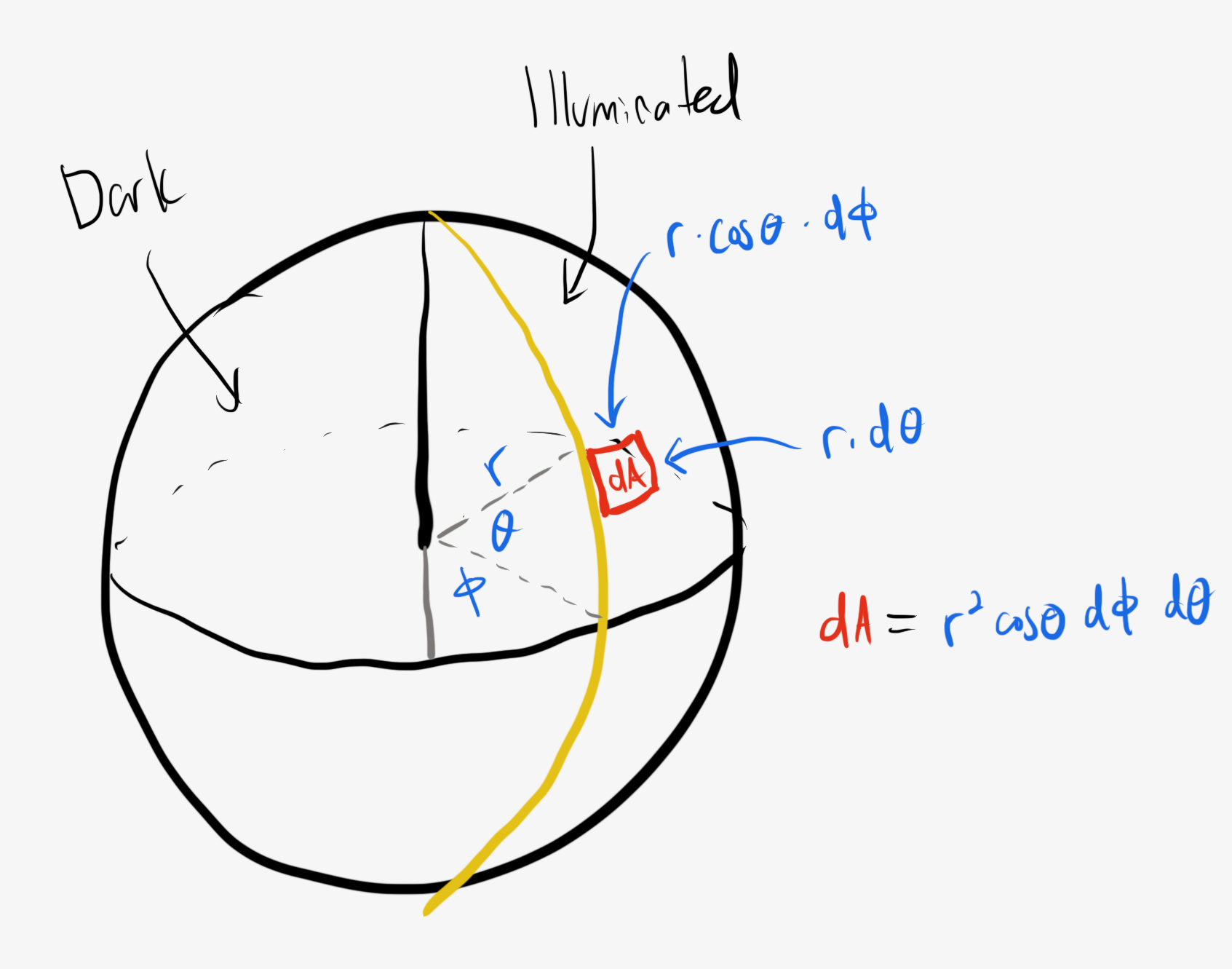
First of all, the patch is located at some angle $\phi$ away from the direct line of sight from Earth to the center of the Moon. Additionally, it is located at another angle $\theta$ above the equator established by the line of sight from Earth. The patch itself has some angular extent $d\phi$ and $d\theta.$ Even though the Moon is curved, since these angles are small, the patch is effectively a rectangle, and its area is just $r\,d\theta$ by $r\cos\theta\,d\phi,$ or $dA = r^2\cos\theta\,d\theta\,d\phi.$

Tilting at patches

Now, we don’t see the patches straight on from where we are on Earth. Instead, we see them tilted by the angles $\theta$ and $\phi.$ As we’ll see below, this affects the projected $2\text{D}$ area we see from Earth in a simple way.

To get some intuition, take a book and stand it up perpendicular to the ground. This is the area $dA:$

Now, tilt the book backward so that it makes some angle $\theta$ with the ground. This will preserve the width of the book while shortening the height to $\sin\theta$ times its original height. (Note: because my book is $\sim 3$ feet away instead of hundreds of thousands of miles, perspective gives the illusion of a trapezoid, but the patch remains rectangular — for an infinitesimal patch, $r$ doesn’t vary in these projections.)

Now, rotate the book an angle $\phi$ from its current orientation, which will further slim the book’s profile. Its original width goes from $w$ to $w\cos\phi,$ bringing the area of the path from $dA$ to $dA\sin\theta\cos\phi.$

The definition of $\theta$ in the Moon system and for the book are different and, when we account for the change, $\sin\theta$ becomes $\cos\theta,$ bringing the new patch area to $dA^\prime = dA\cos\theta\cos\phi = d\phi\,d\theta\,r^2\cos^2\phi\cos\theta.$

Sewing the patches

Now, the illuminated region spans from $\theta = -\pi/2$ to $\theta = +\pi/2$ and from whatever angle $\phi_\text{min}$ to $\phi=+\pi/2,$ with $\phi_\text{min}$ depending on the phase the Moon is in. To get the illuminated projected area, we just need to add up the area of all the little patches to the right of the yellow line:

It is a good sign that when $\phi_\text{min} = -\pi/2,$ this expression gives $\pi r^2,$ the area of a circle, the flat projection of the Moon.

Moon vs Moon

The problem asks us to compare the situations at $1/6$ and $1/2$ illumination. To make the analysis simpler, let’s divide the area of the illuminated region by $\pi r^2$ to get the function $f(\phi_\text{min}) = \dfrac{1 - \sin \phi_\text{min}}{2}.$ Obviously, $f(0) = 1/2,$ but for what $\phi_\text{min}$ does $f$ equal $1/6$?

and $\phi_\text{min} = \arcsin \frac23.$

Now, the relative rate of increase of the illuminated area is just $f^\prime(\phi_\text{min}) = \frac12 \cos\phi_\text{min}$ (because of our definition for $\phi,$ it decreases as the area increases, which flips the sign).

So, the relative rate of increase is