Random Reverse Jenga

Question: relaxing at home for the $55^\text{th}$ week running, you have an idea to play reverse Jenga, stacking blocks one at a time to see how high you can get them before some blocks fall down. To make it a surprise, you place each new blocks center randomly at some place between the edges of the block underneath. About how many blocks do you expect to place before seeing a unit of blocks tumble down?

(FiveThirtyEight)

Solution

The basic concept here is that when the center of mass of an “object” is between the edges of the surface it rests on, then it won’t topple. If this is true at every level of the tower, then the whole tower will be stable. “object” is in square quote because at each level, an object is whatever collection of blocks currently sits above that level, in whatever configuration they currently sit in.

With each new block that’s added, there is the potential for a center of mass to move outside the bounds of the surface it rests upon. So, we have to keep track of the balance at each level (after the first block).

Observations

The first block can’t tip over, and the second block can’t tip unless it has something on top of it. Therefore, the smallest number of blocks we expect to accumulate before a collapse is $3$.

Because each block can be at most $\Delta b=1/2$ from the middle of the one underneath it, both Block $2$ and Block $3$ need to be placed in the same “direction” relative to the middle of the first block. For them to tip, it has to be true that

This is the area under the line $\Delta b_3 = 1 - \Delta b_2,$ which is

The center of mass of a collection of identical blocks is the average position of their centers of mass. Since the offsets $\Delta b_i$ measure the gap between the center of masses of consecutive blocks, the position of a block relative to another block is equal to the sum of the offsets for all the blocks between them. i.e. the distance between Block $2$ and Block $6$ is ${\left(\Delta b_3 + \Delta b_4 + \Delta b_5 + \Delta b_6\right)}.$

By extension, the center of mass of the Block $3$-through-Block $6$ system relative to the edge of Block $2$ is (after gathering terms)

This is a core sum, so we capture it in the function running_mean() in the code.

With that in place, the big picture is to go through the tower, adding one block at a time, checking whether each “system’s” center of mass overhangs the edge of the block it sits upon. Running this code for $10^7$ rounds gets an estimate of $\langle B\rangle \approx 7.1106446$ blocks before a topple occurs.

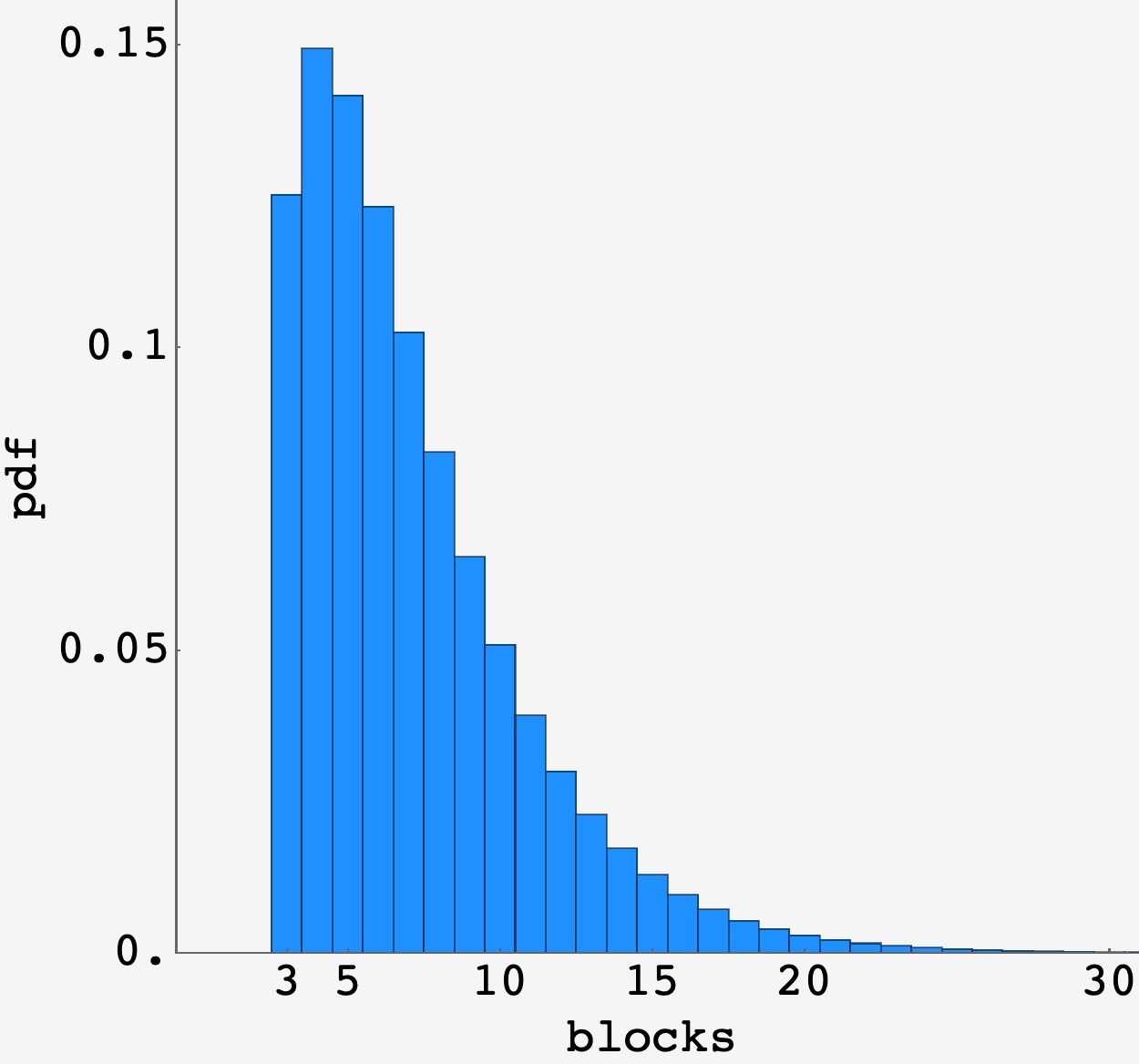
Empirical distribution of tower heights upon first topple.

As expected, topples of $3$-block towers account for $1/8^\text{th}$ of all topples.

def running_mean(lst):
    L = len(lst)
    return sum((L-i)*lst[i] for i in range(L)) / L

def new_offset():
  return random.uniform(-1/2, +1/2)

def round():
    offsets = [new_offset()]
    (blocks, topple) = (2, False)
    
    while not topple:
        offsets.append(new_offset())
        means = [running_mean(offsets[_:]) for _ in range(len(offsets))]
        blocks += 1
        if any(abs(_) > 0.5 for _ in means):
            topple = True
            
    return blocks