Gaussian Skiers

Question: You’re in your town’s heat to head marble racing championship, the traditional way to determine who is the town’s next mayor. The race is split into two heats and your time in either heat is a random, normally distributed variable. If you have the fastest time in the first run, what is the probability $P_\text{win it all}$ that you end up winning the event, as determined by the sum of your times on heat run? Extra credit: what if there are $29$ other candidates in the race?

(FiveThirtyEight)

Solution

If the first skier wins the first round by $\Delta T_1,$ they will prevail so long as they don’t lose the second round by more than $\Delta T_1.$

The gap between the first round times $\left(\Delta T_1 = t^\text{A}_1 - t^\text{B}_1\right)$ which has some symmetric distribution $P(\Delta T_1).$ Since we know that person $\text{A}$ won the first round, we condition on the left side of $P$ and the expected value of $\Delta T_1$ is whatever the $25^\text{th}$ percentile of the distribution is.

If person $\text{A}$ is to win overall, $\Delta T_1$ has to be less than or equal to $-\Delta T_2.$ The gap in the second round is a random variable from the same distribution, so the chance that $\Delta T_1 < -\Delta T_2$ (and, therefore, that player $\text{A}$ wins) is $P_2 = 1 - 0.25 = 0.75.$

Pushing on

There are several ways to manifest the result above through calculation but none of the them yielded to generalization. An approximate attempt yielded good results for low $N$ but broke down as $N$ grew, notably resisting the stable plateauing that persists near $30\%$ for a wide range of $N.$

A simulation suggests a roughly linear decrease on log-log axes, and yields $P_{30} \approx 0.314409.$ Its overall behavior is decently approximated by $P \approx x^{-1/3}$ over a wide range:

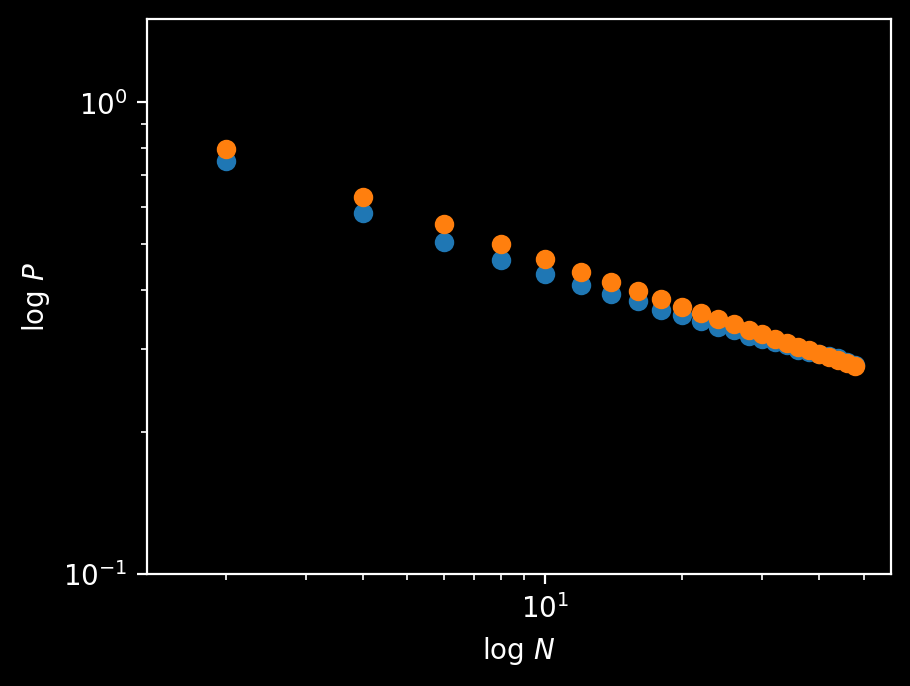
Fig: plot of $\log P(\text{first round winner wins})$ vs $\log N.$

def round(N):
    data = [np.random.normal() for _ in range(N)]
    first_win = data.index(min(data))
    for i in range(N):
        data[i] += np.random.normal()
    overall_win = data.index(min(data))
    if first_win == overall_win:
        return 1
    else:
        return 0
  
domain = range(2, 50, 2)
datapoints = [np.mean([round(N) for _ in range(100000)])  for N in domain]

My attempts at an approximate solution for $N=30$ got the right shape, but took too long to “turn up”. Updates forthcoming if I make progress.