Question: The Fiddler Basketball Association’s All-Star Game consists of two teams: “East” and “West.” Every year these two teams play a game, each with a $50$ percent chance of winning that’s independent of the outcomes of previous years.
Many, many years into the future, you look at the most recent results of the All-Star Game. On average, what is the longest current winning streak that one of the teams is on? (Here, having won only the most recent game still counts as a “streak” of one game.)
Extra credit
To spice up the All-Star Game, the commissioner of the FBA has decided that there will now be three teams competing in All-Star Games: “Stars,” “Stripes,” and “International.” Each year, two of the three teams play each other. If one year has Stars vs. Stripes, the next year has Stripes vs. International, the year after that has International vs. Stars, and then the cycle repeats with Stars vs. Stripes.
Many, many years after this new format has been adopted, you look at the most recent results of the All-Star game. On average, what is the longest current winning streak that one of the teams is on? (As before, having won one game counts as a “streak.” Also, note that the team with the longest winning streak might not be one of the two teams that played in the most recent All-Star Game.)
Solution
The two player game is a special case of the three player game, so we’ll do three first.
Three player game
Since we’re deep in the game, the current game has no dependence on the initial conditions.
If the maximum active streak is $2$ or more, then the leader is unique. That’s because the only win the other two players can have is from playing each other, before immediately losing to the leader. So, when the leader is steamrolling, the other two can’t “catch up” and we can focus on the leader extending their own streak.
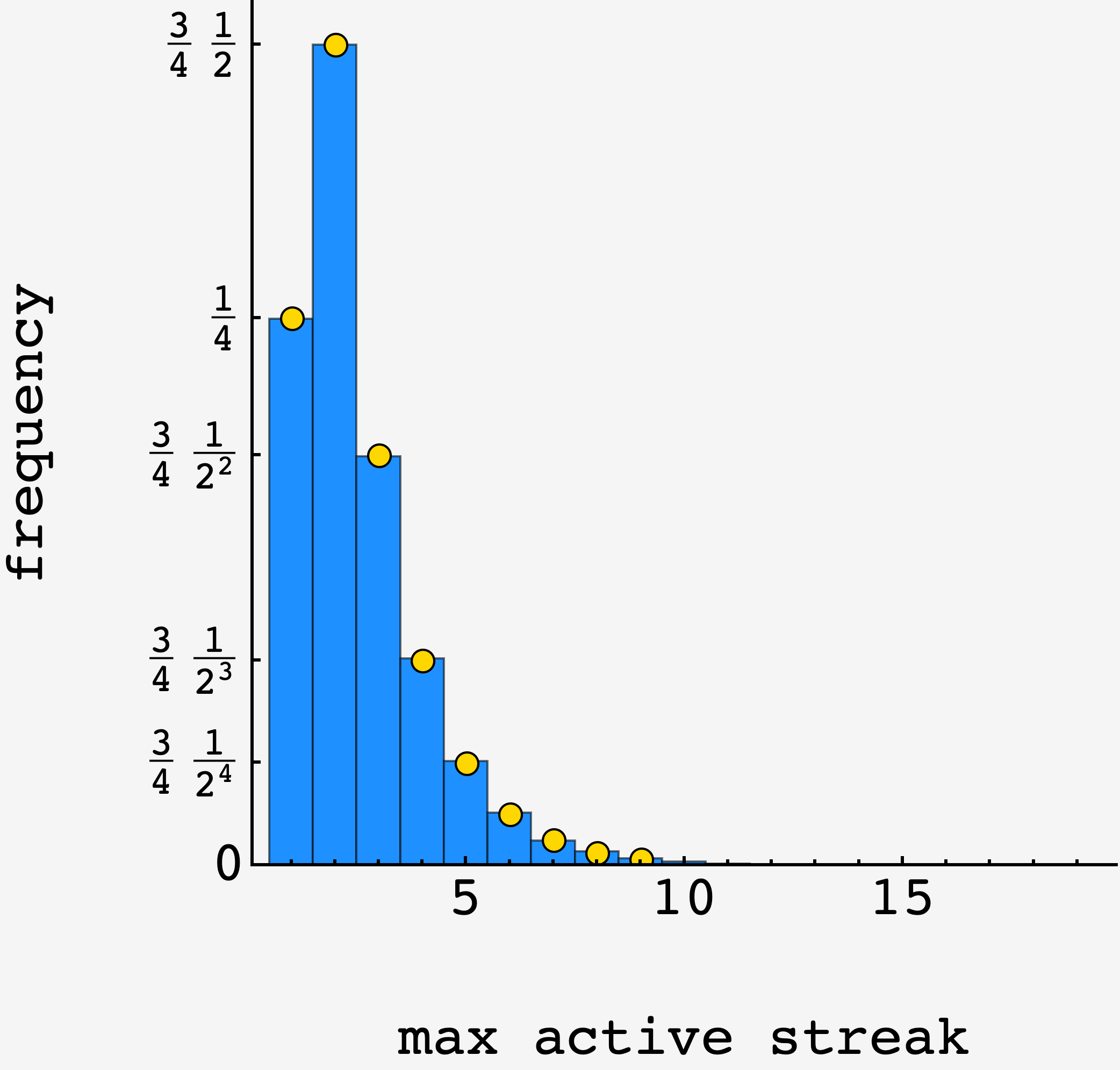
For the leader to have a streak of $2$ or more, they need to have won their last two games. Any of the three players can be the leader, so ${P(S\gt 1) = 3\cdot\frac12\cdot\frac12 = \frac34.}$ Likewise, the chance that the maximum active streak is $1$ is ${\left(1-\frac34\right) = \frac14.}$
The expected number of additional wins for the leader (beyond $2$) is
\[\begin{align} W &= \frac12\cdot 0 + \frac12\cdot(1 + W) \\ &= 1. \end{align}\]So, the expected maximum active streak is
\[\begin{align} \langle S\rangle &= \frac14\cdot 1 + \frac34\cdot(2+1) \\ &= \frac52. \end{align}\]This closely matches a $N=100,000$ trial simulation which got $2.49729.$
trial3[] := (
{s1, s2, s3} = {0, 0, 0};
Do[
If[Mod[j, 3] == 1,
If[RandomReal[] > 1/2, s1 += 1; s2 = 0, s1 = 0; s2 += 1];
];
If[Mod[j, 3] == 2,
If[RandomReal[] > 1/2, s2 += 1; s3 = 0, s2 = 0; s3 += 1];
];
If[Mod[j, 3] == 0,
If[RandomReal[] > 1/2, s3 += 1; s1 = 0, s3 = 0; s1 += 1];
];
, {j, 1, 5000}
];
Return[{s1, s2, s3}]
)
answer = Mean@ParallelTable[Max@trial3[], {j, 1, 100000}]
From the calculation above, we can extract the distribution which is $1/4$ for $S=1$ and $3/4\times 1/2^{S-1}$ for $S\geq 2$ (prediction in gold, simulation in blue)
Two player game
The current leader has at least $1$ game won and they’re expected to win $1$ more, so ${\langle S \rangle = 1 + 1 = 2.}$