Question: It’s coming to the end of the year, which can only mean one thing: time for this year’s Robot Javelin finals! Whoa wait, you’ve never heard of Robot Javelin? Well then! Allow me to explain the rules:
It’s head-to-head. Each of two robots makes their first throw, whose distance is a real number drawn uniformly from $[0, 1].$ Then, without knowledge of their competitor’s result, each robot decides whether to keep their current distance or erase it and go for a second throw, whose distance they must keep (it is also drawn uniformly from $[0, 1]$). The robot with the larger final distance wins.
This year’s finals pits your robot, Java-lin, against the challenger, Spears Robot. Now, robots have been competing honorably for years and have settled into the Nash equilibrium for this game. However, you have just learned that Spears Robot has found and exploited a leak in the protocol of the game. They can receive a single bit of information telling them whether their opponent’s first throw (distance) was above or below some threshold $d$ of their choosing before deciding whether to go for a second throw. Spears has presumably chosen $d$ to maximize their chance of winning — no wonder they made it to the finals!
Spears Robot isn’t aware that you’ve learned this fact; they are assuming Java-lin is using the Nash equilibrium. If you were to adjust Java-lin’s strategy to maximize its odds of winning given this, what would be Java-lin’s updated probability of winning? Please give the answer in exact terms, or as a decimal rounded to $10$ places.
Solution
Before we embark on calculating, let’s sketch the big picture of $S$ and $J$’s strategies:
- in the first level of belief, the two players want to find the value of the first roll where their expected score is the same whether they reroll or stay put. This is their unperturbed Nash equilibrium.
- at the second level, $S$ is able to learn if $J$’s first roll exceeds a threshold and, as a result, $S$ should be able to be less aggressive when $J$’s first is low, and more aggressive when $J$’s first roll is high.
- at the third level of belief, $J$ knows exactly what thresholds $S$ is using to trigger their rerolls and so, in turn, can modify their threshold for reroll. Since $S$ is less aggressive when $J_1$ is under $d,$ and more aggressive above, $J$ can move their threshold under $d.$
Given the three thresholds we gather from that analysis ($J$’s new threshold $h$, and $S$’s low and high thresholds, $t_-$ and $t_+$), we can add up the probabilities of all scenarios where $J$ is victorious to find $P(J\,\text{wins}).$
Level 1: the unperturbed game
In the unperturbed, symmetric game, $S$ and $J$ only know their own first roll plus the fact that the other player is in the same situation. This means that their strategy has to be something of the form “if my first roll is greater than $t$, then keep it, else reroll.” The value of that threshold will be set at the point where their expected probability of winning is the same whether they reroll or stay put. Intuitively, below this point they will be playing too conservatively, and above this point too aggressively.
Let’s analyze the position of one of the players, $J,$ whose first roll we suppose is exactly at the threshold $c.$ The probability that they win without rerolling is the probability that $S_1$ is below the threshold ($c$) and goes on to reroll $S_2$ below the threshold ($c$ again), so the total probability is $c\times c=c^2.$
In the case where $J$ rerolls, they have two ways to win. One is if $S$ stays put because $S_1$ is over the threshold and lose to $J$’s reroll $J_2 > S_1,$ and the second is if $S$ rerolls and loses to $J$’s reroll $J_2 > S_2.$. The first has probability $(1-c)$ and the second has probability $c\times\tfrac12$ for a total of $1 - \tfrac12c.$
Setting these equal, we get
\[\begin{align} (1-c) + \frac12 c &= c^2\\ 0 &= c^2 +\frac12c - 1 \end{align}\]which has physical root
\[\begin{align} c &= \tfrac12\left(\sqrt{5} - 1\right) \\ &\approx 0.61803399\ldots \end{align}\]Level 2: the perturbed game
In the second level of the game, $S$ understands $J$ to be playing the standard game while $S$ has secret information from their fuzzy surveillance bit. They will find out if $J$’s first roll exceeds their chosen threshold $d.$ This allows $S$ to set their threshold to $t_+$ or $t_-$ based on the value of the bit.
Before we calculate, we can anticipate some aspects of the thresholds. First of all, $d$ should be at least $c$ since $S$ believes $J$ will reroll for anything less than $c.$ Second, since $d \geq c,$ $t_+$ should be greater than $c$ since we know $J_1$ is on average $\tfrac12(1 + c).$ Finally, if we can be sure that $J$ is rerolling, the ideal threshold to use is $t_- = \tfrac12$ since a reroll is expected to be $\tfrac12.$
First, the scenario where $S$ learns that $J_1 \leq d.$ This has four scenarios where $S$ ends up winning:
- $S$ keeps their first roll, $J$ rerolls and still loses. This means $S_1 > t_-,$ $J_1 < c,$ and $J_2 < S_1.$
- $S$ and $J$ both reroll, and $S$ wins. This means $S_1 < t_-,$ $J_1 < c,$ and $J_2 < S_2.$
- $S$ and $J$ keep their first roll and $S$ wins. This means $\max{c,t_-} < S_1 < 1$ and $c < J_1 < \min{S_1, d}.$
- $S$ rerolls and $J$ doesn’t, and $S$ wins. This means $S_1 < t_-$ and $c < J_1 < \min{S_1,d}.$
Put to integrals, these become
\[\begin{align} P(J\,\text{wins}, J_1 < d) &= c\int\limits_{t_-}^1\text{d}S_1 \int\limits_{0}^{S_1}\text{d}J_1 \\ &\quad + ct_- \int\limits_{0}^1\text{d}S_2 \int\limits_{0}^{S_2}\text{d}J_2 \\ &\quad + \int\limits_{\max\{c,t_-\}}^1\text{d}S_1 \int\limits_{c}^{\min\{S_1,d\}}\text{d}J_1 \\ &\quad + t_- \int\limits_{c}^1\text{d}S_1 \int\limits_{c}^{\min\{S_1,d\}}\text{d}J_2 \\ &= \frac12\left(c^2(1+t_-) + (2-d)d(1+t_-) -c(1+t_- + t_-^2)\right). \end{align}\]This has two unknowns in $d$ and $t_-,$ and we don’t know $d.$ However, we can optimize with respect to $t_-$ to find $t_-$ in terms of $d.$ Setting the derivative equal to zero and solving for $t_-(d)$ we get
\[t_-(d)= \frac{c(c-1) + d(2 - d)}{2c}.\]Plugging this back in, we get
\[P(J\,\text{wins}, J_1 < d) = \frac{\left((2-d)d-(1-c)c\right)\left(c(3+c)+(2-d)d\right)}{8cd}.\]When $S$ learns $d \leq J_1,$ they have two winning scenarios:
- neither $S$ nor $J$ reroll and $S$ wins. This means $t_+ < S_1 < 1$ and $d < J_1 < S_1.$
- $S$ rerolls and wins. This means $S_1 < t_+$ and $d < J_1$ and $J_1 < S_2.$
Put to integrals, these become
\[\begin{align} P(J\,\text{wins}, d < J_1) &= \int\limits_{t_+}^1\text{d}S_1 \int\limits_{d}^{S_1}\text{d}J_1 + t_+\int\limits_{d}^1\text{d}S_2 \int\limits_{d}^{S_2}\text{d}J_1 \\ &= \frac12\left(1 - 2d + t_+ +d^2t_+ - t_+^2\right) \end{align}\]Again, we can figure out $t_+$ in terms of $d$ by optimizing, and we get
\[t_+(d) = \frac12\left(1 + d^2\right).\]Plugging this back in, we get
\[P(J\,\text{wins}, d < J_1) = \frac18 (1-d)(5+d(2+d))\]We can add these results to get the overall probability that $S$ wins in terms of $d.$ Looking at the graph, it is monotonic decreasing as $d$ moves away from $c,$ so the optimal surveillance threshold is $d = c.$ This also means that $t_- = \tfrac12$ since there is no sliver where we’re uncertain if $J$ is rerolling. Plugging in $d=c,$ we get $t_+ = \tfrac14(5-\sqrt{5}).$
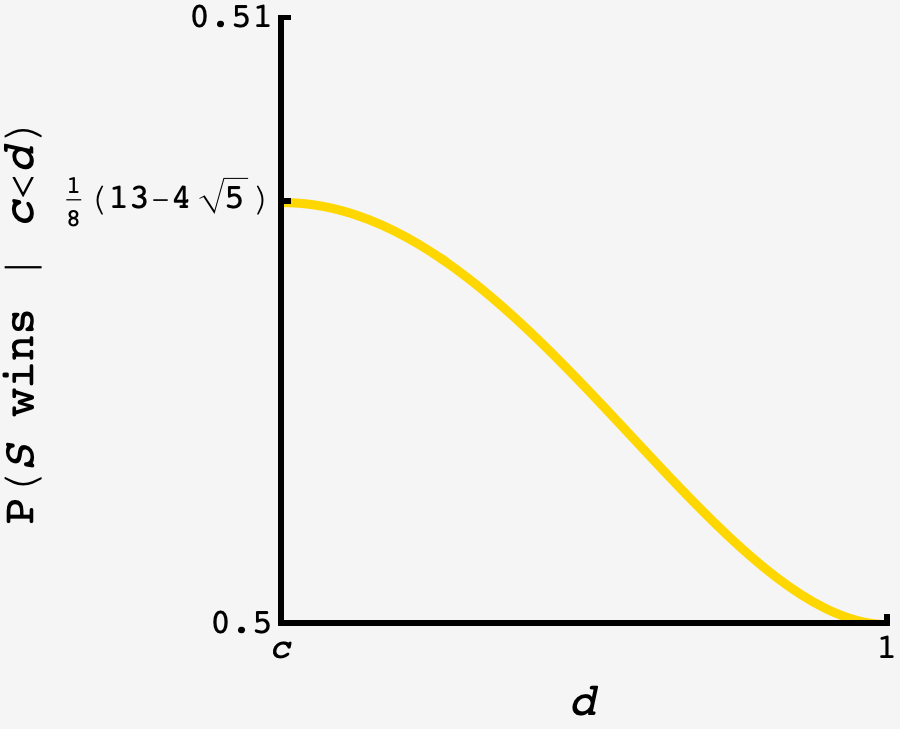
It should not be missed that the margins we’re playing with are very small, the range of win probability for $S$ stays between $50\%$ and $51\%.$
Level 3: the doubly perturbed game
Now, it’s $J$’s turn to have a secret threshold $h.$ They know that when their first roll is high, $S$ uses $t_+$ as a threshold. This means that there is already a region $c < J_1 < t_+$ where $J$ has the advantage, and we can foreclose on the possibility that $c < h.$
When $J_1 > c,$ $J$ can win by beating $S$’s first roll, or by beating their reroll. Adding up the probabilities, we get
\[\begin{align} P(J\,\text{wins}, c < J_1) &= \int\limits_{t_+}^1\text{d}J_1 \int\limits_{t_+}^{J_1}\text{d}S_1 \\ & \quad +\int\limits_h^1\text{d}J_1 \int\limits_0^{t_+}\text{d}S_1 \int\limits_0^{J_1}\text{d}S_2 \\ &= \frac{1-(1+c^2)t + t^2}{2} \\ &= \frac{1+2\sqrt{5}}{8} \\ &\approx 68.40\% \end{align}\]when $J_1 < c,$ we have all four cases active ($J$ winning on their first or second roll against $S$’s first roll or $S$’s reroll). adding up the probabilities, we get
\[\begin{align} P(J\,\text{wins}, J_1 < c) &= \int\limits_h^c\text{d}J_1 \int\limits_{t_-}^{J_1}\text{d}S_1 \\ & \quad +\int\limits_h^c\text{d}J_1 \int\limits_0^{t_-}\text{d}S_1 \int\limits_0^{J_1}\text{d}S_2 \\ & \quad +\int\limits_0^h\text{d}J_1 \int\limits_{t_-}^1\text{d}J_2 \int\limits_{t_-}^{J_2}\text{d}S_1 \\ & \quad +\int\limits_0^h\text{d}J_1 \int\limits_0^1\text{d}J_2 \int\limits_0^{t_-}\text{d}S_1 \int\limits_0^{J_2}\text{d}S_2 \\ &= \frac{c^2(1+t_-)-2ct_- +h((1+t_-)(1-h) + t_-^2)}{2c}. \end{align}\]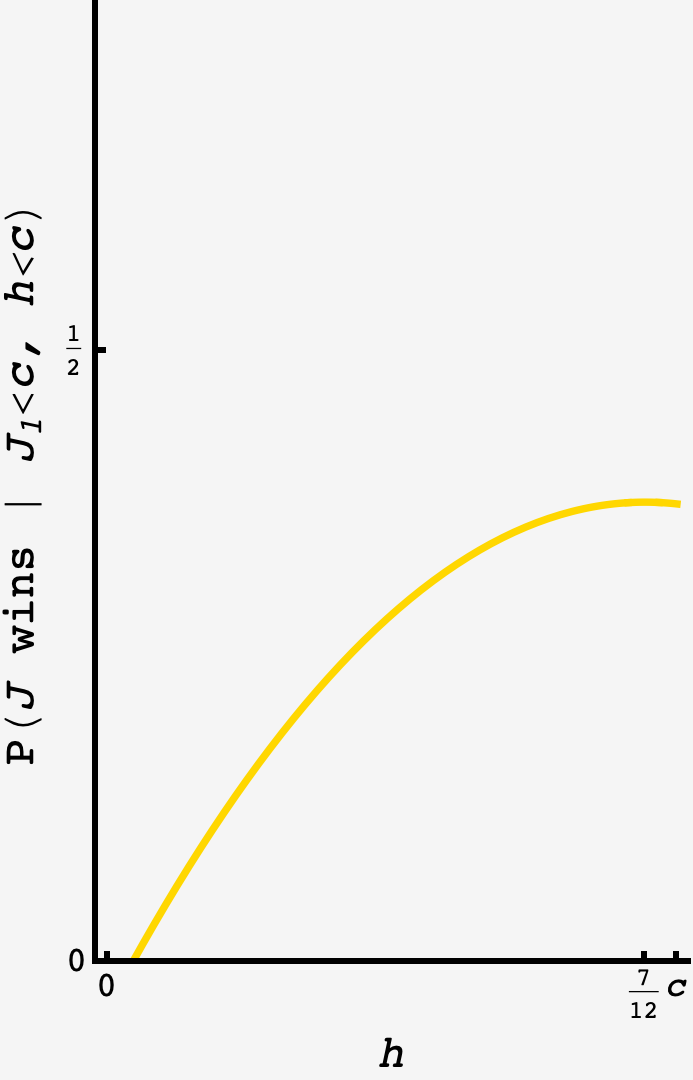
Optimizing for $h,$ we get
\[h = \frac12\frac{1+t_- +t_-^2}{1+t_-} = \frac{7}{12}.\]Plugging this back in, we get $P(J\,\text{wins}, J_1 < c) = \frac{193\sqrt{5}-287}{384} \approx 37.65\%.$ Putting it all together, the probability that $J$ wins under optimal play is
\[\begin{align} P(J\,\text{wins}) &= (1-c)P(J\,\text{wins} | c < J_1) + cP(J\,\text{wins}|J_1 < c) \\ &= \frac{1}{192} \left(229 - 60 \sqrt{5}\right) \\ &\approx 49.3937090364649\%, \end{align}\]which closes the gap from $100\%-50.70\% = 49.30\%$ by a full $9/100^\text{th}$s of a percent!
There’s an alternate interpretation which matched my initial read. In this version, $S$ can set $d$ after learning the result of their own first throw $S_1.$ In this scenario, a more significant advantage results and $J$’s optimized win probability ends up being $\tfrac{1}{72}\left(\tfrac{1515}{8}-69\sqrt{5}\right)\approx 48.73\%$