Question: You and your assistant are planning to irrigate a vast circular garden, which has a radius of $1$ furlong. However, your assistant is somewhat lackadaisical when it comes to gardening. Their plan is to pick two random points on the circumference of the garden and run a hose straight between them.
You’re concerned that different parts of your garden—especially your prized peach tree at the very center—will be too far from the hose to be properly irrigated.
On average, how far can you expect the center of the garden to be from the nearest part of the hose?
Extra credit As before, your assistant intends to pick two random points along the circumference of the garden and run a hose straight between them.
This time, you’ve decided to contribute to the madness yourself by picking a random point inside the garden to plant a second peach tree. On average, how far can you expect this point to be from the nearest part of the hose?
Solution
Because of the radial symmetry, we can ignore the exact orientation of the hose and focus on the angle between the two random points on the perimeter. If the smaller angle made by the two points is $\theta$ then the distance from the hose to the center will be $h_\theta = \cos\frac12\theta.$
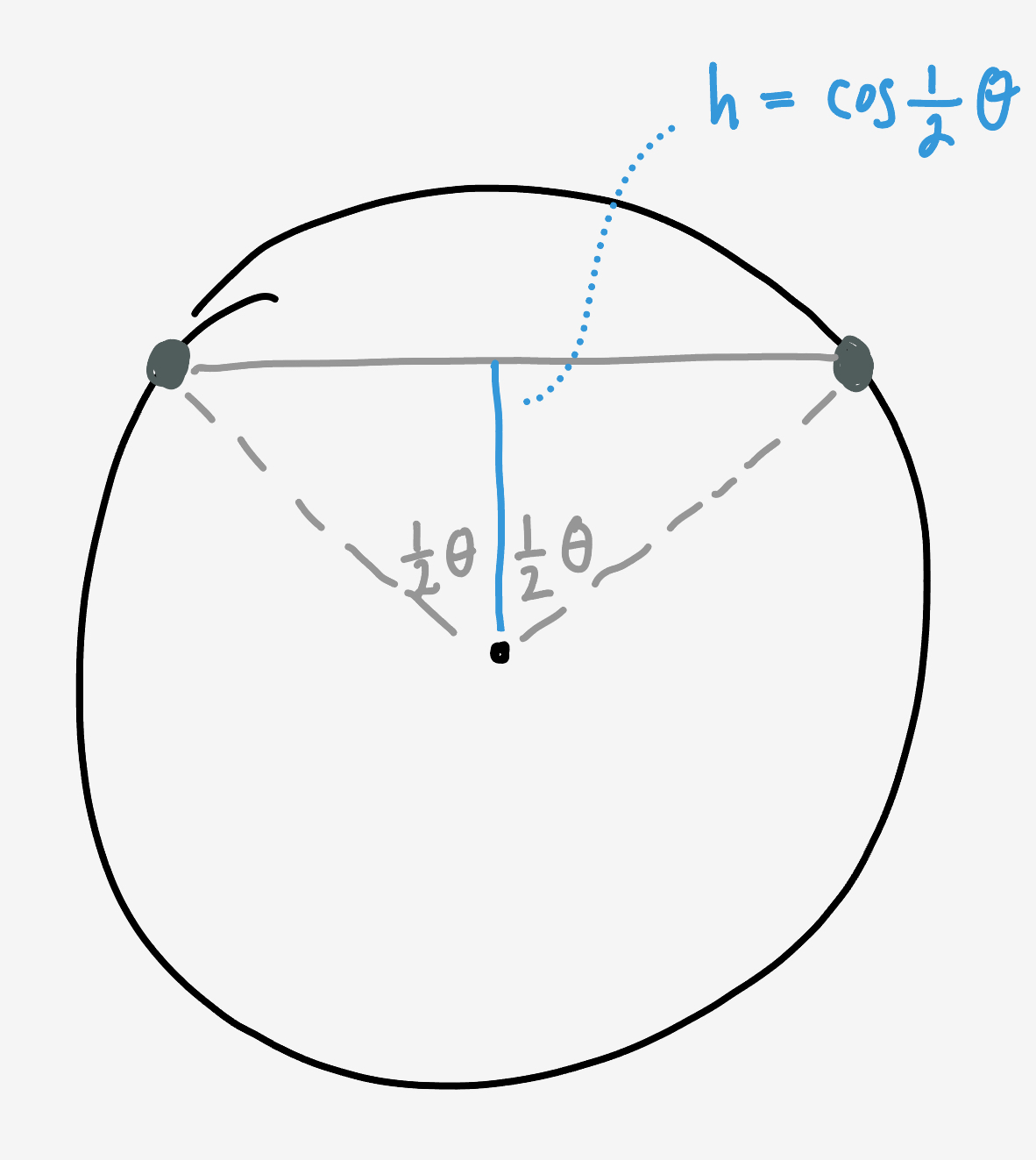
The placement of the second point relative to the first is uniformly random, so the probability distribution on $\theta$ is uniform from $0$ to $\pi.$
Averaging the distance over $\theta$ we get an expected hose to tree distance of
\[\begin{align} \int\limits_0^\pi \text{d}\theta\, p_\theta h_\theta &= \frac1\pi \int_0^\pi \text{d}\theta\, \cos\frac12\theta \\ &= \frac{2}{\pi}\left[\sin\frac12\pi -\sin0\right] \\ &= \frac{2}{\pi} \\ &\approx 0.63661977\ldots \end{align}\]Extra credit
Now the tree can be anywhere.
As before, we can ignore the orientation of the hose. Wherever the point lands, its distance to the closest point on the hose is the vertical separation between the line of the hose and the line through the point that’s parallel to the hose.
The probability a point lands distance $y$ from the center is proportional to the width of the parallel at that height. Because all points on the circle satisfy $x^2 + y^2 = 1$, the width of the strip is ${2x = 2\sqrt{1-y^2}}.$
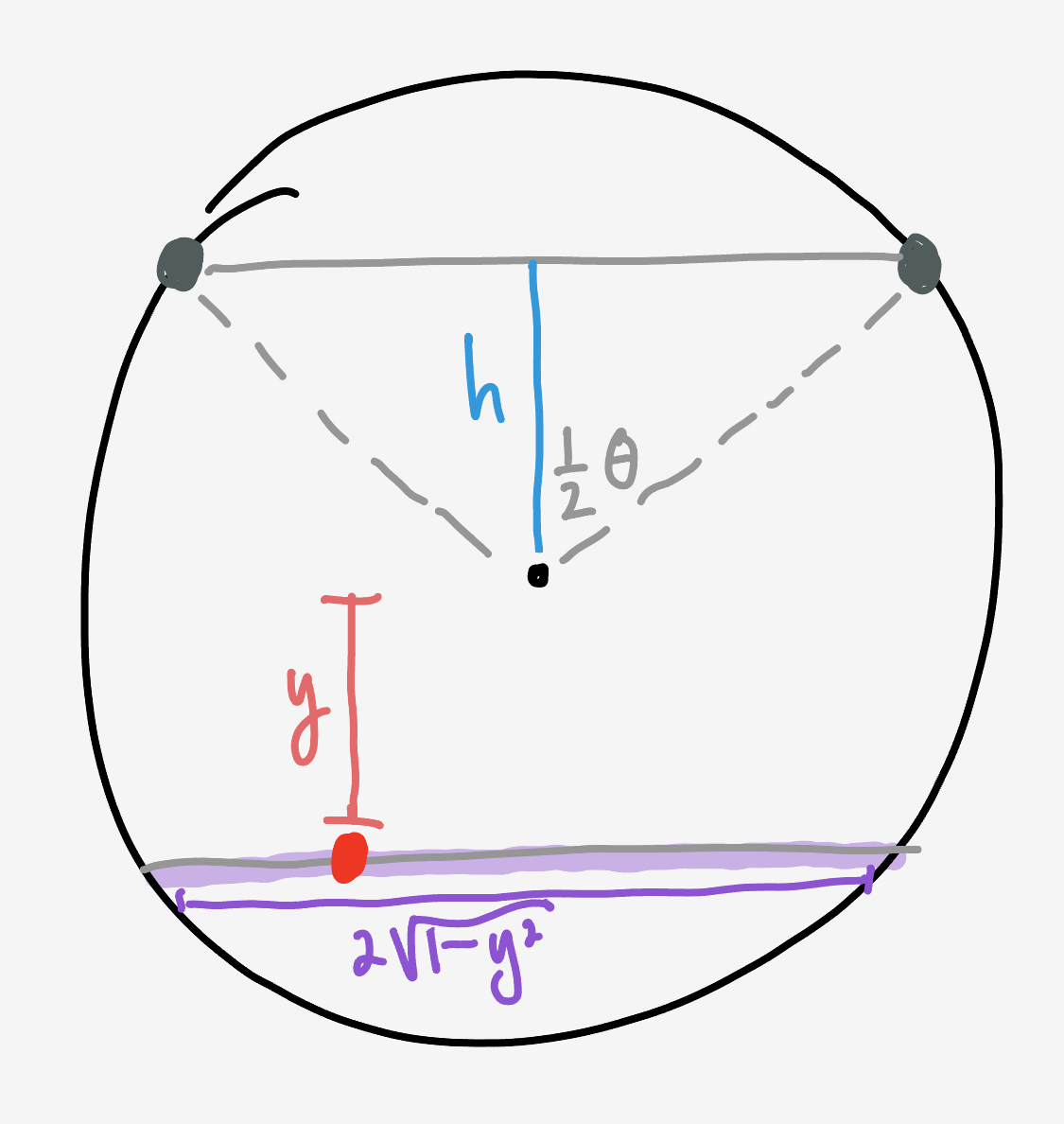
The integral of this strip over $y$ is just the area of the circle, so the distribution on $y$ is $p_y = \frac{2}{\pi}\sqrt{1-y^2}.$
The average distance for a given $h$ is then simply
\[\begin{align} \langle d_h\rangle &= \int_{-1}^1 \text{d}y\, p_y \lvert y-h\rvert \\ &= \frac{2}{\pi} \int_h^1 \text{d}y\, \sqrt{1-y^2}(y-h) + \frac{2}{\pi} \int_{-1}^h \text{d}y\, \sqrt{1-y^2} (h-y) \\ &= \frac{2}{\pi}\left[\frac{1}{3} \sqrt{1-h^2} \left(h^2+2\right)+h \sin ^{-1}h\right] \end{align}\]Plugging in $h = \cos\frac12\theta,$ we can average over $\theta$ to get the unqualified expected tree to hose distance:
\[\begin{align} \langle d\rangle &= \int_0^\pi\text{d}\theta\, p_\theta \langle d_\theta\rangle \\ &= \frac{1}{\pi} \int_0^\pi\text{d}\theta \left[\frac{1}{6} \left(\cos\theta + 5\right)\sin\frac{1}{2}\theta + \cos\frac{1}{2}\theta \sin ^{-1}\left(\cos\frac{1 }{2}\theta\right)\right] \\ &= \frac{64}{9\pi^2} \approx 0.7205061\ldots \end{align}\]It is tantalizing to wish for a simpler path to $(8/3\pi)^2,$ but as yet none has revealed itself.