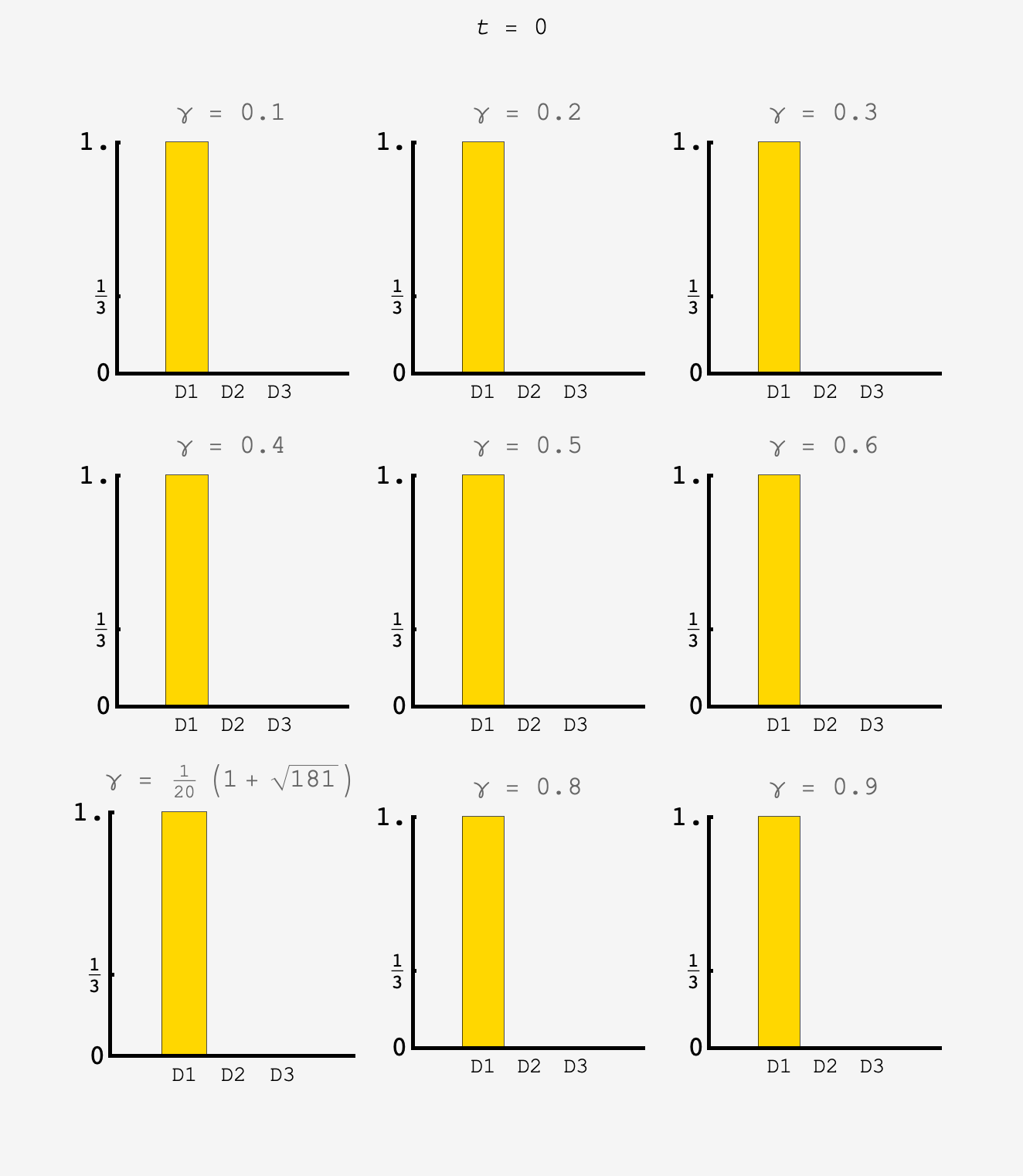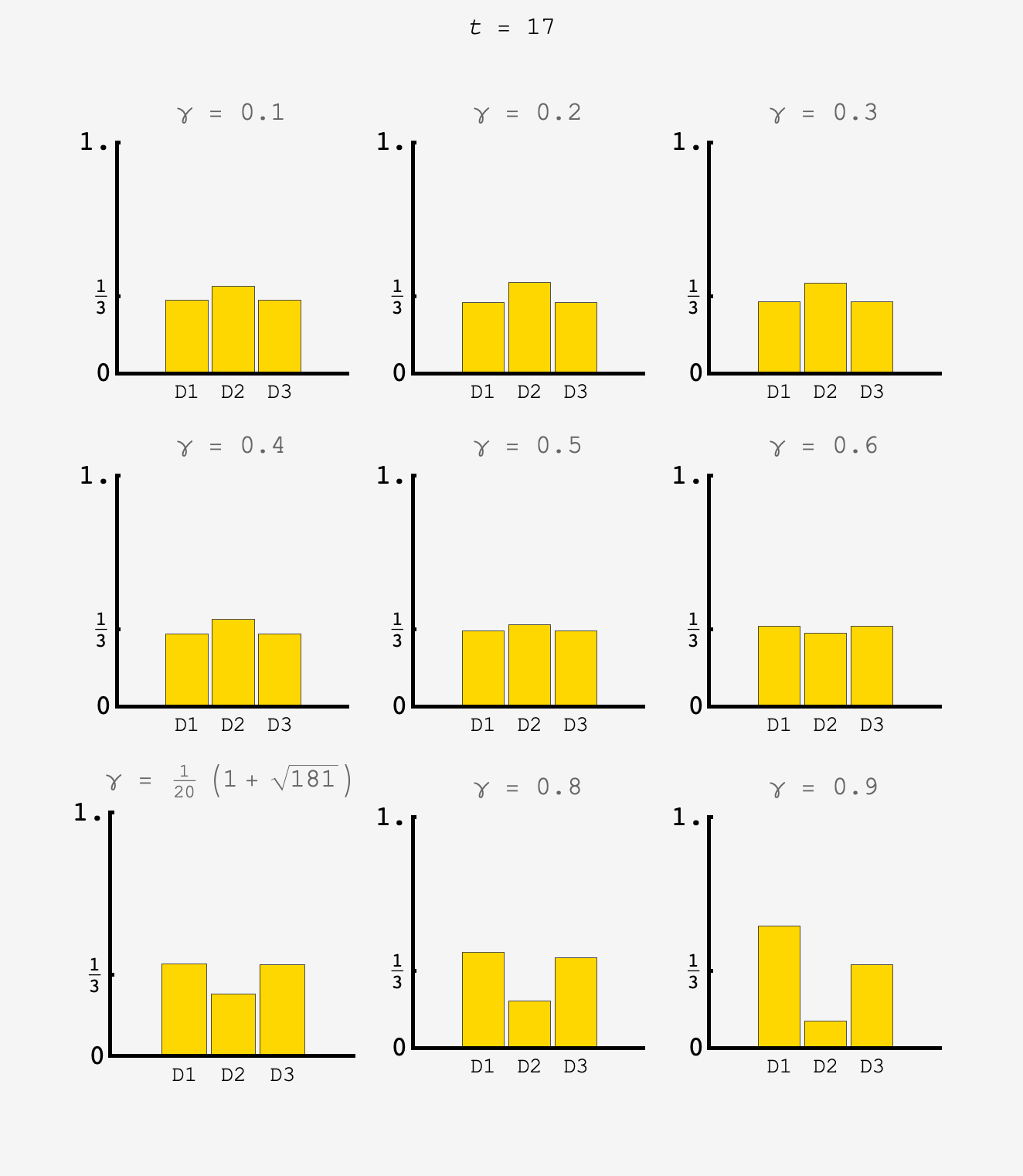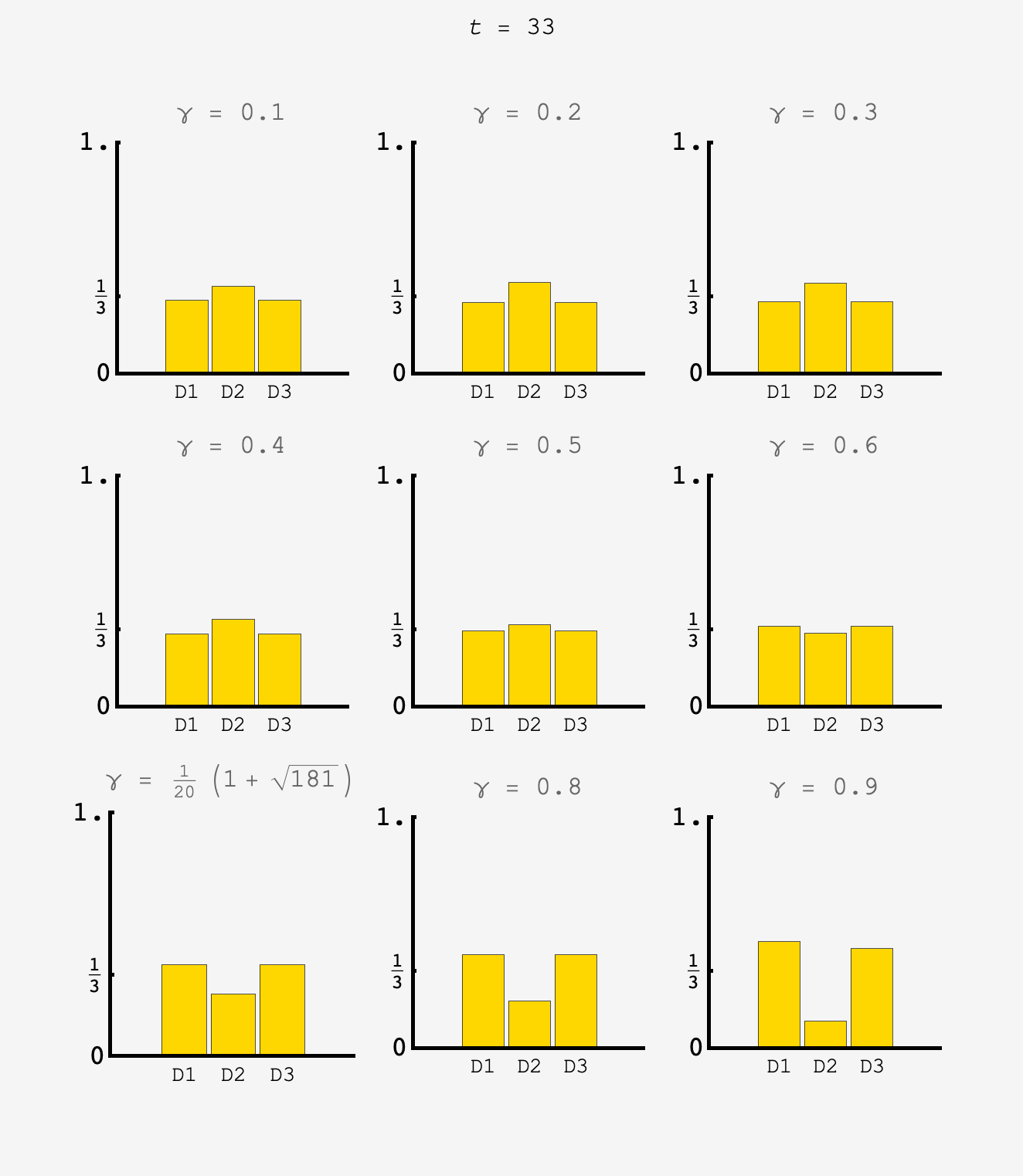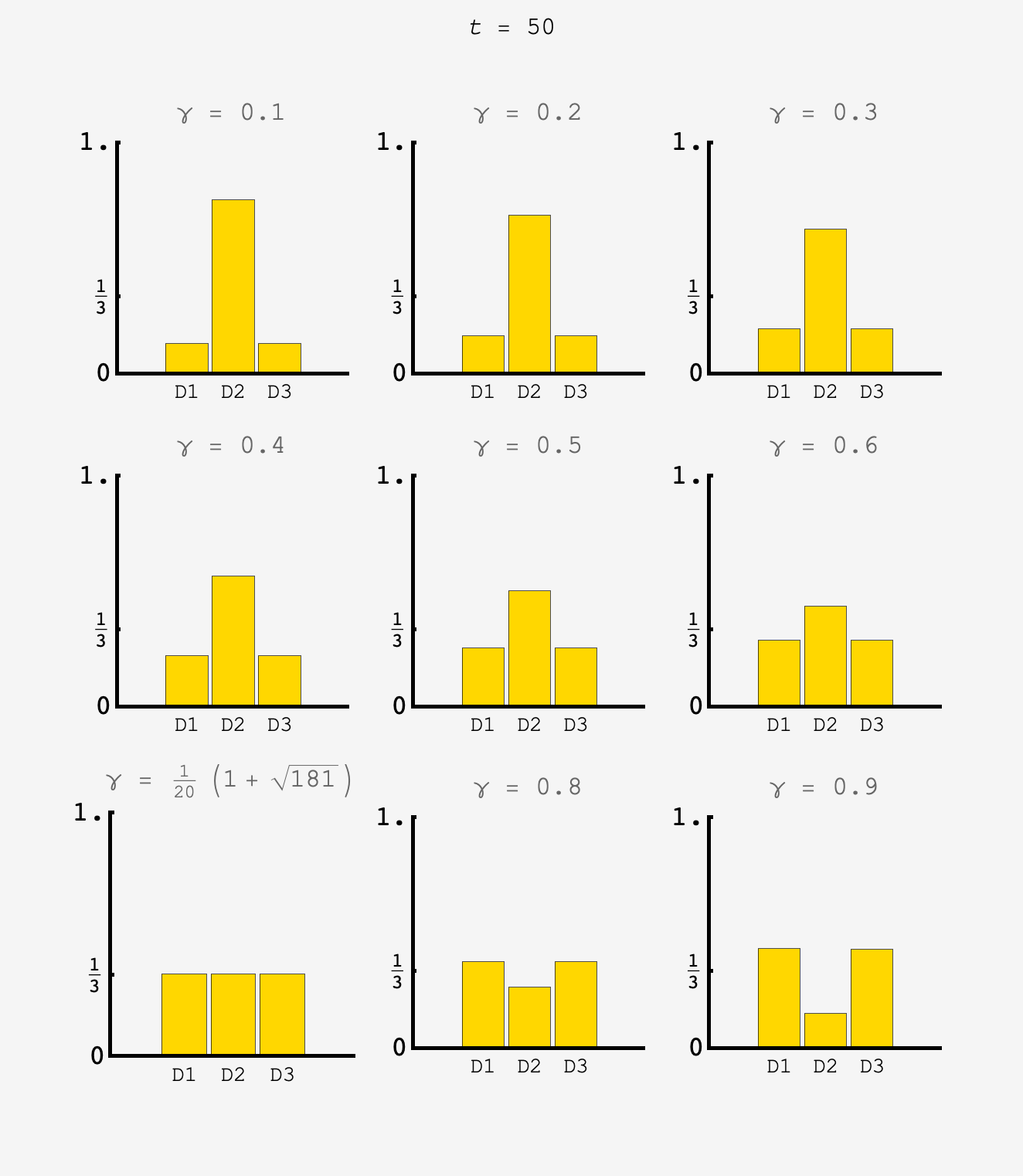Question: You are a producer on a game show hosted by Randy “Random” Hall (no relation to Monty Hall). The show has three doors labeled 1 through 3 from left to right, and behind them are various prizes.
Contestants pick one of the three doors at which to start, and then they press an electronic button many, many times in rapid succession. Each time they press the button, they either stay at their current door or move to an adjacent door. If they’re at door 2 and move to an adjacent door, that new door will be 1 or 3 with equal probability.
Randy has decided that when a contestant presses the button while at door 2, there should be a 20 percent chance they remain at door 2.
As the producer, you want the chances of a contestant ultimately winding up at each of the three doors to be nearly equal after many button presses. Otherwise, mathematicians will no doubt write you nasty letters complaining about how your show is rigged.
If a contestant presses the button while at door 1 (or door 3), what should the probability be that they remain at that door?
Extra credit: Randy has an updated suggestion for how the button should behave at door 2. What hasn’t changed is that if a contestant at door 2 and moves to an adjacent door, that new door will be 1 or 3 with equal probability.
But this time, on the first, third, fifth, and other odd button presses, there’s a 20 percent the contestant remains at door 2 (if they happen to be there). On the second, fourth, sixth, and other even button presses, there’s a 50 percent chance the contest remains at door 2 (again, if they happen to be there).
Meanwhile, the button’s behavior at doors 1 and 3 should in no way depend on the number of times the button has been pressed.
As the producer, you want the chances of winding up at each of the three doors—after a large even number of button presses— to be nearly equal.
If a contestant presses the button while at door 1 (or door 3), what should the probability be that they remain at that door?
Solution
The probability to end up at a place is found by all the ways we can get there.
Standard credit
A contestant can be at door $1$ at time $(t+1)$ because they were already there and stayed put or because they came from door $2$
\[P_1(t+1) = \gamma P_1(t) + \frac{4}{10}P_2(t).\]Likewise, a contestant can be at door $2$ at time $(t+1)$ because they were already there and stayed put or because they came from doors $1$ or $3$
\[P_2(t+1) = (1-\gamma)\left[P_1(t) + P_3(t)\right] + \frac{2}{10}P_2(t).\]The equation for door $3$ has the same form as for door $1.$ (we don’t actually need all of these equations, but it’s good setup for the extra credit where we will)
We’re trying to arrange $\gamma$ so that the probability of being at any of the three doors is equal, so the first equation becomes
\[1 = \gamma + \frac{4}{10}\]or $\gamma = \frac{6}{10}. $
Simulating over a range of $\gamma$ we see that the $\gamma=6/10$ system settles down to the equiprobable state after about 10 button presses.
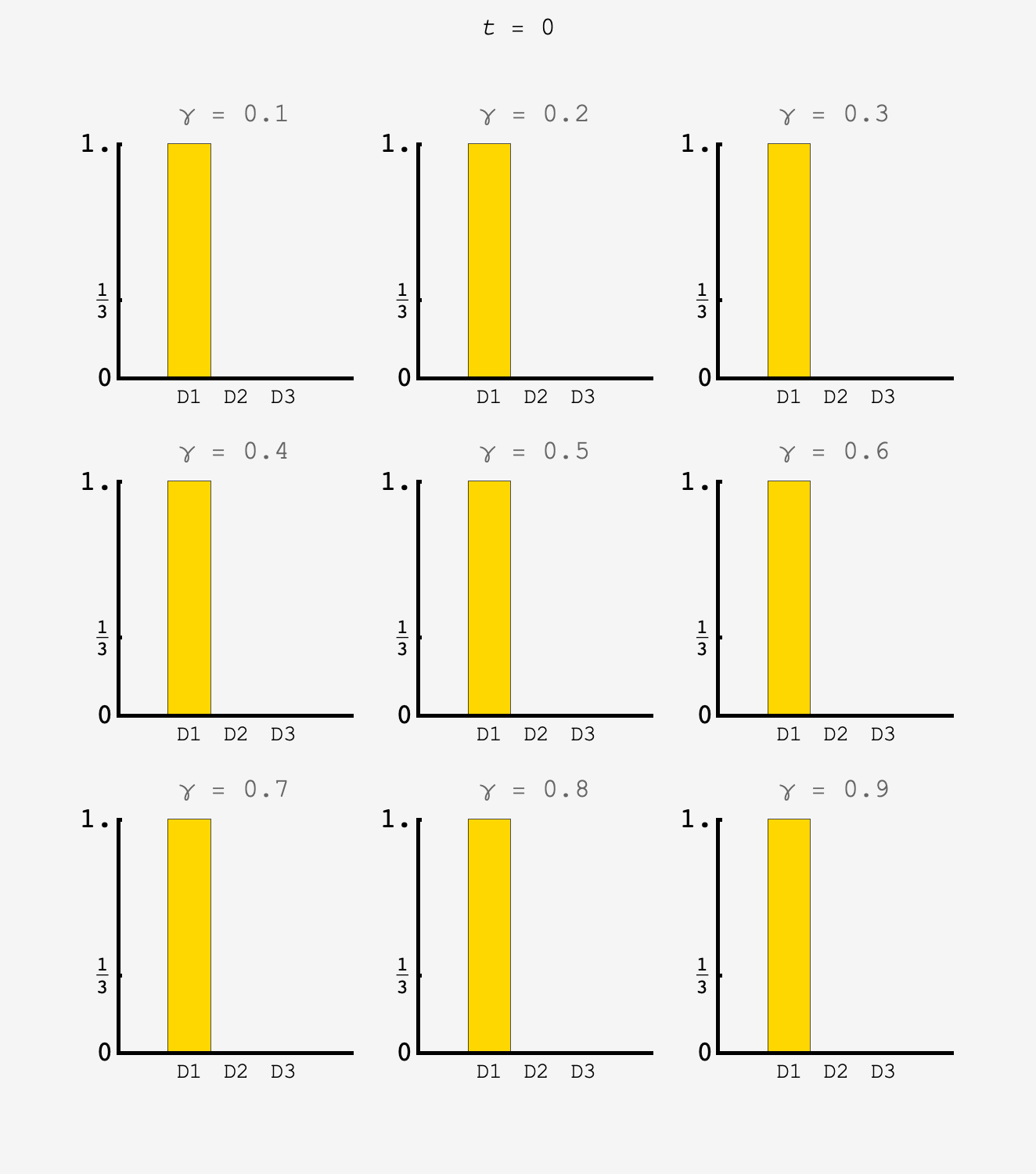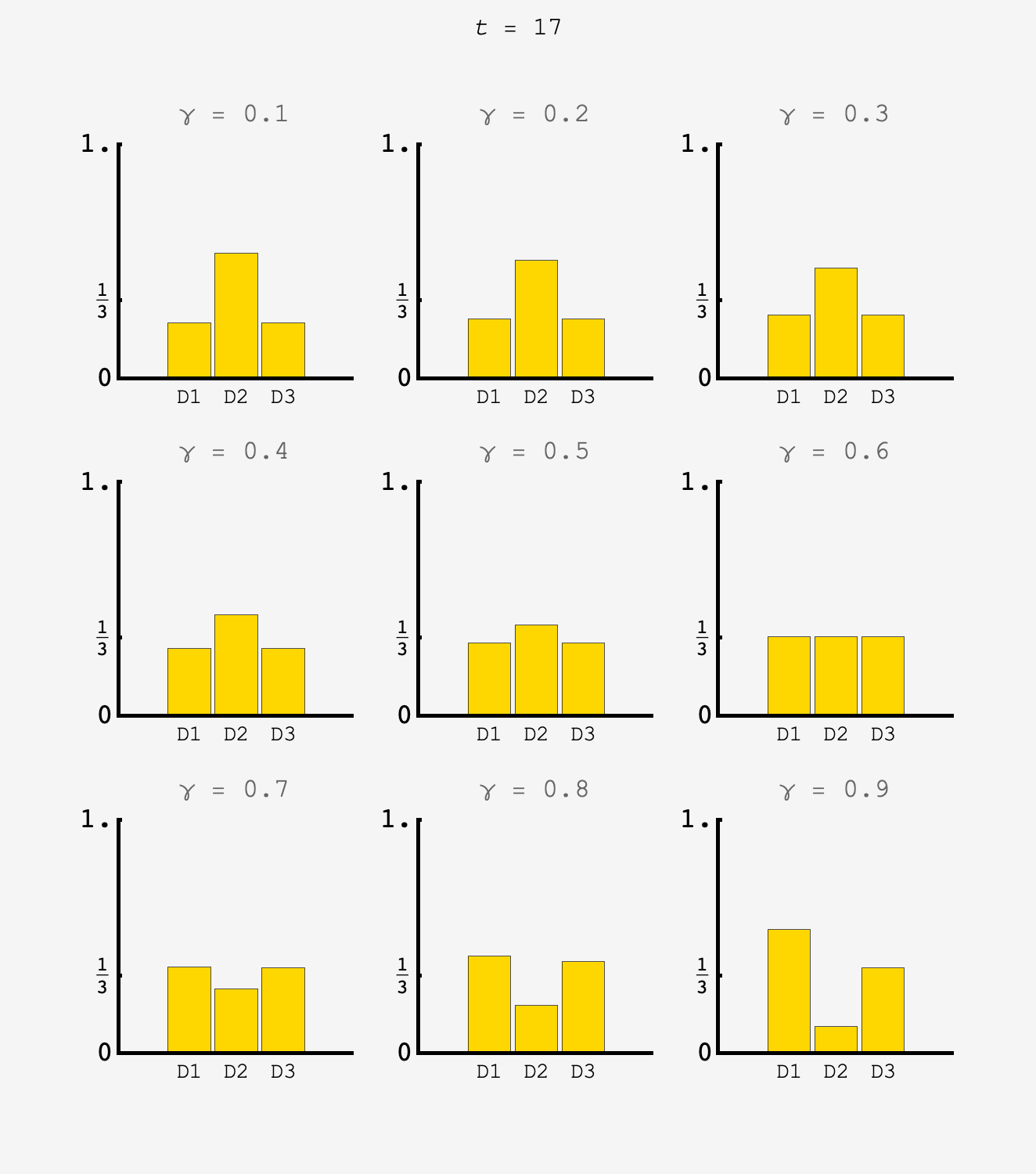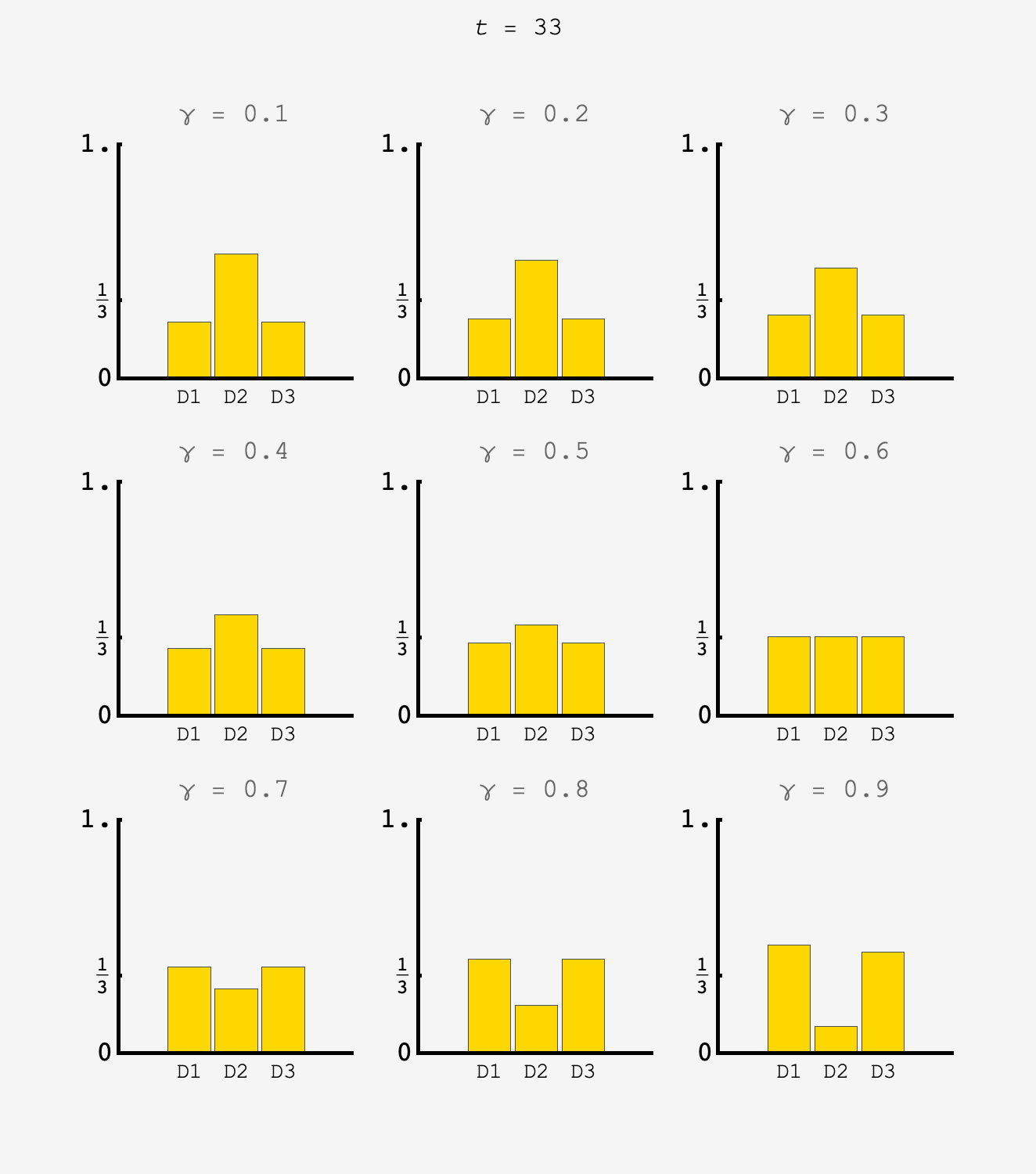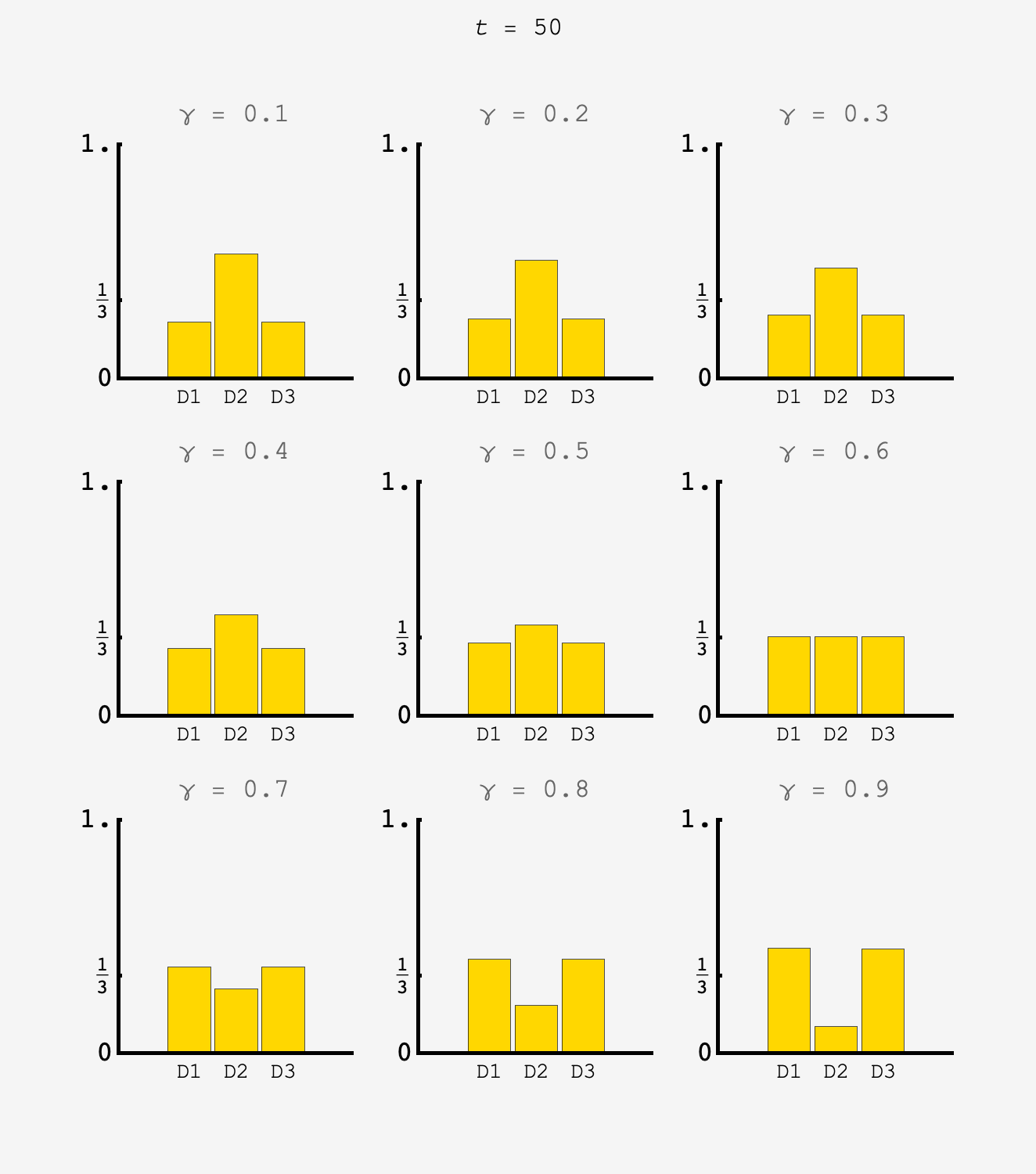
Extra credit
Now, the probability to remain at door $2$ flip flops between $\frac{2}{10}$ and $\frac12.$ Because the effective rate of staying at door $2$ is higher, we should expect the contestant to stay at doors $1$ and $3$ more often as well to compensate, so $\gamma^\prime > \gamma.$
The transition from an even turn to an odd turn has the same relationships that we worked above, so
\[\begin{align} P_1^\text{odd} &= \gamma^\prime P_1^\text{even} + \frac{4}{10}P_2^\text{even} \\ P_2^\text{odd} &= \left(1-\gamma^\prime\right) \left[P_1^\text{even} + P_2^\text{even}\right] + \frac{2}{10}P_2^\text{even} \\ P_3^\text{odd} &= \gamma^\prime P_3^\text{even} + \frac{4}{10}P_2^\text{even} \end{align}\]The transition from odd to even also has the same structure but with a new rate for staying at door $2$
\[\begin{align} P_1^\text{even} &= \gamma^\prime P_1^\text{odd} + \frac14 P_2^\text{odd} \\ P_2^\text{even} &= \left(1-\gamma^\prime\right) \left[P_1^\text{odd} + P_2^\text{odd}\right] + \frac12 P_2^\text{odd} \\ P_3^\text{even} &= \gamma^\prime P_3^\text{odd} + \frac14 P_2^\text{odd} \end{align}\]We can plug the first set of equations into the equation for door $1$ to get
\[P_1^\text{even} = \gamma^\prime\left(\gamma^\prime P_1^\text{even} + \frac{4}{10}P_2^\text{even}\right) + \frac14\left(\left(1-\gamma^\prime\right) \left[P_1^\text{even} + P_2^\text{even}\right] + \frac14\frac{2}{10}P_2^\text{even}\right).\]Since the aim is for these probabilities to become equal, this equation becomes
\[1 = {\gamma^\prime}^2 + \gamma^\prime\frac{4}{10} + 2\frac14\left(1-\gamma^\prime\right) + \frac14\frac{2}{10}\]or
\[0 = {\gamma^\prime}^2 -\frac{1}{10}\gamma^\prime -\frac{9}{20}.\]That has positive root $\frac1{20}\left(1+\sqrt{181}\right) \approx 0.7226812$
With $\gamma^\prime$ in hand, we can use the system to predict the distribution on odd numbered steps: we should have $P_1^\text{odd} = P_3^\text{odd} = (\gamma^\prime +\frac{4}{10})\times\frac13 \approx 0.37422707$ and $P_2^\text{odd} = \left[2(1-\gamma^\prime) + \frac{2}{10}\right]\times\frac13 \approx 0.25154587$ which matches simulation.