Question:
The Artificial Automaton Athletics Association (Quad-A) is at it again, to compete with postseason baseball they are developing a Robot Baseball competition. Games are composed of a series of independent at-bats in which the batter is trying to maximize expected score and the pitcher is trying to minimize expected score.
An at-bat is a series of pitches with a running count of balls and strikes, both starting at zero. For each pitch, the pitcher decides whether to throw a ball or strike, and the batter decides whether to wait or swing; these decisions are made secretly and simultaneously. The results of these choices are as follows.
- If the pitcher throws a ball and the batter waits, the count of balls is incremented by $1.$
- If the pitcher throws a strike and the batter waits, the count of strikes is incremented by $1.$
- If the pitcher throws a ball and the batter swings, the count of strikes is incremented by $1.$
- If the pitcher throws a strike and the batter swings, with probability $p$ the batter hits a home run and with probability $(1-p)$ the count of strikes is incremented by $1.$
An at-bat ends when either:
- The count of balls reaches $4,$ in which case the batter receives $1$ point.
- The count of strikes reaches $3,$ in which case the batter receives $0$ points.
- The batter hits a home run, in which case the batter receives $4$ points.
By varying the size of the strike zone, Quad-A can adjust the value $p,$ the probability a pitched strike that is swung at results in a home run. They have found that viewers are most excited by at-bats that reach a full count, that is, the at-bats that reach the state of three balls and two strikes. Let $q$ be the probability of at-bats reaching full count; $q$ is dependent on $p.$ Assume the batter and pitcher are both using optimal mixed strategies and Quad-A has chosen the $p$ that maximizes $q.$ Find this $q,$ the maximal probability at-bats reach full count, to ten decimal places.
Solution
the big idea here is that batters and pitchers are motivated by expectation value. in each count, they will do what maximizes their EV, defined for the batter as the probability weighted average of $0$ (out), $1$ (walk), and $4$ (homerun). that let’s us work backward from the goal states to find the values of each intermediate state. however, those decisions determine the probabilities of forward transitions from the blank count $(0,0)$ to any of the terminal states. so, we will work backward to work forwards. at the end, we will still have the undetermined parameter $p$ set by the scheming league office. they will set it to whatever value maximizes the probability of the full count state, in the wake of the decision structure of the players.
the value of count $(b,s)$ is the average value of the counts it can move to. a strike can be added if the pitcher throws a strike and the batter doesn’t swing, or if the pitcher throws a ball and the batter swings, or if the pitcher throws a strike and the batter misses. a ball can be added if the pitcher throws one and the batter doesn’t swing. finally, the batter can walk or hit a homerun which have values $1$ and $4$.
\[\begin{align} V(b,s) &= P_\text{strike}P_\text{swing}pV_\text{HR} \\ \,& + \left[P_\text{strike}(1-P_\text{swing}) + (1-P_\text{strike})P_\text{swing} + P_\text{strike}P_\text{swing}(1-p) \right]V(b,s+1) \\ &+ (1-P_\text{strike})(1-P_\text{swing})V(b+1,s) \end{align}\]with any $4$-ball count equal to $1$ and any $3$-strike count equal to zero.
\[\begin{align} V(4,x) &= 1 \\ V(x,3) &= 0 \end{align}\]this is a recursion relating the value of each count to the value of the outcomes it can lead to. but at each step the pitcher and batter can set the probabilities however they like, so they’ll change with the count.
however, we know the batter is trying to maximize the value of the at bat while the pitcher is trying to minimize it. this means the batter will pick $P_\text{swing}$ so that the value is indifferent to a change in $P_\text{strike}$ so they will set according to
\[\frac{\partial V(b,s)}{\partial P_\text{strike}} = 0,\]and vice versa for the pitcher
\[\frac{\partial V(b,s)}{\partial P_\text{swing}} = 0.\]somewhat surprisingly, the value function is symmetric with respect to $P_\text{strike}$ and $P_\text{swing},$ so they’ll set their probabilities to the same equilibrium value. solving these, we can find this optimal probability in terms of the expected values of the future states.
this gets us
\[P_\text{strike}(b,s) = P_\text{swing}(b,s) = \frac{V(b,s+1) - V(b+1,s)}{pV(b,s+1) - V(b+1,s)-pV_\text{HR}}\]plugging this back in to the recursion, we get
\[V(b,s) = \frac{\left(pV_\text{HR} + (1-p)V(b,s+1)\right)V(b+1,s)-V(b,s+1)^2}{pV_\text{HR}+(1-p)V(b,s+1) + V(b+1,s)]}\]which lets us compute the expected value of each state.
Vhomerun = 4;
V[4, _] = 1;
V[_, 3] = 0;
V[b_, s_] :=
V[b, s] =
(-V[b, 1 + s]^2 + (p Vhomerun - (-1 + p) V[b, 1 + s]) V[1 + b, s]) /
(p Vhomerun - (1 + p) V[b, 1 + s] + V[1 + b, s]);
plotting this, we can see how the expected value to the batter evolves in each count (equivalently, the negative value to the pitcher). as we move from $(0,0)$ to $1, 2$ and $3$ balls, the batter becomes near certain to get $1$ for all $p \gtrapprox 0.4.$ likewise, as we add strikes, the curve bends down quite a bit, so that an $(0,2)$ count has a max of $1/2$ when $p=1.$
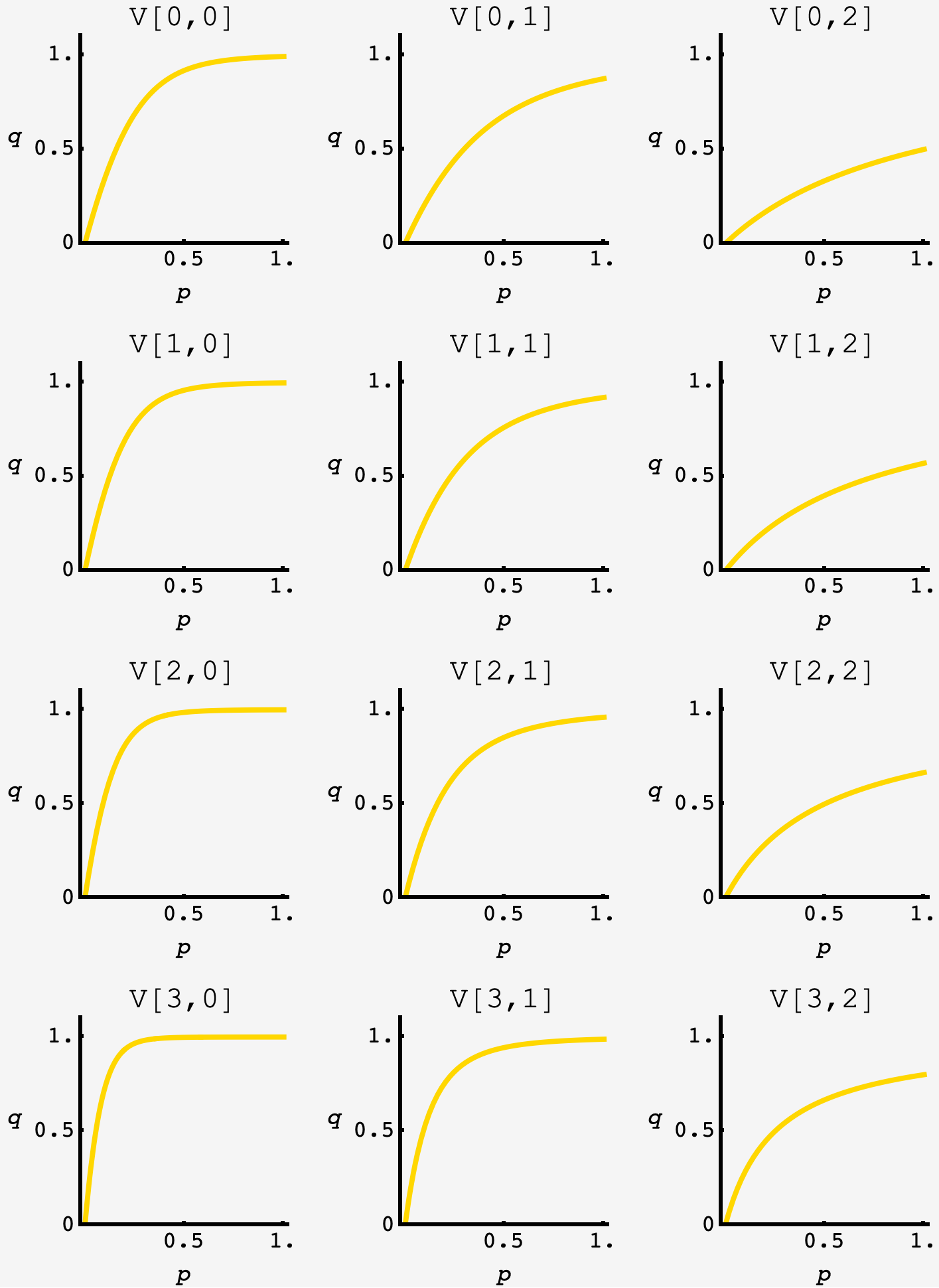
now, we can use these values to find the probabilities of forward propagation.
the probability $W\left[b,s\right]$ that we get to a particular state is the chance that we get to each predecessor times the chance they transition to the current state. since walks, homeruns, and outs are terminal states that can’t transition to the full count, we can ignore them for this purpose. also, every count is guaranteed to start at $(0,0)$ so that $W\left[0,0\right]=1.$
the transitions are governed by the probabilities we just found, we just need to turn things round and track the transitions in the forward direction:
\[\begin{align} W(b,s) &= (1-P_\text{strike}(b-1,s))(1-P_\text{swing}(b-1,s))W(b-1,s) \\ &\, + [P_\text{strike}(b,s-1)P_\text{swing}(b,s-1)(1-p) \\ &\, +P_\text{strike}(b,s-1)(1-P_\text{wing}(b,s-1)) \\ &+(1-P_\text{strike}(b,s-1))P_\text{swing}(b,s-1)]W(b,s-1). \end{align}\]with
\[W(-1,x) = W(x,-1) = 0\]and
\[W(0,0) = 1.\]pstrike[b_, s_] := (
V[b, 1 + s] - V[1 + b, s])/(-p Vhomerun + V[b, 1 + s] + p V[b, 1 + s] - V[1 + b, s]
);
pswing[b_, s_] := pstrike[b,s];
W[0, 0] = 1;
W[-1, _] = 0;
W[_, -1] = 0;
W[b_, s_] :=
W[b, s] =
((1 - pstrike[b - 1, s]) (1 - pswing[b - 1, s])) W[b - 1, s] +
(pstrike[b, s - 1] pswing[b, s - 1] (1 - p) +
pstrike[b,
s - 1] (1 - pswing[b, s - 1]) + (1 -
pstrike[b, s - 1]) pswing[b, s - 1]) W[b, s - 1]
;
recursing, we can get the wondrous expression for $W(3,2):$
\[\tiny\frac{(4 p+1)^2 \left(5851619180814139514742531684248049334443899564851200 p^{88}+236394443118927209884008137796713228019031460108304384 p^{87}+4724404406019468778040993414020409979753509561347080192 p^{86}+62279399393231087900518921966880114364461447471186313216 p^{85}+609229556640332213513856177342799597182548210833164337152 p^{84}+4717188960953307112887848481026807851294238658835865665536 p^{83}+30114554888931987635547158063814519920483860324994764505088 p^{82}+163038281078792933422476610583288732585114454938108464988160 p^{81}+764135332527586242960193606967486890190643578703281079189504 p^{80}+3149550756294366024600712932710728655878185187587413885583360 p^{79}+11558673410546233433292400596505126852478775734804120359403520 p^{78}+38150405229077377287092013897858017185141243581662280844050432 p^{77}+114185120480009608242715694011885565035104850103586182205014016 p^{76}+312065684473927300744463629611555859175994037831480826923057152 p^{75}+783363998674200392138106411389848665563640918036334957125697536 p^{74}+1815340798398520674025570251240685434333569792105702844530688000 p^{73}+3900635300005116515157417632641386933551859279929255091190628352 p^{72}+7801222856767342635036237682545105719305459265106346512280977408 p^{71}+14571684662618224130569086618940176949625113532569990121115353088 p^{70}+25496446226938829042107043828599235806707496336833125387172052992 p^{69}+41901913621720059699031486548282415749749602906003050524124905472 p^{68}+64835432368806823179521975955068289943827581202581692089964167168 p^{67}+94656442533215063419555294303892237741157153977499270017779236864 p^{66}+130644237284955204326196872516579778424177576722677973352030666752 p^{65}+170763515327756126194462746025981762243012530702644661928769617920 p^{64}+211716991372582219562631578375186196605046049570533756190857363456 p^{63}+249344391402308855434129431191193344838866375607226253323416895488 p^{62}+279316921440520444519900412383836130193440813387248980155315519488 p^{61}+297966738806262180163634740080494277714861360672277413718910828544 p^{60}+303028760823563630646520076528248743660696341264739071402031710208 p^{59}+294086901009323946380015905930279363768598263286400870422295871488 p^{58}+272605575519271045709760319265754062434085190963121160060298854400 p^{57}+241555410235080111029249286006250754757482315665848962346525917184 p^{56}+204759727875669472901665749124570453735537780652337399656966258688 p^{55}+166153752422729784552353668508689066088806609614895755315961135104 p^{54}+129144842692893924712405489069474059208391074575027396404614004736 p^{53}+96201510995351430383837450606993212620745126236021560408134385664 p^{52}+68712525709732284210019653026414693940244813154437219745305460736 p^{51}+47078910411897556764381656286982688320571632150482789676842221568 p^{50}+30954071103367616036814050791050175974035920029789738724440932352 p^{49}+19536759937611821927810701079938238189276155217070220313150619648 p^{48}+11840011172851102543549092714048645092331866938483443381634596864 p^{47}+6891559030749546025146122344026145461485896658071552420252483584 p^{46}+3853272580362210221812707468815991000508852373323421657145016320 p^{45}+2069905173292267524575878827888256619847406919656212324302192640 p^{44}+1068370737697566067335444360436400215545536990638924996445995008 p^{43}+529867887025076182349760541727659786885538877368290924069650432 p^{42}+252517510203079940995904842161617515360629169367770835082805248 p^{41}+115632182184035297838922904435592738005956277575969137097703424 p^{40}+50873886696210923783665590134213782594515678374884524007882752 p^{39}+21502352954329271464050175657670197888463388123326827179540480 p^{38}+8729262819032414997741316187155691445202938816974152777334784 p^{37}+3403097613090432870551681082115704090433775056668505537511424 p^{36}+1273677625016233407433782381834880442883183807998535860748288 p^{35}+457502239926124019680074047581347930932403342581523901317120 p^{34}+157656524508044403336360394022571585480454978825941085323264 p^{33}+52098692859125382584494463563060436622795737926310339346432 p^{32}+16501448264401213025536528988432510344851790436295659814912 p^{31}+5006716463036055332817014694249292506233851261949705797632 p^{30}+1454266095492389376842033262204256874616563960303362572288 p^{29}+404096648376541822239734921785904791437344253948766863360 p^{28}+107332416252712841936599285936238767096028688550913507328 p^{27}+27226660676718095317373565706460769073404170245741867008 p^{26}+6589383588834301635989746857216577617701230938357018624 p^{25}+1519854560546899430834226741054614604023056564105362432 p^{24}+333680699865567089812113610282591691980805386306615296 p^{23}+69636245900731002540530750394933237193220463191040000 p^{22}+13792680799240254671245893113699356088143172255385600 p^{21}+2588367831276093941671494612730830389204056219281408 p^{20}+459337481681611393180097711061241100332543848013824 p^{19}+76917827690896028287310458976620358303375367537408 p^{18}+12124153389408568417747879396638627198591607977216 p^{17}+1793924393372172773025139424623092129628841448000 p^{16}+248380646762520581746196315306561311853959033728 p^{15}+32064656324451386720619307977242562199827922560 p^{14}+3843492606949233557382925347924067637949144576 p^{13}+425716095090588383007436480534549102233981312 p^{12}+43326320892959201193064738185866055932881728 p^{11}+4024485355010303708567804402776817157306640 p^{10}+338455723263469562278334277461520266826816 p^9+25519168980471847744122846052126032772480 p^8+1704154757128887235833394339912071975296 p^7+99239500033477174973527499125926000832 p^6+4937739159886663676504808418855345360 p^5+204122498158521002818899593335477456 p^4+6731718371423293845994175209036560 p^3+166067158354603474266629725080000 p^2+2724514466821006612679936470488 p+22298719092129794448503164065\right)}{16 (p+1)^4 \left(20736 p^7+79488 p^6+136368 p^5+138696 p^4+90288 p^3+37152 p^2+8856 p+965\right)^2 \left(3833759992447475122176 p^{39}+63257039875383339515904 p^{38}+510076442328480387956736 p^{37}+2681204834162458547453952 p^{36}+10339554929584732775645184 p^{35}+31210348782550962690588672 p^{34}+76829059222172954838171648 p^{33}+158652346028074055699005440 p^{32}+280540834090792596384251904 p^{31}+431461184344320874200956928 p^{30}+584189702552751413425864704 p^{29}+703103995955353785862717440 p^{28}+758072938264354073001590784 p^{27}+736829995287139842323644416 p^{26}+648964134602735235177775104 p^{25}+520098953861184169126920192 p^{24}+380561296454266300251439104 p^{23}+254912306189186884955406336 p^{22}+156626149291626983686483968 p^{21}+88404250727492514940483584 p^{20}+45878473655994873388013568 p^{19}+21899549954212600640726016 p^{18}+9613687988920313270974464 p^{17}+3878674960845100037209344 p^{16}+1436440532610345424093440 p^{15}+487439383606685797845888 p^{14}+151188354263541708202752 p^{13}+42726175153333960069440 p^{12}+10956635290090707948864 p^{11}+2536442727280948869408 p^{10}+526614895020854794464 p^9+97240367701683038832 p^8+15797199259738405344 p^7+2225820504393239016 p^6+266802755726152344 p^5+26481154011377592 p^4+2091275042562968 p^3+123287905489344 p^2+4826064408196 p+94133971181\right)^2}.\]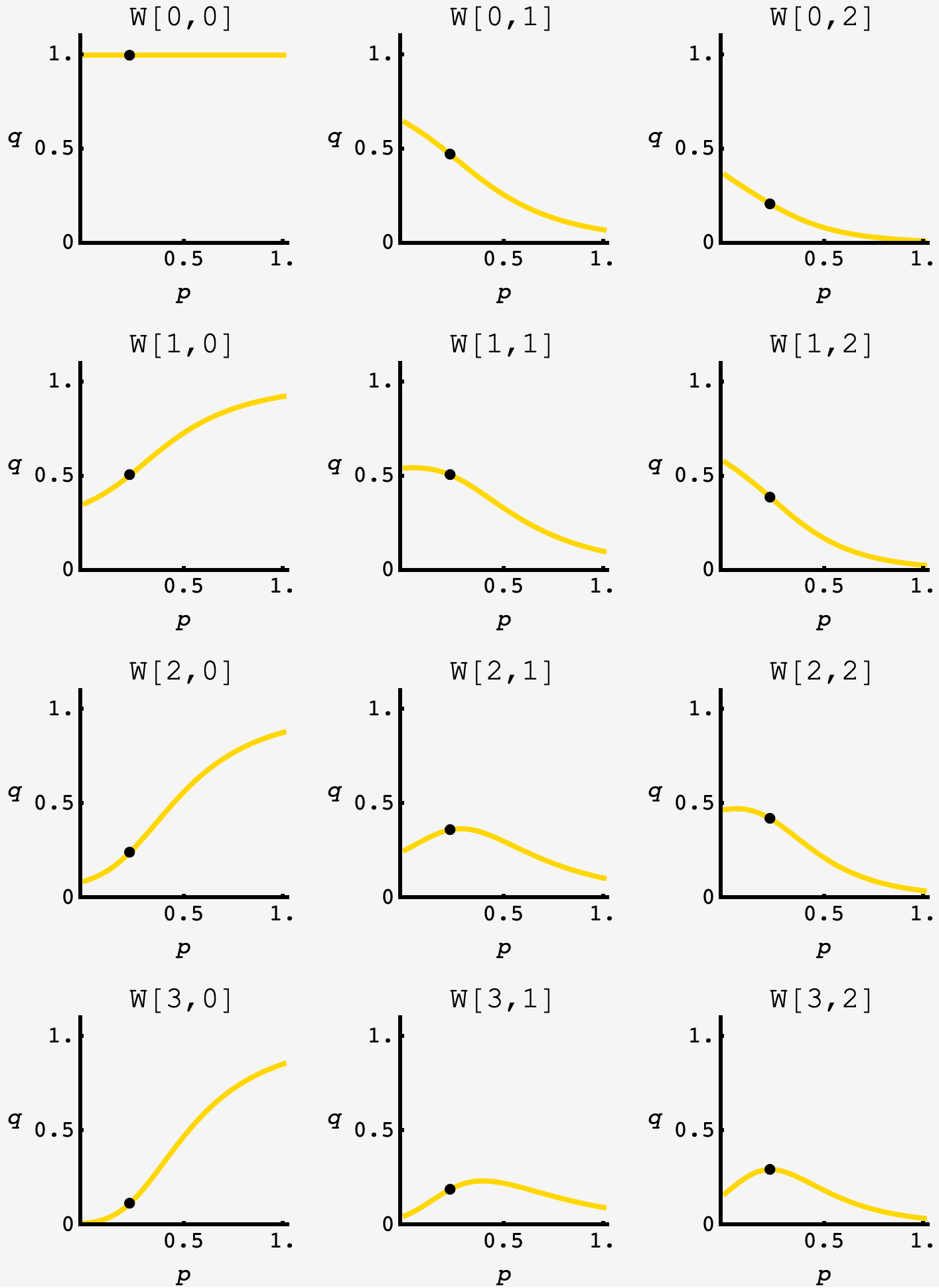
now, the players will adjust to any value of $p$ according to the decision rules above in order to pursue their own optimal outcomes. it’s only the league office that cares about full counts and can set $p$. plotting $W(3,2)$ (bottom right corner of diagram) we see the optimum is around $p \approx 22\%,$ indicated by the black dot in each plot. binary searching for the maximum, we find that full counts will happen in a fraction $q_\text{opt} \approx 0.295967993374272054854169869096$ of all at bats given that the league sets $p_\text{opt} \approx 0.226973232538510017721759332456$