Question: You’re playing a game of “high-low,” which proceeds as follows:
First, you are presented with a random number, $x_1$, which is between $0$ and $1$.
A new number, $x_2$, is about to be randomly selected between $0$ and $1$, independent of the first number. But before it’s selected, you must guess how $x_2$ will compare to $x_1.$ If you think $x_2$ will be greater than x1 you guess “high.” If you think $x_2$ will be less than $x_1,$ you guess “low.” If you guess correctly, you earn a point and advance to the next round. Otherwise, the game is over.
If you correctly guessed how $x_2$ compared to $x_1$ then another random number, $x_3,$ will be selected between $0$ and $1.$ This time, you must compare $x_3$ to $x_2,$ guessing whether it will be “high” or “low.” If you guess correctly, you earn a point and advance to the next round. Otherwise, the game is over.
You continue playing as many rounds as you can, as long as you keep guessing correctly.
You quickly realize that the best strategy is to guess “high” whenever the previous number is less than $0.5,$ and “low” whenever the previous number is greater than $0.5.$
With this strategy, what is the probability you will earn at least two points? That is, what are your chances of correctly comparing $x_2$ to $x_1$ and then also correctly comparing $x_3$ to $x_2$?
Extra credit: Your friend is playing an epic game of “high-low” and has made it incredibly far, having racked up a huge number of points.
Given this information, and only this information, what is the probability that your friend wins the next round of the game?
Solution
Assume $x_1$ is high, causing us to bet low. We’ll win if $x_2$ comes out less than $x_1.$ $x_2$ can end up high or low so we have two cases, either
- it’s low, and the chance to win with $x_3$ is $(1-x_2),$ or
- it’s high, and the chance to win with $x_3$ is $x_2.$
So, the conditional chance to win the second round is $\max(x_2, 1-x_2).$
To find the chance of winning, we allow for all possible values of $x_1$ and $x_2,$
\[\begin{align} \frac12P(\text{win}) &= \int\limits_{\frac12}^1\text{d}x_1\,\int\limits_0^{x_1}\text{d}x_2\,\max(x_2,1-x_2) \\ &= \int\limits_{\frac12}^1\text{d}x_1\,\left[ \int\limits_0^{\frac12}\text{d}x_2\, (1-x_2) + \int\limits_{\frac12}^{x_1}\text{d}x_2\,x_2\,\right]\\ &= \int\limits_{\frac12}^1\text{d}x_1\,\left[ \left(\frac12-\frac18\right) + \frac12\left(x_1^2-\frac14\right)\right] \\ &= \int\limits_{\frac12}^1\text{d}x_1\, \frac12x_1^2 + \frac14 \\ &= \frac{13}{48} \end{align}\]So the chance to win both rounds is $13/24$ or $\approx 54.2\%.$ The chance to win the first round alone is $3/4,$ so the conditional chance to win the second round is
\[\begin{align} P(\text{win second round|win first round}) &= 4/3\times13/24 \\ &= 13/18 \\ &\approx 72.2\%.\end{align}\]Extra credit
In the steady state, the distribution of winners should be stable from one round to the next (reminiscient of the tug of war problem).
Before we get into it, let’s think about the intuition. Suppose we’re currently at a low number. We can arrive here by coming from the low side or the high side. If it’s from the high side, then any place on that side could have been the previous bet. By contrast, if the last number was low, it could have only been to our left. So, the closer we are to the middle, the more potential places we could have come from, the more likely our current position, peaking at the middle. So, somewhat counterintutively, we should expect winning bets to be in the middle.
Let $\gamma(x)$ be the distribution of bets that end up winning, $y$ the winning bet at round $n,$ and $x$ the winning bet in round $(n+1)$. The probability that the winning bet has value $x$ is the probability that the last winning bet had value $y$ and $x$ was a valid bet from it.
If the last value was high (above $1/2$) then the jump distribution is uniform $1/y$ from zero to $y$, and if it was low (below $1/2$) then it’the jump distribution is uniform $1/(1-y)$ from $y$ to $1$.
Without loss of generality, let’s assume $x$ is low, then
\[\gamma(x) = \overbrace{\int\limits_{1/2}^{1} \text{d}y \frac{1}{y}\gamma(y)}^\text{coming from above 1/2} + \overbrace{\int\limits_0^{x} \text{d}y \frac{1}{1-y}\gamma(y)}^\text{coming from below $x$}.\]Taking the derivative we get
\[\frac{\text{d}\gamma(x)}{\text{d}x} = \frac{\gamma(x)}{1-x},\]Swapping the $\text{d}x$ and $\gamma(x)$ and integrating, we get $\log\,\gamma(x) = -\log(1-x) + \text{const.}$ which means $\gamma(x)$ is proportional to $1/(1-x)$ on the low side. On the high side, we can replace $(1-x)$ with $x,$ so the distribution there is proportional to $1/x.$ Each side has total probability $1/2$ but integrates to $\log 2$ so the normalization constant is ${1/(2\log 2).}$
We can write this as
\[\gamma(x) = \frac1{2\log2}\frac{1}{\max(x,1-x)}.\]In agreement with our reasoning from before, this shows that winning numbers cluster about the center despite providing less of an advantage.
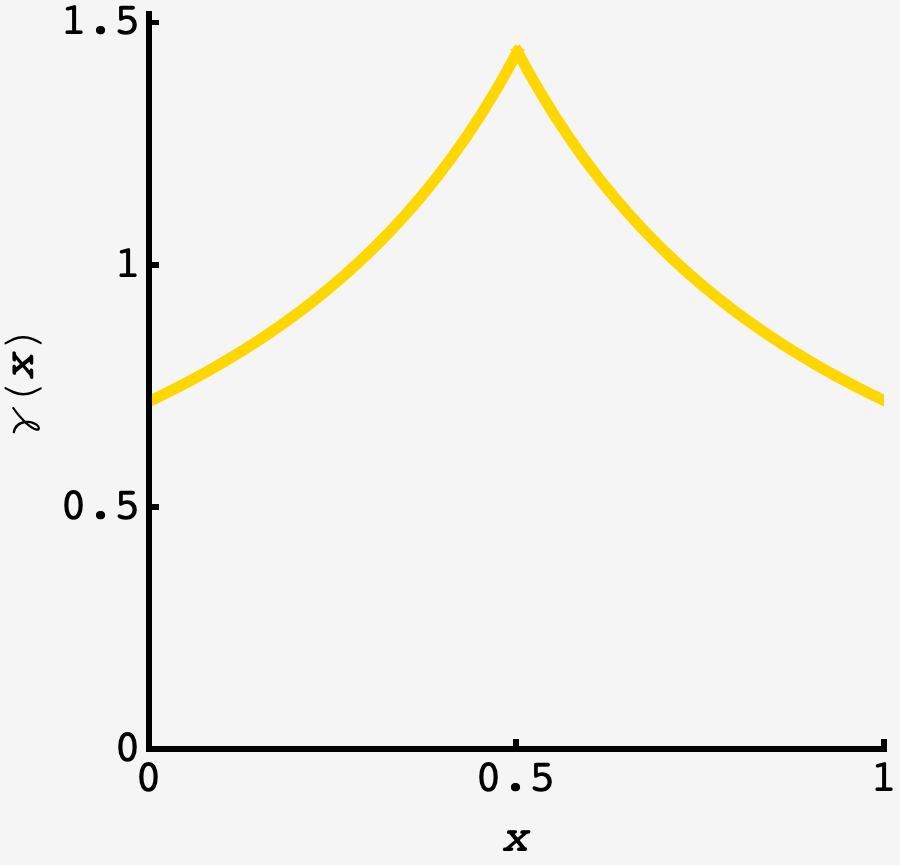
So what’s the chance to win a round in steady state? As before, chance to win given the last winning number $x$ is $\max(x,1-x)$ so the expected chance to win is
\[\begin{align} P(\text{win}) &= \int\limits_0^1\text{d}x\, \max(x,1-x) \gamma(x) \\ &= \frac{1}{2\log2}\int\limits_0^1\text{d}x\, \\ &= \frac{1}{2\log2} \\ &\approx 0.7213475204\ldots \end{align}\]This is remarkably close to the answer from before, indicating that the game is basically in steady state after just two rounds of play.