Question: Robot cars have a top speed (which they prefer to maintain at all times while driving) that’s a real number randomly drawn uniformly between $1$ and $2$ miles per minute. A two-lane highway for robot cars has a fast lane (with minimum speed $a$) and a slow lane (with maximum speed $a$). When a faster car overtakes a slower car in the same lane, the slower car is required to decelerate to either change lanes (if both cars start in the fast lane) or stop on the shoulder (if both cars start in the slow lane). Robot cars decelerate and accelerate at a constant rate of $1$ mile per minute per minute, timed so the faster, overtaking car doesn’t have to change speed at all, and passing happens instantaneously. If cars rarely meet (so you never have to consider a car meeting more than one other car on its trip, see Mathematical clarification below), and you want to minimize the miles not driven due to passing, what should $a$ be set to, in miles per minute? Give your answer to $10$ decimal places.
Example car interactions: suppose $a$ is set to $1.2$ miles per minute. If a car with top speed $1.8$ overtakes a car with top speed $1.1,$ neither has to slow down because they are in different lanes. If instead the car with top speed $1.8$ overtakes one with top speed $1.7,$ the slower car computes the optimal time to start decelerating for $30$ seconds (to reach $1.2$ miles per minute to switch to the other lane) so the faster car instantly passes and the slower car can immediately start accelerating for another 30 seconds to return to $1.7$ miles per minute. This pass cost $0.25$ miles (how far behind where the slower car would be if it continued at $1.7$ miles per minute).
If a car with top speed $1.1$ overtakes one with top speed $1.0$ in the slow lane, the slower (slowest!) car must decelerate for a full minute all the way to $0$ to allow the pass, and then accelerate for a full minute to reestablish its speed, losing exactly $1$ mile of distance.
Assume all car trips are of constant length $N,$ starting at arbitrary points and times along an infinitely long highway. This is made more mathematically precise below.
Mathematical clarification: Say car trips arrive at a rate of $z$ car trip beginnings per mile per minute, uniformly across the infinite highway (cars enter and exit their trips at their preferred speed due to on/off ramps), and car trips have a constant length of $N$ miles. Define $f(z,N)$ to be the value of a that minimizes the expected lost distance per car trip due to passing. Find $\lim\limits_{N\rightarrow\infty}\lim\limits_{z\rightarrow 0+}f(z,N).$
Solution
Because each car is spawned uniformly in time and space, we can condition on the two speeds $v_A$ and $v_B$ and find the relative probability of collision as the relative fraction of spawn times and distances that lead to intersection.
Relative probability of interaction
Let $t_B$ and $x_B$ be the time and position at which car $B$ was spawned, and $v_B$ be its speed. Considering the time and position of car $A$’s spawn to be $(0,0)$, we have
\[v_At_A = x_B + v_B\left(t_A-t_B\right).\]The latest spawn time that car $B$ can spawn is $0$, the time at which car $A$ comes off the highway, and the earliest it can spawn is one lifetime before car $A$ despawns, $-\mathcal{T}_B = -N/v_B$ so the range for $t_B$ is $\Delta t_B = \mathcal{T}_B = N/v_B.$
Because $t_B$ ranges from $-\mathcal{T}_B$ to $0,$ the range for $x_B$ is
\[0 \leq x_B \leq N - v_B \mathcal{T}_A,\]so $\Delta x_B = N(1-v_B/v_A).$
At the upper end, car $B$ spawns exactly where $A$ despawns and at the lower end, it is positioned so that $A$ can overtake it at the last minute.
Because we’re told that each car has at most one interaction, the probability that any given car of speed $v_A$ overtakes any given car of speed $v_B$ is proportional to the sub-volume of the $x_B, t_B$ coordinate space that leads to collision.
Since $\Delta t_B$ and $\Delta v_B$ are both simple expressions in terms of the velocities and $N$, they form a rectangle and the relative probability is
\[\begin{align} P(v_A\text{ overtakes }v_B) &\propto \Delta t_B\Delta x_B \\ &= N^2\left(1/v_B - 1/v_A\right) \\ &= N^2\frac{v_B - v_A}{v_Av_B} \end{align}\]Distance lost
With this in hand, we can find the relative expected lost distance, if only we had expressions for lost distance.
It is a bit awkward to frame the problem in terms of lost distance, since every trip lasts for $N$ miles. What’s actually lost is time. But alas.
The time spent decelerating at $1$ mile per minute per minute is twice the speed change over the acceleration, $2(v_B - a)/1.$ The distance lost accelerating and decelerating in the fast lane is the difference between the distance the slow car would have traveled in that time, $v_B\Delta t = 2v_B(v_B-a),$ and the distance it travels while decelerating, $\langle v\rangle \Delta t = \left(v_B + a\right)\left(v_B-a\right),$ which is
\[\begin{align} \left(v_B - \langle v\rangle\right)\Delta t &= 2v_B(v_B-a) - \left(v_B + a\right)\left(v_B-a\right) \\ &= 2v_B^2-2v_Ba - v_B^2 + a^2 \\ &= v_B^2 + a^2 - 2v_Ba \\ &= (v_B-a)^2. \end{align}\]In the slow lane, the car goes down to and up from zero ($a=0$) so it’s just $v_B^2.$
Expected loss
Now we can find the expected distance lost, with the help of computer algebra
\[\begin{align}\langle \text{distance lost} \rvert a \rangle &\sim \int \text{d}v_A \int\text{d}v_B\, P(v_A\text{ overtakes }v_B) \times \text{distance lost}(v_B) \\ &= \int\limits_1^a \text{d}v_A \int\limits_1^{v_A}\text{d}v_B\, v_B^2 \frac{v_A - v_B}{v_Av_B} + \int\limits_a^2 \text{d}v_A\, \int\limits_a^{v_A}\text{d}v_B \left(v_B-a\right)^2 \frac{v_A - v_B}{v_Av_B}\\ &= \frac{6 a^3 \log \left(\frac{2}{a}\right)+\left(6-36 a^2\right) \log (a)+9 a (2 a (a-1+\log (4))-5)+16}{18 (\log (8)-2)},\end{align}\]which matches an $N=10^6$-trial simulation pretty well
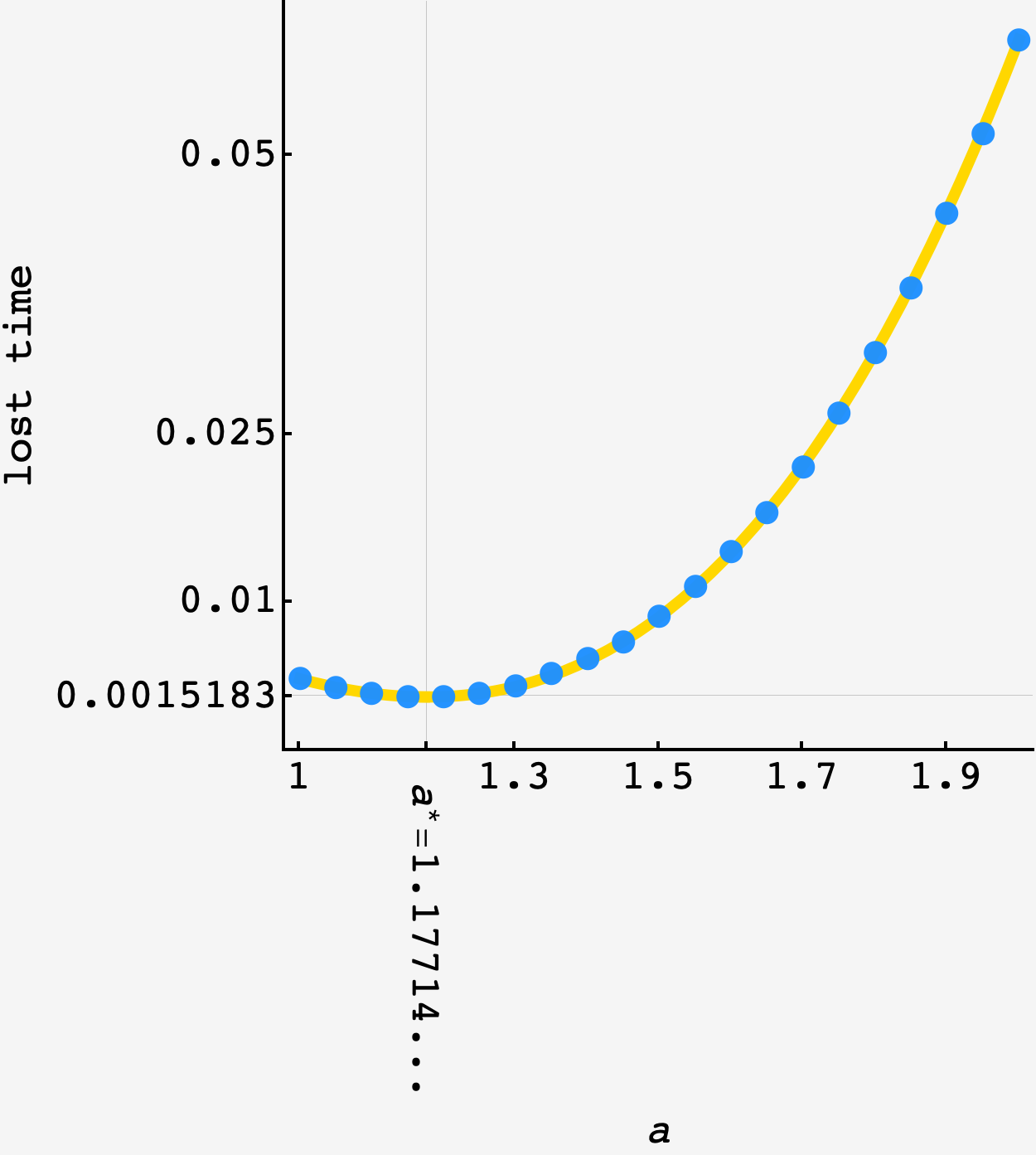
Minimizing the result with respect to $a$ we get $a^* \approx 1.1771414167566419952\ldots$