Can you weave the web?

Question: A spider weaves a web within a unit square (i.e., a square with side length $1$) in the following haphazard manner:

First, the spider picks two points at random inside the square. In particular, it picks the points “uniformly,” meaning any point is equally likely to be picked as any other point. Next, the spider connects the two points with a strand of silk and extends the strand to two sides of the square.

Within the unit square, which point (or points) is most likely to be on a new strand of silk, whose two defining points have not yet been picked?

Extra Credit: as we just acknowledged, there exists a point (or points) in the unit square that is more likely than any others to be on the randomly selected silk strand.

At the same time, there exists a point (or points) in the unit square that is less likely than any others to be on the random strand.

How much more likely is a most likely point to be on the strand than a least likely point? More specifically, suppose the maximum of the probability density for being on the strand is $p_\text{max}$ and the minimum probability density is $p_\text{max}.$ What is the ratio $p_\text{max}/p_\text{max}$?

(Fiddler on the Proof)

Solution

First, let’s get some intuition for the problem.

Intuition

The probability that two random points fall on a particular line through a point $\mathbf{p}$ is bigger the longer that line is. In particular, it is proportional to the number of ways to pick two points from that line, which is proportional to the square of its length. Already, we can say the center of the square will have the greatest chance to fall on a random line, since on average, the lines through it are most numerous and longest.

Another point of interest is any corner of the square. For argument’s sake, let’s consider the lower left corner. While the lines that go through it range from one side length up to $\sqrt{2}\approx 1.414,$ a line must have positive slope to qualify, meaning a half of all lines are ineligible. We should expect the corners to have pretty low probability.

A final point of interest is the middle of any edge. The length of lines through these points range from half a side length, to just over a side length. These should also have low probability, but it’s hard to compare with corner points without more work.

Simulation

We can confirm these intuitions by measuring the probability that any given point in the unit square is hit by a random line. We do this by discretizing the unit square into $10^{-3} \times 10^{-3}$ unit cells, picking two random points, establishing the line through them, and measuring which unit cells are touched by it. Doing this for ${N=4\times10^6}$ random lines in the unit square, we get the following heatmap:

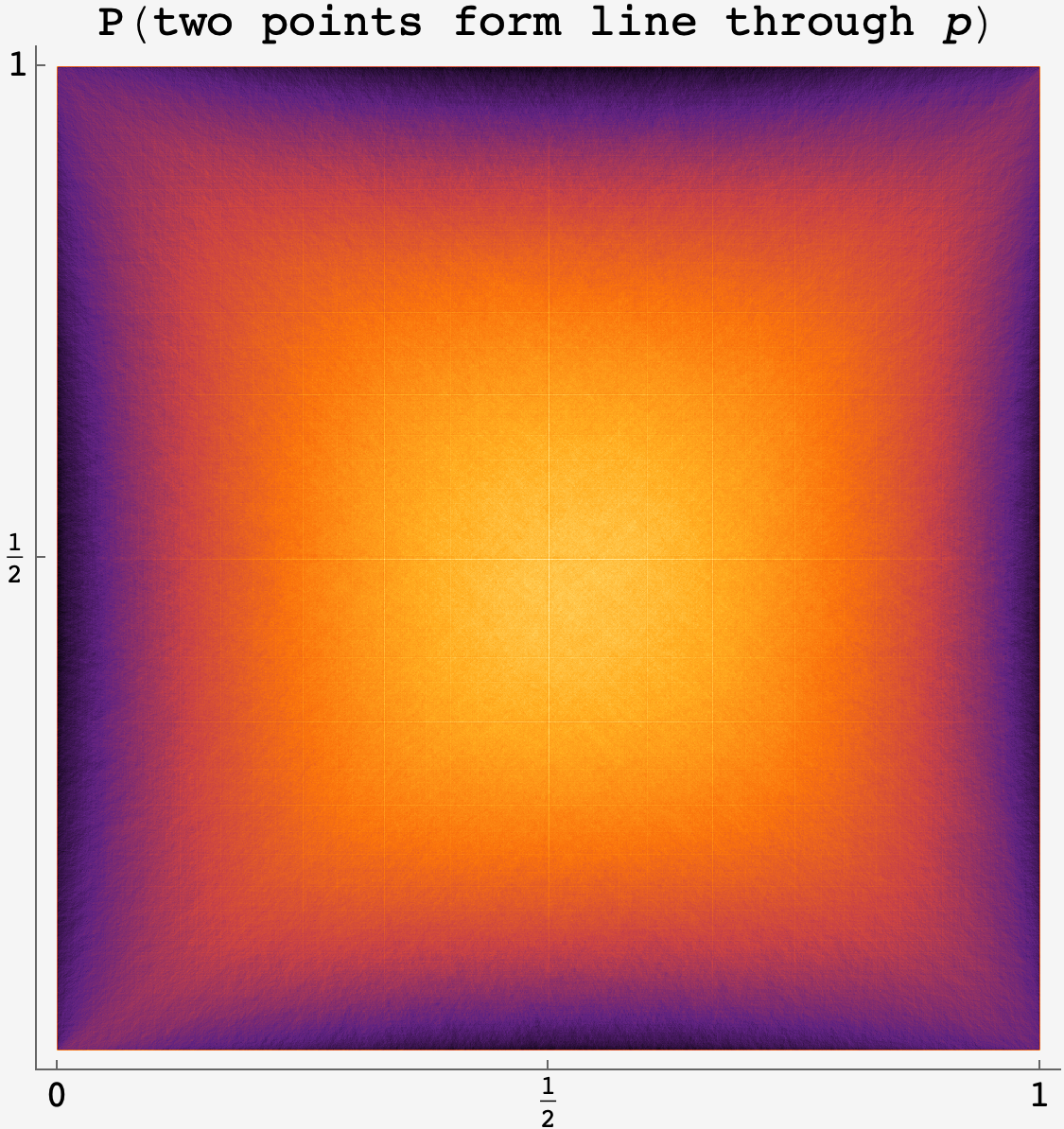
It seems like the center has the greatest probability, and the middle-edge position is slightly lower than the corners, while both are much lower than the center.

Calculation

The probability density that the two random points $x$ and $y$ form a line through a given point $p$ is proportional to

As literal as it seems, we can work this out to get the probability density for any $\mathbf{p}.$ Concretely, let’s work out the case where $\mathbf{p}$ is the lower left corner. We start by carrying out the integral over $\mathbf{y}:$

The indicator function is $1$ for all points $\mathbf{y}$ that fall on a line through the lower left corner and $\mathbf{x}.$ Drawing this out for an arbitrary $\mathbf{x}$, the support is the line labeled $\ell(\theta).$

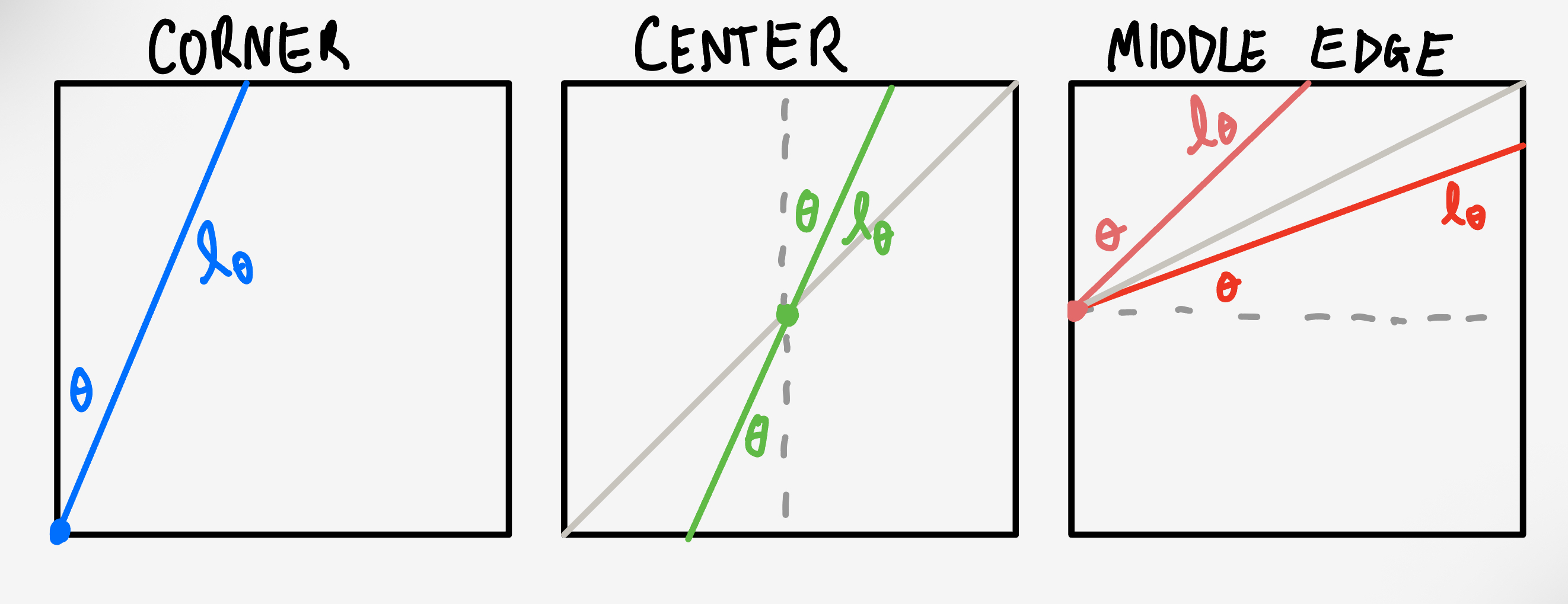
Now we just have to integrate over $\mathbf{x}.$ To do this, let’s represent $\mathbf{x}$ in polar coordinates $\mathbf{x} = (r, \theta),$ changing $\text{d}\mathbf{x}$ to $r\, \text{d}r\, \text{d}\theta.$ With this change, the integral becomes

The range for $\theta$ is just zero to $\pi/4$ while $r$ ranges from zero to $\ell(\theta),$ so the integral further simplifies to

This has two intuitive interpretations:

• for a given choice of $\mathbf{x},$ the probability that $\mathbf{y}$ falls on the line from $\mathbf{x}$ to $\mathbf{p}$ is proportional to the length of that line $\ell(\theta).$ Next, the area of the polar strip at angle $\theta$ from which we can pick $\mathbf{x}$ is $\frac12 \ell^2(\theta)\,\text{d}\theta.$
• we can index the lines by their angle. The probability that two random points fall on a line through $\mathbf{p}$ at a given angle $\theta$ is proportional to the number of pairs of points that can define such a line which is the handshake between all points on the line, yielding a factor of $\frac12 \ell^2(\theta).$ Next, the probability that a random line through $\mathbf{p}$ would have angle $\theta$ is proportional to the number of ways to choose a point at an angle $\theta$ to $\mathbf{p},$ which is proportional to $\ell(\theta).$

The interpretive confusion comes from $\ell$ doing double duty in the probability and in the measure of the physical space the points are chosen from.

Returning to the calculation, we need to find a concrete expression for $\ell(\theta).$ From the picture, it has a constant vertical component of $1$ while its horizontal component is $\ell(\theta)\sin\theta.$ This means its length is given by

which leads to $\ell(\theta) = 1 / \cos\theta.$ So, the probability density for a corner of the square is proportional to

The case for the center is nearly the same, except that the green angle ranges from $-\pi/4$ to $\pi/4$, doubling the result so that $P_\text{center} = 2P_\text{corner} \approx 2.29559.$

The middle edge is slightly more complicated, breaking into two distinct integrals. The first, given by the salmon colored line in the diagram, has constant vertical component $\frac12$ and horizontal component $\ell_\theta \sin(\theta).$ This means that $\ell_\theta^2 = 1/2^2 + \sin^2\theta \ell_\theta^2$ which leads to $\ell_\theta = \frac1{2\cos\theta}.$ The salmon angle starts at zero and ranges up until $\tan\theta = 1/(1/2)$ or $\theta = \arctan 2.$ The second, given by the red line in the diagram, has constant horizontal component $1$ and vertical component $\ell_\theta \sin\theta$ which, like the corner and center cases, leads to $\ell_\theta = 1/\cos\theta.$ The red angle starts at zero and ranges up to $\tan\theta = 1/2$ or $\theta = \arctan \frac12.$

Adding the two pieces, we get

This shows that $P_\text{center}/P_\text{middle-edge}$ is, after simplifying:

We can estimate these quantities by generating random lines, discretizing the square, and testing if each line passes within a unit cell of $\mathbf{p}$

import random
import math
import pandas as pd

eps=1e-3

def estimate_density(p, N=400_000_000):
    # MC estimate using small-band approximation.
    # pdf ~= P(distance(line(x, y), p) < eps ) / eps

    px, py = p
    count = 0
    for _ in range(N):
        x1, y1 = random.random(), random.random()
        x2, y2 = random.random(), random.random()
        dx, dy = x2 - x1, y2 - y1
        len_sq = dx * dx + dy * dy
        dist = abs(dx * (y1 - py) - dy * (x1 - px)) / math.sqrt(len_sq)
        if dist < eps:
            count += 1
    return count / (N * eps)

test_points = {
    # put zero just off the boundary to avoid edge effects
    "center"      : (0.5, 0.5),
    "middle edge"   : (0.5, 0.001), 
    "corner": (0.001, 0.001)
}

results = []
for label, p in test_points.items():
    f_est = estimate_density(p)
    results.append({"Point": label, "Estimated pdf(p)": round(f_est, 3)})

df = pd.DataFrame(results)

which leads to the following estimates at $N=4\times 10^8:$

Taking ratios, we see that $P_\text{center}/P_\text{middle edge} \approx 2.560,$ in precise agreement with the calculation.

General integral

We can generalize the expression for $\ell(\theta)$ for any interior point $\mathbf{p} = (a,b)$ in the square as the sum of the distances to the wall at the given $\theta$

Integrating over all angles as above, we find the relative density:

We can use this to evaluate the relative probability density for any two points in the square. For example, $P\left(\tfrac{2}{10},\tfrac{3}{10}\right)/P\left(\tfrac{1}{2},\tfrac{1}{2}\right)$ is equal to

or, as any good pocket calculator will show, roughly $0.7349890315253553.$