Question: Fiddlish is written using a monospace font, meaning each character (including spaces) takes up the same amount of horizontal space. As before, lines of text are very, very long, and each next word has a $50$ percent chance of being three letters and a $50$ percent chance of being four letters. Each line begins with a new word (i.e., words at the end of a line are not hyphenated into the next line).
Suppose the $12^\text{th}$ character of a specific line of text is a space. You want to know how long the river down and to the right from this space will be. For example, suppose the $13^\text{th}$ character on the next line and the $14^\text{th}$ character on the line after that are both spaces, but the $15^\text{th}$ character on the very next line is not a space. In this case, the river would have a length of $3.$ (By this definition, the length of the river is always at least $1.$)
On average, how long do you expect the resulting river from the given space (again, the $12^\text{th}$ character in its line) to be?
Solution
After a long stretch of words, correlations with the beginning of the line decay and we should be equally likely to hit a space at any position.
Since half the words are three letters and half are four, this means that two out of every nine characters is a space, and $\lim\limits_{\ell\rightarrow \infty} P_\text{space}(\ell) \rightarrow 2/9.$
Since a new word starts each line, we are asking what is the probability that the $13^\text{th}$ character on a new line is a space, and the $14^\text{th}$ character on the next line is a space, and so on until line $\ell$ at which it ends, where we multiply by the probability that the $(12+j)^\text{th}$ character on that line is a letter. In other words
\[\begin{align} P_\text{river}(\ell) &= P_\text{space}(12+1)\cdot P_\text{space}(12+2) \cdots P_\text{space}(12+\ell-1)\cdot\left(1-P_\text{space}(12+\ell)\right) \\ &= \left(1-P_\text{space}(12+\ell)\right)\prod\limits_{j=1}^{\ell-1} P_\text{space}(12+j) \end{align}\]Because every word begins after a space and ends on a space, the probability that position $j$ is a space is the probability that position $(j-4)$ ended on a space and the next word had three letters plus the probability $(j-5)$ ended on a space and the next word had four letters. Since the probability of a three or four letter word after a space is $\frac12$, this becomes
\[P_\text{space}(j) = \frac12 P_\text{space}(j-4) +\frac12 P_\text{space}(j-5).\]At this point, we could code the recursion to find $P_\text{space}(j)$ and then take the weighted sum
\[\langle \ell\rangle = \dfrac{\sum\limits_{\ell=1}^\infty \ell P_\text{river}(\ell)}{\sum\limits_{\ell=1}^\infty P_\text{river}(\ell)}.\]But we can make some more progress analytically, turning to the glory of generating functions. The idea is to make a polynomial where the coefficient on $z^\ell$ represents the probability to have a space at position $\ell$. In principle, we could make the quantity $\frac12(z^4 + z^5)$, raise it to a high enough power (anything bigger than $\ell/4$), expand it, and then count how many terms of $z^\ell$ result. With that motivation out of the way, we can accept that such a polynomial would be useful and find a way to do it more neatly.
The polynomial so described is
\[G(z) = \sum\limits_{\ell=1}^\infty P_\text{space}(\ell)z^\ell.\]Taking the recursive relationship, multiplying by $z^j$ and summing both sides, we get
\[\begin{align} P_\text{space}(j)z^j &= \frac12z^j P_\text{space}(j-4) + \frac12z^j P_\text{space}(j-5) \\ \sum\limits_{j=6}^\infty P_\text{space}(j)z^j &= \frac12z^4\sum\limits_{j=6} z^{j-4}P_\text{space}(j-4) + \frac12z^5\sum\limits_{j=6} z^{j-5}P_\text{space}(j-5) \\ G(z) - P_\text{space}(4)z^4 - P_\text{space}(5)z^5 &= \frac12 z^4 G(z) + \frac12 z^5 G(z) \\ G(z) &= \frac{z^4+z^5}{2-z^4-z^5} \end{align}\]To extract the probabilities, we need to turn this into an unambiguous series in $z$:
\[\begin{align} G(z) &= \frac12 \dfrac{(z^4+z^5)}{1-\frac{z^4+z^5}{2}} \\ &= \frac12 (z^4+z^5)\left(1 + \frac{z^4+z^5}{2} + \frac{(z^4+z^5)^2}{2^2} + \ldots \right) \\ &= \frac12 \sum\limits_{j=1} \frac{1}{2^{j-1}}(z^4+z^5)^j \\ &= \sum\limits_{j=1} \frac{z^{4j}}{2^j}(1+z)^j \end{align}\]To get a $z^\ell$ term we need the $4j$ from $z^{4j}$ plus the exponent of a term from the expansion of $(1+z)^j$ to equal $\ell,$ the coefficients of which are binomial coefficients. Putting it together, we get the sum
\[\begin{align} P_\text{space}(\ell) &= \left[z^\ell\right] \\ &= \sum\limits_j \dfrac{\dbinom{j}{\ell - 4j}}{2^j}. \end{align}\]This has a straightforward interpretation: $j$ is the number of words in a line, and each one contributes at least $4$ characters (four characters for three-letter words, and five for four-letter words). So, $(\ell - 4j)$ is the number of four letter (five character) words. When $j$ total words are used, and $(\ell-4j)$ of them are four letter words, there are $\binom{j}{\ell-4j}$ ways to order them. The sum takes care of all feasible word counts, and each particular choice of $j$ words has probability $1/2^j.$
For small values of $\ell$, $P_\text{space}(\ell)$ fluctuates but eventually settles down to $2/9:$
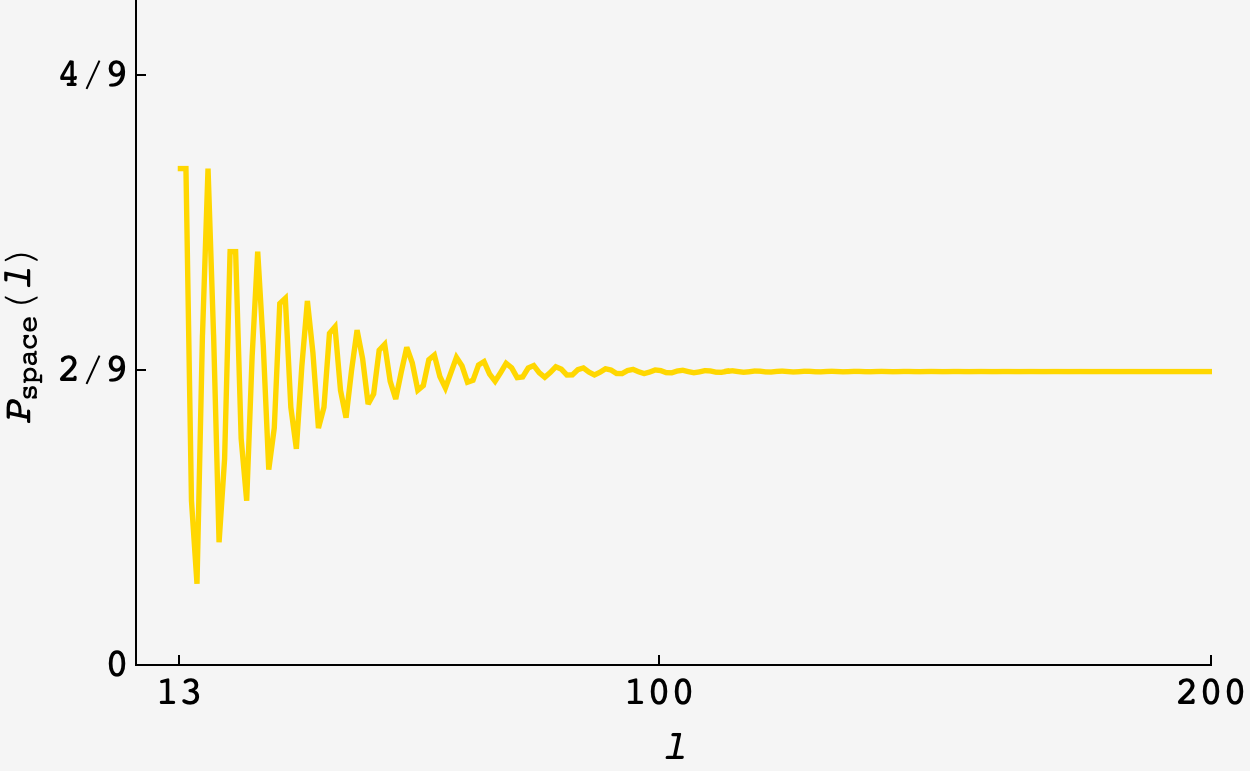
With this in hand, we can evaluate the weighted average which comes to $\langle \ell\rangle \approx 1.5347081153095188$
def P_space(l):
return 1/2 * sum(
math.comb(j, l - 4 * j) / 2 ** (j - 1)
for j in range(l // 5, l // 4 + 1)
)
def P_river(l):
P_return = 1
for i in range(1, l):
P_return *= P_space(12 + i)
return P_return * (1 - P(12 + l))
exp_l = sum(
j * P_river(j)
for j in range(1, 100)
) / sum(
P_river(j)
for j in range(1, 100)
)
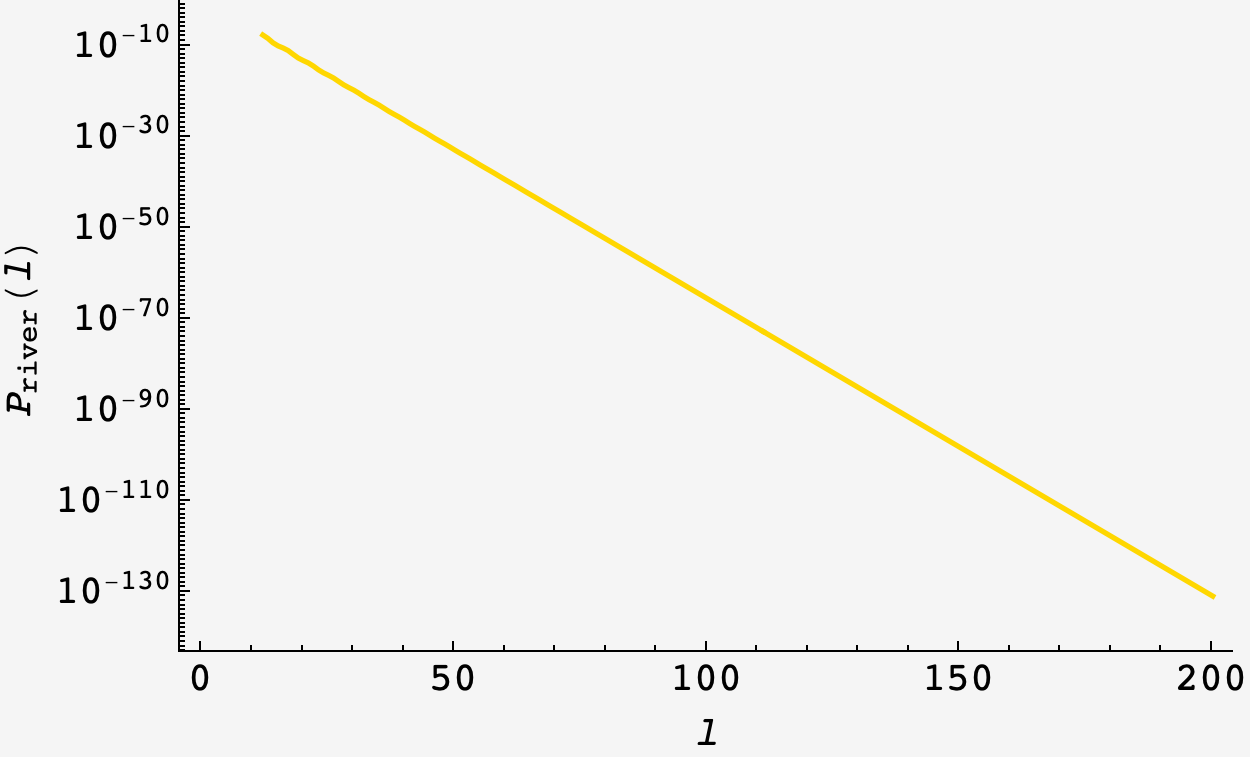
Looking at the log plot, this eventually falls as a power law (the straight line on the log plot means it’s proportional to $\ell^{-t}$; eying it up the slope is about $-125/200$ which is approximately $\log_{10}2/9$):
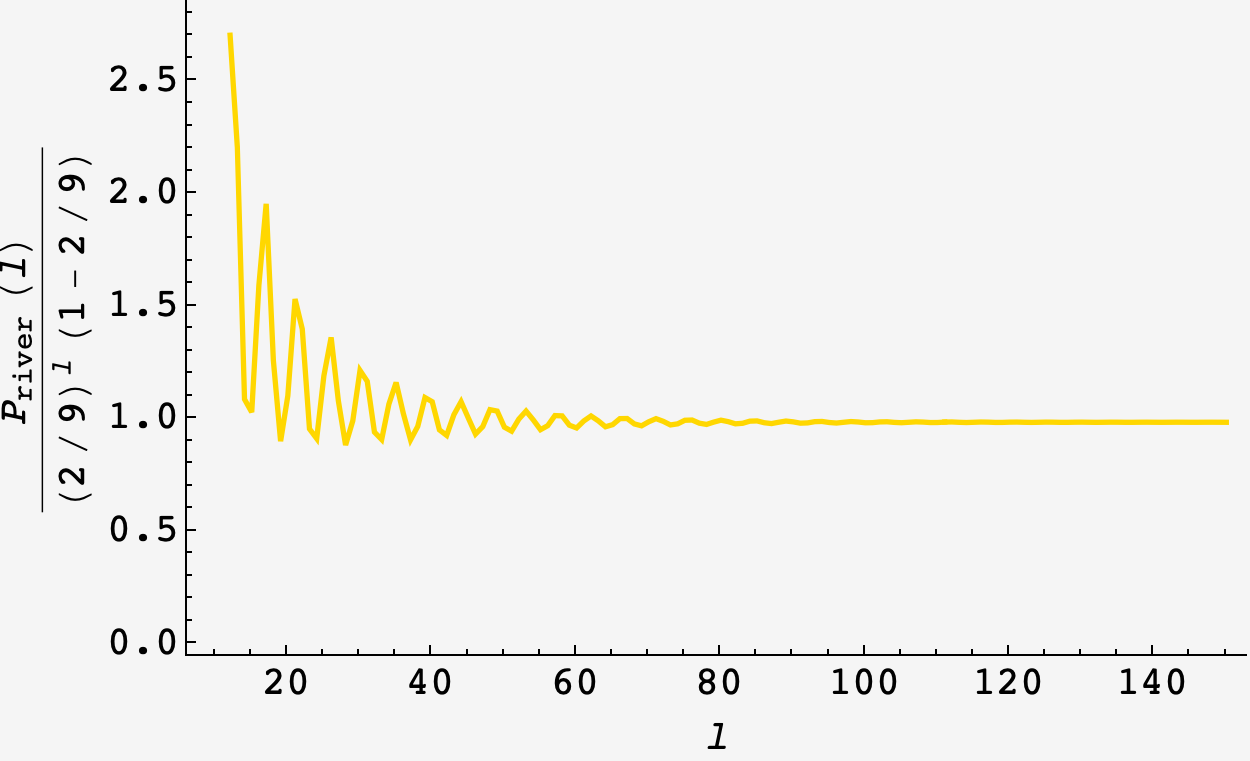
Interestingly, $P_\text{river}(\ell)$ settles very close to $(2/9)^\ell(1-2/9)$ which is the naive solution times an extra factor of $2/9.$