Question: For a fixed $p,$ independently label the nodes of an infinite complete binary tree $0$ with probability $p,$ and $1$ otherwise. For what $p$ is there exactly a $1/2$ probability that there exists an infinite path down the tree that sums to at most $1$ $($that is, all nodes visited, with the possible exception of one, will be labeled $0)?$
Solution
To access a path with at most one label placed, it either must be the case that:
- the current node is labelless and goes on to a path with at most one label placed, or
- the current node is labelled and goes on to a path with no labels placed.
Calling the probability of a zero-label path $P_\text{zero},$ and the probability of a path with at most one label $P_\text{zero or one},$ we can capture this with the following equation:
\[\begin{align} P_\text{zero or one} &= P(\text{zero or one}|\text{first node is zero})P(\text{first node is zero}) \\ & \,\,\, + P(\text{zero}|\text{first node is 1})P(\text{first node is 1}) \\ &= 2p P_\text{zero or one} + 2(1-p)P_\text{zero} - p P^2_\text{zero or one} - (1-p) P^2_\text{zero}. \end{align}\]We can find the probability of a zero-label path with the same kind of analysis:
\[P_\text{zero} = 2p P_\text{zero} - p P^2_\text{zero}.\]This is solved by
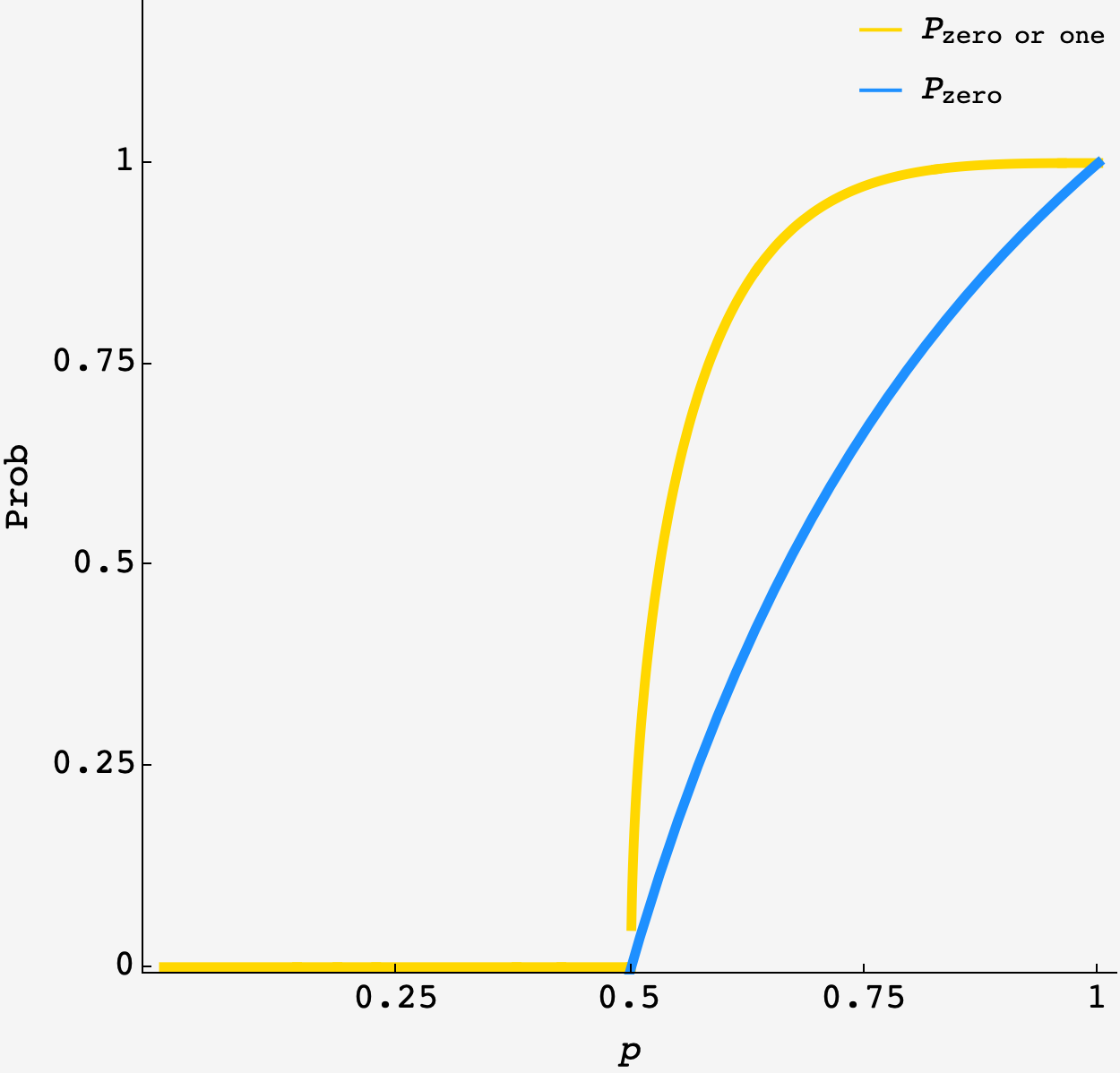
\[P_\text{zero} = \begin{cases} 0 & p < \frac12 \\ \dfrac{2p-1}{p} & p \geq \frac12 \end{cases}\]So, $P_\text{zero}$ is zero until $p=\frac12$ after which it shoots up, approaching $1$ as $p$ approaches $1.$ Plugging this solution into the first equation, we can solve it for $P_\text{zero or one}$:
\[P_\text{zero or one} = \dfrac{2 p+\sqrt{\dfrac{4 (p-1)^3}{p}+1}-1}{2 p}.\]Plugging in $P_\text{zero or one}=\frac12,$ we can solve for the value $p_\frac12$:
\[\begin{align} p_{1/2} &= \dfrac{1}{9} \left(10-\dfrac{4\ 2^{2/3}}{\sqrt[3]{9 \sqrt{57}-67}}+\sqrt[3]{2 \left(9 \sqrt{57}-67\right)}\right) \\ &\approx 0.5306035754 \end{align}\]Plotting $P_\text{zero or one}$ alongside $P_\text{zero},$ we see similar thresholding behavior with a much steeper rise after $p=\frac12$: