Question: you are planning a picnic on the remote tropical island of 𝜋-land. The island’s shape is a perfect semi-disk with two beaches: Semicircular Beach (along the northern semicircular edge of the disk) and Diametric Beach (along the southern diameter of the disk).
If you pick a random spot on 𝜋-land for your picnic, what is the probability that it will be closer to Diametric Beach than to Semicircular Beach?
Extra Credit: now suppose the island of $\pi$-land, as described above, has a radius of $1$ mile. That is, Diametric Beach has a length of $2$ miles.
Again, you are picking a random point on the island for a picnic. On average, what will be the expected shortest distance to shore?
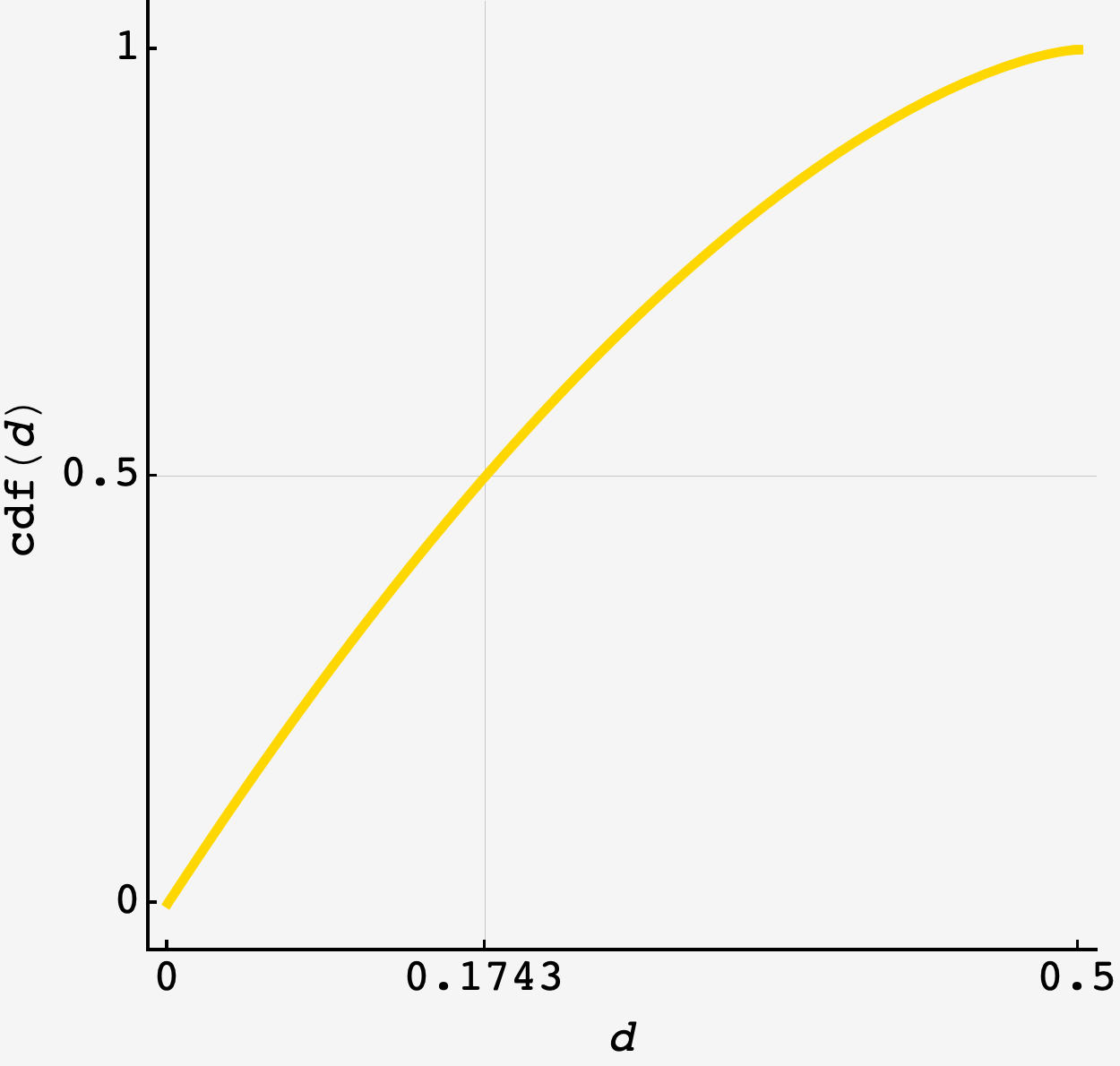
Extra Extra Credit: what is the median shortest distance to the shore?
Solution
At any position $(x,y)$ on the island, the distance to diametric beach (the southern diameter) is $y$ and the distance to semicircular beach is $1-\sqrt{x^2 + y^2}.$
There is a curve such that, on its northern side, semicircular beach is closer and, on its southern side, diametric beach is closer.
\[\begin{align} y &= 1 - \sqrt{x^2 + y^2} \\ (y-1)^2 &= x^2 + y^2 \\ 1 - 2y &= x^2 \\ y &= \frac12\left(1 - x^2\right) \end{align}\]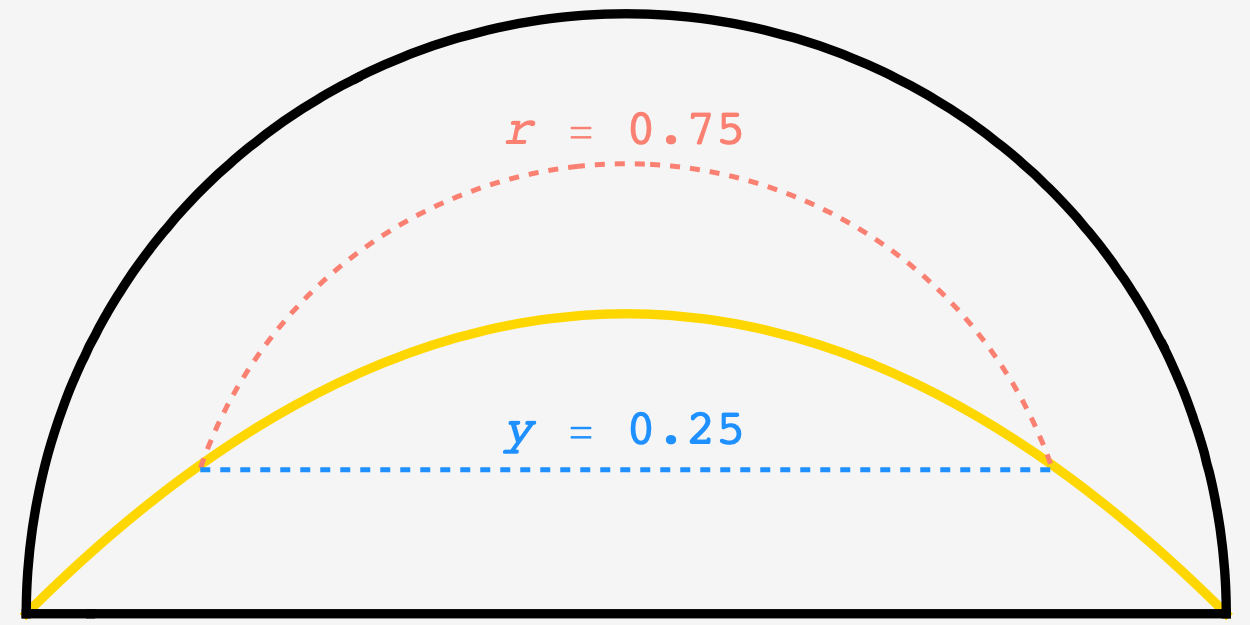
The probability that diametric beach is closer is just the area under this curve relative to the entire semicircle:
\[P(\text{diametric}) = \frac{2}{\pi}\int\limits_{-1}^1\text{d}x\, \frac12(1 - x^2) = \frac{4}{3\pi}.\]To find the average distance, we could find the average of $(1-r)$ in the upper region, of $y$ in the lower region, and take the weighted sum. Instead we’re going to get the probability density function of $r$ so that we can find the median, which is truer to the plight of the everyman, as beach outings go.
Probability density
In the diametric region, the probability that we’re $y^*$ away from the beach is proportional to the length of the horizontal strip between the points where the curve crosses $y=y^{*}$ (the blue dashed line in the diagram):
\[\begin{align} P(y) &\propto \sqrt{\frac12 - y} \\ &= 3\sqrt{2}\sqrt{\frac12 - y}. \end{align}\]In the semicircular region, the probability that we’re at radius $r$ (i.e. at distance $(1-r)$ from the beach) is proportional to the length of the circular arc between the points where the curve is $r$ away from the origin (the salmon dashed curve in the diagram).
This occurs when $r\sin\theta = 1 - r.$ Solving this for $\theta$ we get ${\theta(r) = \arcsin\frac{1-r}{r}}$ and
\[\begin{align} P(r) &\propto 2r\left(\pi/2-\theta(r)\right) \\ &\propto r\left(\pi - 2\arcsin\frac{1-r}{r}\right) \\ &= \frac{6}{3\pi-4}r\left(\pi-2\arcsin\frac{1-r}{r}\right). \end{align}\]We can turn these into a $\text{pdf}$ for the distance $d$ like so
\[\begin{align} P(d\,\text{away}) &= P(d\,\text{away}|\text{diametric})P(\text{diametric}) + P(d\,\text{away}|\text{semicircular})P(\text{semicircular}) \\ &= 3\sqrt{2}\sqrt{\frac12 - d}\frac{4}{3\pi} + \frac{6}{3\pi-4}(1-d)\left(\pi-2\arcsin\frac{d}{1-d}\right)\left(1-\frac{4}{3\pi}\right) \end{align}\]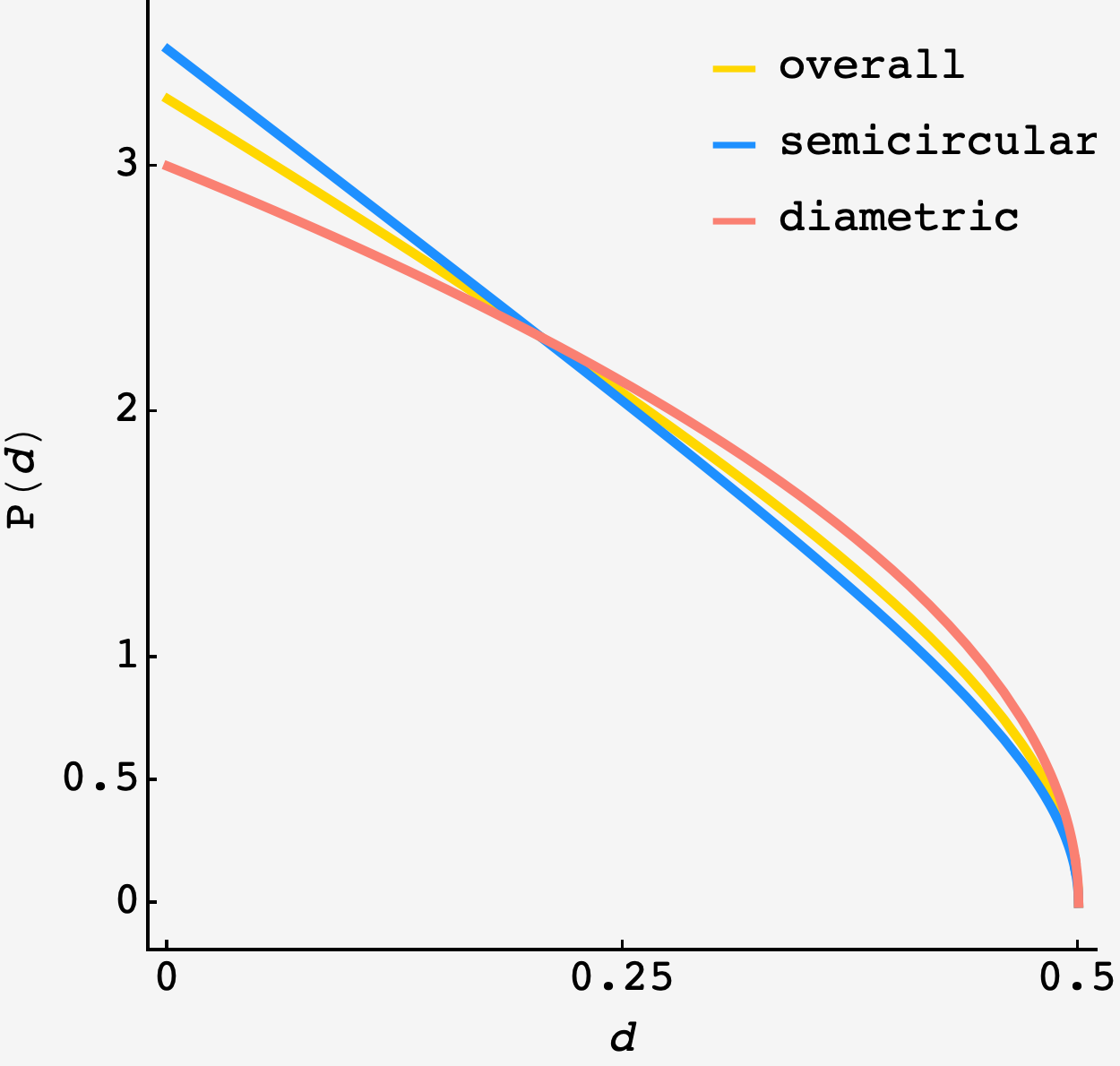
Plotting this, we see that the probability is highest for small distances, and goes to zero by $d = \frac12.$ In the semi-circular region, there is a bit more probability at the shore than in the diametric region. This makes sense because the boundary is relatively flat near diametric beach, while the boundary curves up towards the arcs of constant distance for semicircular beach.
With the $\text{pdf}$ in hand, we can find the expectation value by integration
\[\begin{align} \langle d\rangle &= \int\limits_0^{\frac12}\text{d}d\, d\, P(d) \\ &= \frac13 - \frac{4}{9\pi}\\ &= 0.1918622728. \end{align}\]We can also find the median by binary search. The $\text{cdf}$ of $P(d)$ is $\int\limits_0^d\text{d}d^\prime P(d^\prime)$ which equals $\frac12$ when $d\approx 0.1742619757.$