Question: My kids love Magna-Tiles. After some time playing around with them myself, I began to appreciate how they always seem to stick together, regardless of how they are rotated—a property I wouldn’t typically associate with magnets.
Every magnet has a north pole and a south pole. If you have two magnets and put their two north poles together, they repel. But rotate one of the magnets, and now you have a north pole near a south pole, so they’ll attract.
But Magna-Tiles are somehow impervious to rotation. Put one square tile on top of another and they stick together very well. Rotate one of the squares 90 degrees, they still stick. Flip one over, they still stick.
The tiles even stick together (though not as strongly) when placed side by side. Again, rotating or flipping a tile results in the same attraction.
Clearly, the eight magnets embedded along each square’s perimeter must be very cleverly oriented.
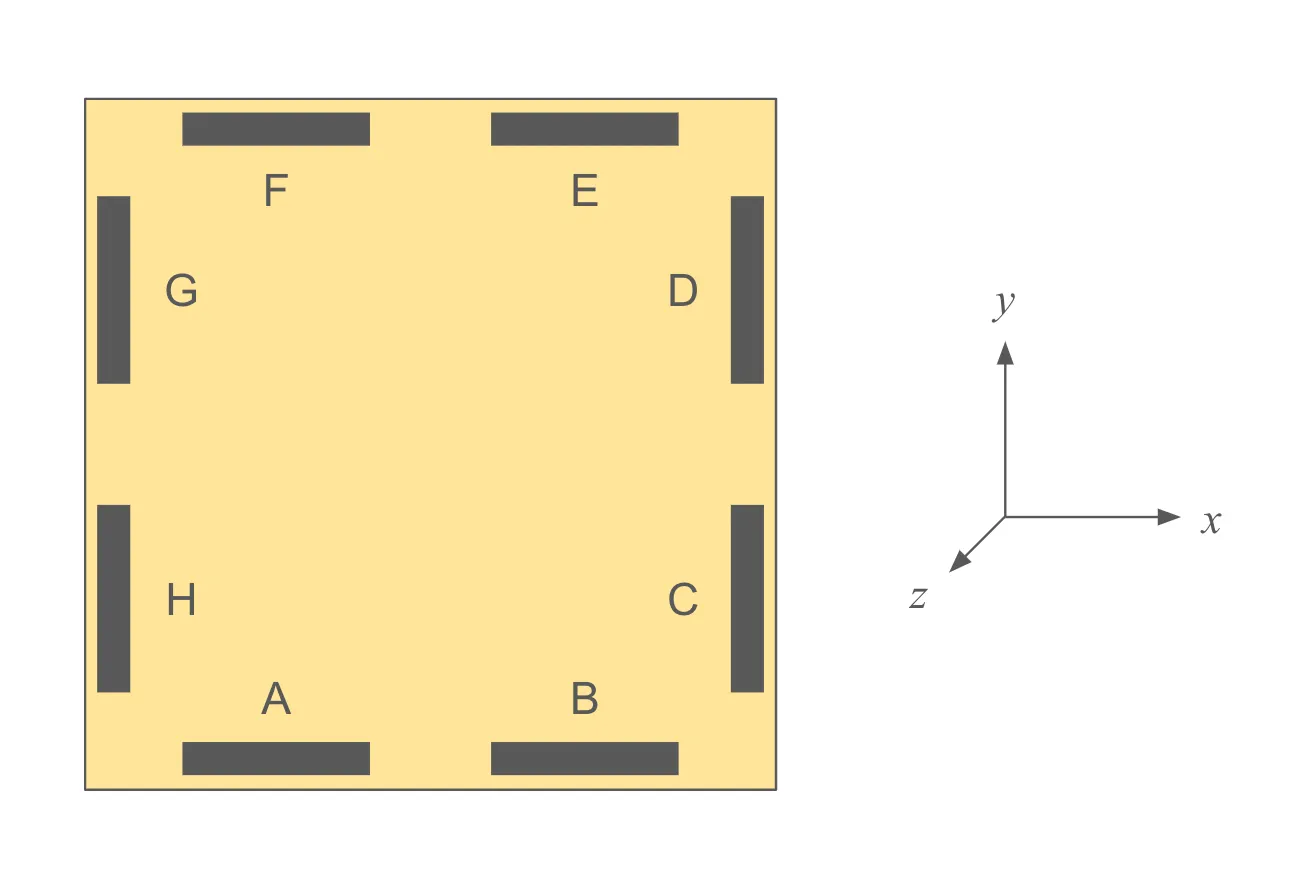
Consider the diagram below, which shows eight magnets along a square tile’s perimeter, labeled A through H in a counterclockwise manner. The tile lies in the $x-y$ plane, and the $z-$axis is coming out of the screen toward you.
Given the square tiles’ imperviousness to rotation, what must the orientation of these eight magnets be? For each tile, you should describe the direction from its south pole to its north pole. (More than one answer is possible here.)
Extra credit When you place one square Magna-Tile perfectly atop another, they stick together really well. Suppose each square has side length 1 unit and a thickness of $0.1$ units.
We can model each tile’s eight magnets as monopoles that are either “north” or “south.” (Yes, I know magnetic monopoles don’t exist, but they’re a sufficient approximation for the following puzzle.) Let’s also assume these monopoles are points, rather than bars. They lie on each edge, one- and three-quarters of the way from one end to the other.
Assume that the energy between any two magnetic monopoles is $q_1q_2/r$, where $r$ is the distance between them, and $q_i$ is $+1$ for “north” and $-1$ for “south.”
When one square lies in a plane directly above another (i.e., the planes are parallel and vertically separated by a distance of $0.1$), the lowest-energy arrangement is when the top square is directly above the bottom one. This arrangement is stable, meaning a slight translation or rotation of either square won’t lower the energy. You should assign north vs. south polarity to each monopole on the bottom square based on your work in this week’s Fiddler. The corresponding monopoles on the top square should have the opposite polarity, so that the two squares stick together. If you did this correctly, you should be able to confirm that this arrangement has a magnetic energy between the squares of approximately $-54.27$. (Note: This figure does not include any magnetic energy within a square.)
Your Extra Credit challenge is to determine the stable arrangement with the next-lowest energy. Again, you should assume that the monopoles from one square and the other are vertically separated by $0.1$, but that the squares are otherwise free to translate or rotate in their respective planes.
What is this next-best arrangement, and what is its corresponding magnetic energy between the squares?
(Hint: If you have any Magna-Tiles at home, try making different arrangements with one atop the other and seeing when they stick together.)
Solution
The seemingly magic behavior of the tiles tells us a lot about how magnets A-H must be oriented. Because they’re impervious to rotations, magnets A, C, E, and G must have the same orientation, as must B, D, F, and H. This means we can focus on the orientations of one side.
Imagine we stack two tiles so that A is atop A and B is atop B. This is an attractive arrangement and so must place N with S. This rules out horizontal orientations. Suppose magnet A was arranged with S on the left and N on the right. Then magnet A on the bottom would need to have the opposite arrangement to A on top, a contradiction.
Orientation
So, the magnets must be vertically oriented. Suppose we orient magnet A so that N points up and S down. Since the interaction is unchanged when we flip one of the tiles, magnet B must have the opposite orientation to magnet A.
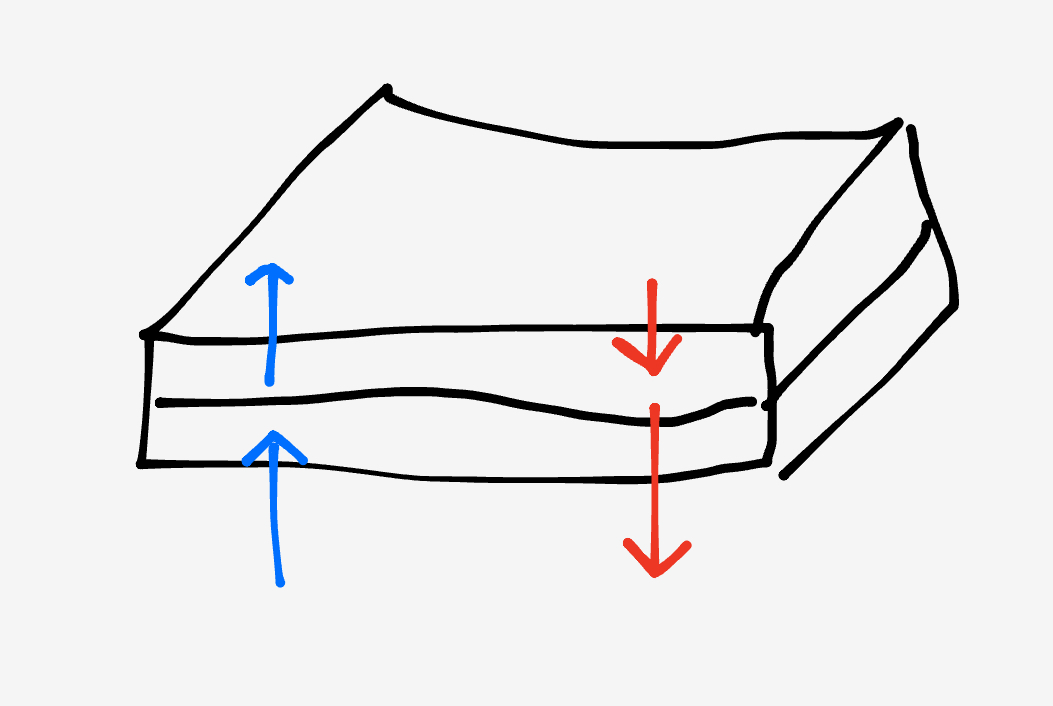
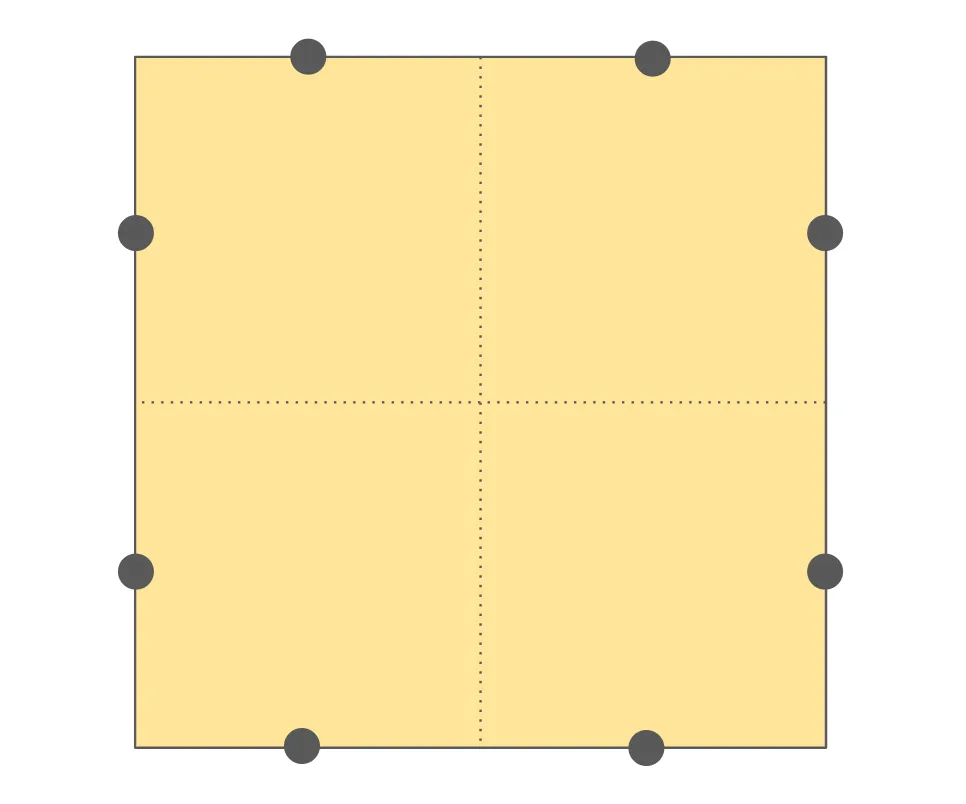
Putting it all together, each tile’s magnets are oriented like so:
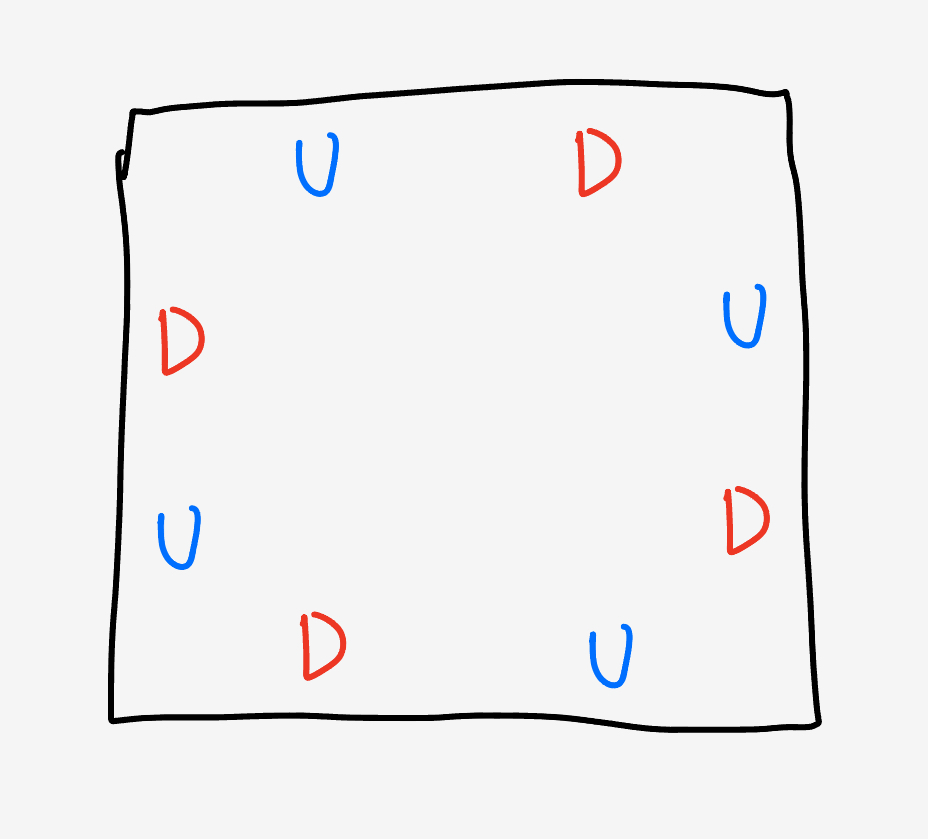
where U/D means the magnet’s north/south end is up.
Stable attachments
Two magnatiles snap tightly together when they’re perfectly overlapped.
But if you push them out of this configuration, and slide one tile over the other, you feel attraction to a few other configurations. Likewise, if you try to slide them out of these configurations you’ll feel resistance.
This is stability. A configuration is stable if the tiles resist small movements away from it. The reason a configuration is stable is that, compared to all its neighboring configurations, the attractive N-S magnet head pairs are as close together as possible while the repulsive N-N and S-S magnet head pairs are as separated as possible.
To explore other configurations, we just need to translate and rotate one tile while keeping the other one fixed. But to find alternate configurations, we need to be able to specify them. We can specify a configuration by the displacement of the sliding tile’s center of mass $\mathbf{r} = \left(x,y\right)$, and its rotation about its center of mass $\theta.$
Setting up the tiles
Given the arrangement of magnets we figured out above, their orientations are
ors = { 1, -1, 1, -1, 1, -1, 1, -1 };
and their locations on the tile are given by
locs[z_]:=
{
{0.25, 1, z}, {0.75, 1, z}, {1, 0.75, z}, {1, 0.25, z}
, {0,75, 0, z}, {0.25, 0, z}, {0, 0.25, z}, {0, 0.75, z}
};
where $z$ keeps track of the vertical separation between the planes of the two tiles.
Rotations and translations
As we said above, sliding the tile around amounts to spinning and translating all the coordinates of the tile:
locsRotAndTrans[x_, y_, theta_, locs_]:=(
COM = {0.5, 0.5, 0};
locsCOM = Table[
locs[[j]] - COM
, {j, 1, 8}];
locsCOMRot = Table[
RotationMatrix[theta, {0, 0, 1}] . locsCOM[[j]]
, {j, 1, 8}];
locsRot = Table[
locsCOMRot[[j]] + COM
, {j, 1, 8}];
locsRotTrans = Table[
locsRot[[j]] + {x, y, 0}
, {j, 1, 8}];
Return[locsRotTrans];
)
The interaction between two tiles is the sum of the interactions between the component magnets on either tile.
\[E = \sum\limits_{i,j\in\{A\,\ldots,H\}} \frac{o_io_j}{\ell_{ij}}\]where the $o_i$ are the orientations we defined above, and $\ell_{ij}$ is the displacement between the tile locations we defined above:
locsRT = rotAndTransLocs[x, y, theta, locs[-0.05]];
interaction =
Sum[
ors[[i]] * ors[[j]] / Norm[locs[0.05][[i]] - locsRT[[j]]]
, {i, 1, 8}
, {j, 1, 8}
];
Exploring configuration space
Doing all that gets us the two tile’s interaction energy $E$ parameterized in terms of $x$, $y$, and $\theta$: $E(x,y,\theta).$ This forms a landscape of energies where depressions in the landscape correspond to the stable arrangements we’re trying to find.
For example, if we hold $\theta$ fixed at zero and vary the position of the second tile’s center of mass, the energy landscape looks like
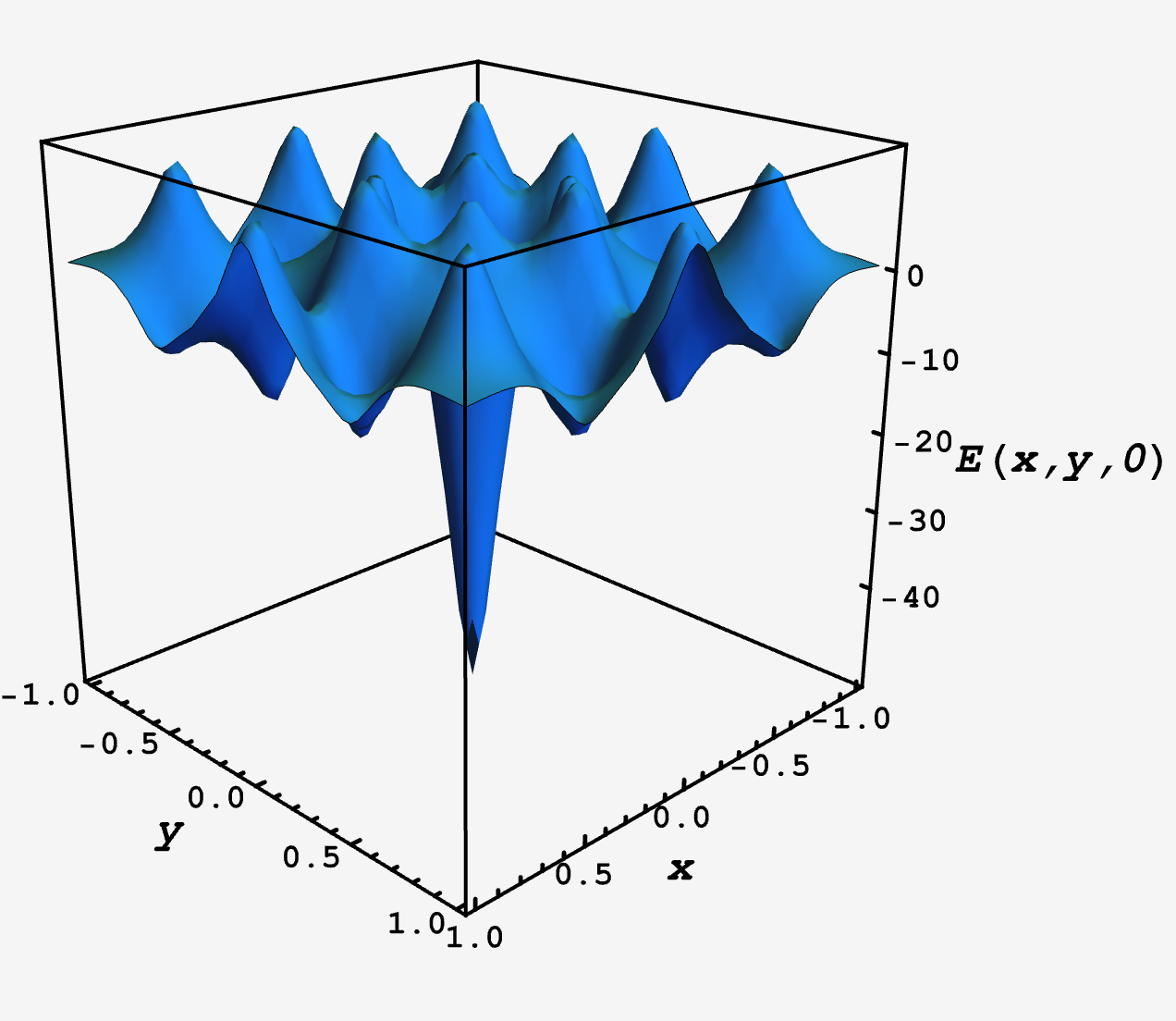
The deep well in the middle is the configuration where the tiles overlap exactly, and it’s surrounded by shallower wells that correspond to lesser stable states.
If, instead, we hold $\theta$ fixed at $\pi/4$ and vary the center of mass, we see a repulsive peak in the center that’s surrounded by shallow wells
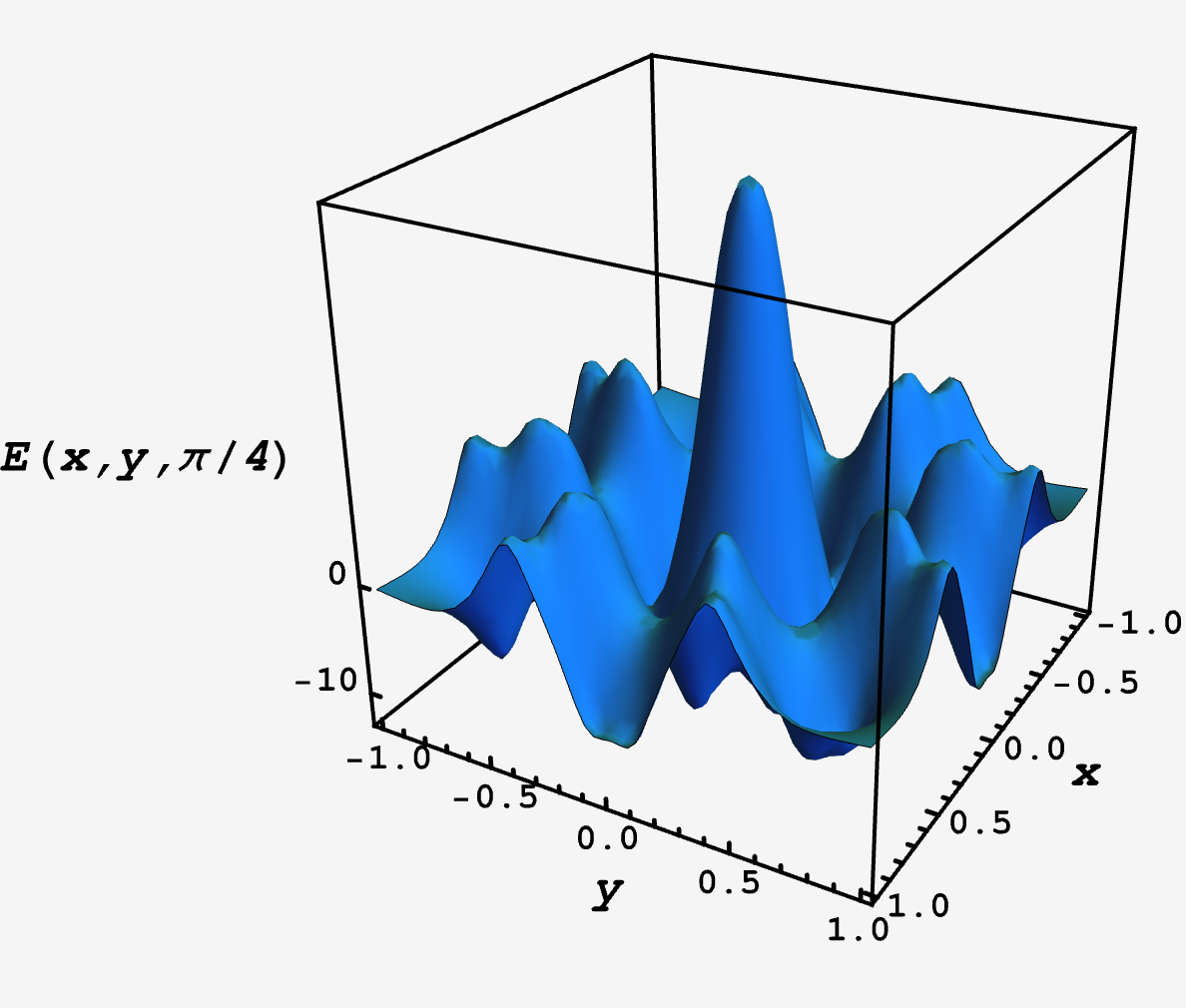
However, these are snapshots at specific values of $\theta$, mere projections of the full space. In general, we can find the stable configurations by following the gradient downhill — start at a random initial position $(x_0, y_0, \theta_0)$ and then take small steps in the direction of steepest descent:
\[\langle x, y, \theta\rangle_t = \langle x, y, \theta\rangle_{t-1} - \eta \nabla E(x, y, \theta).\]Since there are multiple minima, we’ll have to run gradient descent many times, from random starting positions, until we’re pretty sure we’ve found them all (the common ones at least).
Behold the configurations
Carrying this out, we find the four confgurations below:
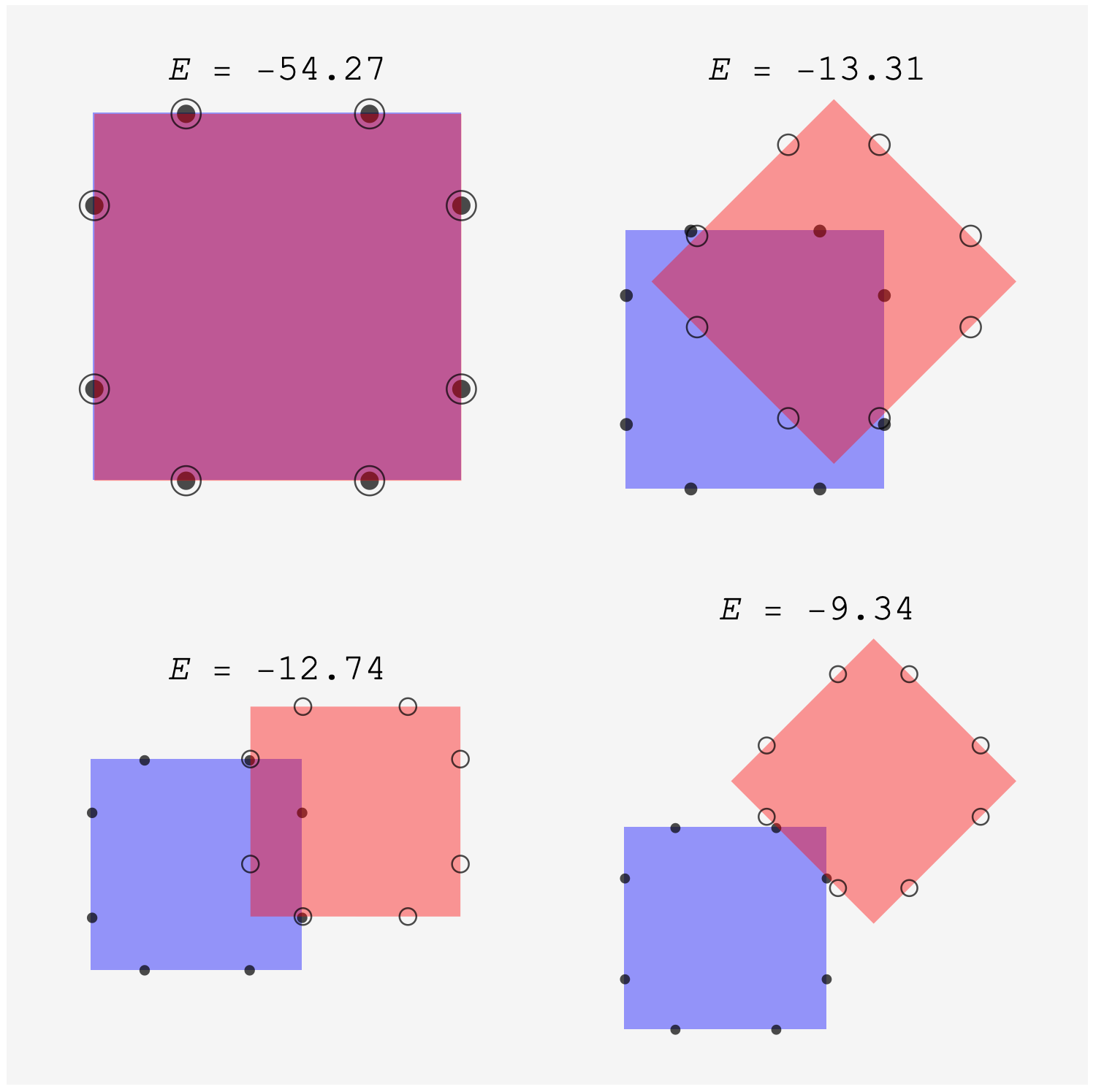
The first is the ultra stable configuration with energy $-54.27$. The second features the red tile pushing a side across the corner of the purple tile until it’s just past the purple diagonal. This places two pairs of opposite monopoles in close proximity for an overall energy of $-13.31$. This is followed closely in third place by an arrangment where adjacent sides overlap so that two monopoles are also in close proximity with overall energy $-12.74$. Finally, there’s an arrangement that’s essentially the second had we stopped sliding the red tile early. This configuration places two opposite monopoles in close proximity, but loses the stabilizing long distance attractive interactions of the first two, yielding an overall energy of $-9.34$.
As it happens, these closely match the stable arrangements you find by sliding two magnatiles in real life. It is really neat how well the model works given the monopole approximation.
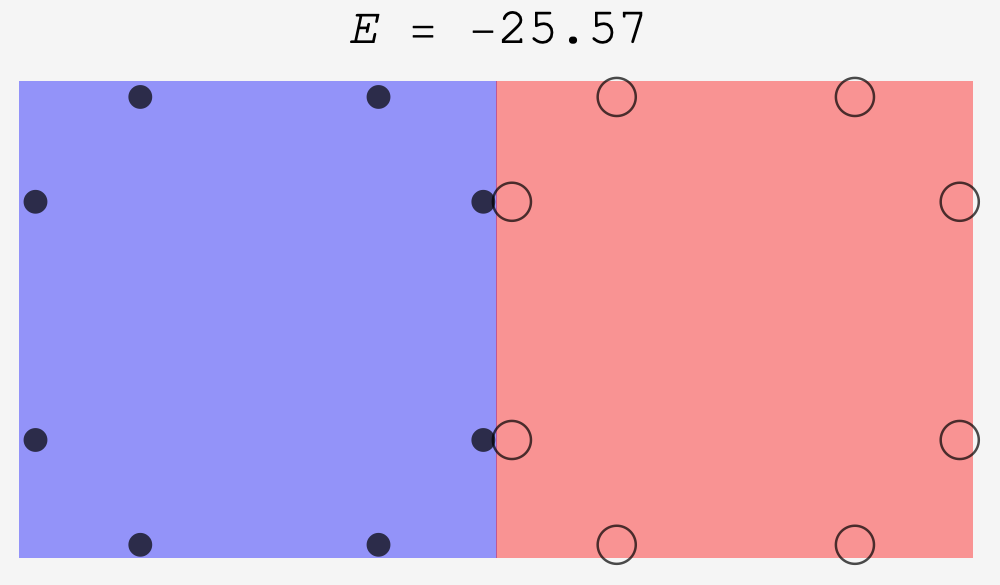
Meet the real number two
With real magnatiles you’ll also find that there’s an even more stable arrangement formed by placing two magnatiles side by side. However, as constructed, our model cannot find or quantify it. The first reason is that our model stipulates the $z$-separation of the tile to be nonzero. The second is that our model puts the monopoles directly at the edge which means there’d be zero distance between them when the tiles are placed side by side. To accomodate this configuration, we made a modified model where the monopoles are pushed in by a small amount ($\delta = 0.03$) from the edge.
When this is done, we find the original stable arrangements with approximately the same energies:
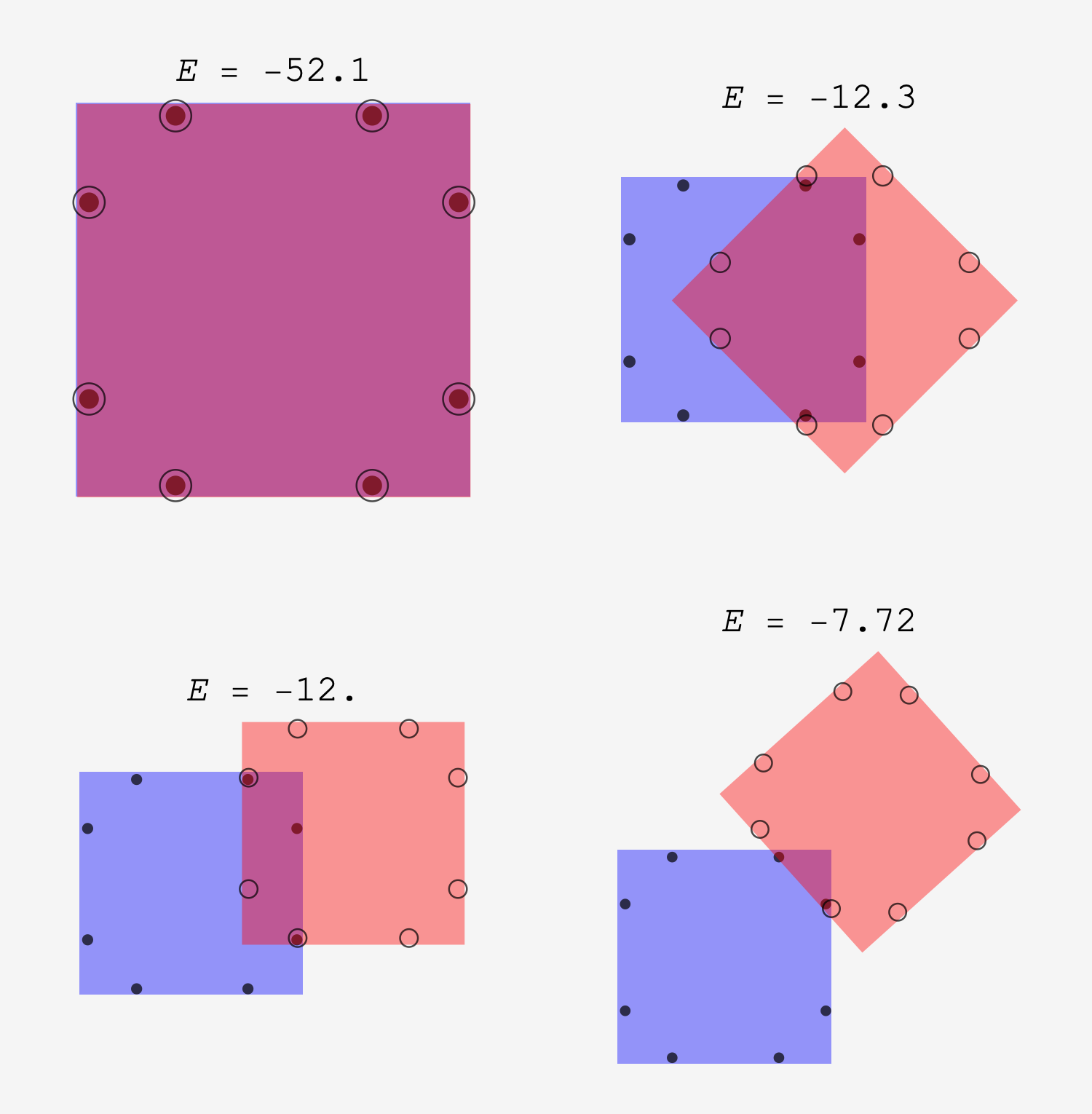
but we can also quantify the stability of the side by side arrangement, which jumps into second place with $E = -25.57$: