Question: You’re doing a $30$-minute workout on your stationary bike. There’s a live leaderboard that tracks your progress, along with the progress of everyone else who is currently riding, measured in units of energy called kilojoules. (For reference, one kilojoule is $1000$ Watt-seconds.) Once someone completes their ride, they are removed from the leaderboard.
Suppose many riders are doing the 30-minute workout right now, and that they all begin at random times, with many starting before you and many starting after. Further suppose that they are burning kilojoules at different constant rates (i.e., everyone is riding at constant power) that are uniformly distributed between 0 and 200 Watts.
Halfway through (i.e., $15$ minutes into) your workout, you notice that you’re exactly halfway up the leaderboard. How far up the leaderboard can you expect to be as you’re finishing your workout?
As an added bonus problem (though not quite Extra Credit), what’s the highest up the leaderboard you could expect to be $15$ minutes into your workout?
Extra credit
Again, suppose there are many riders starting their $30$-minute workouts at random times, and that their powers are uniformly distributed between $0$ and $200$ Watts. Now, suppose you decide that you too will be pedaling with a random (but constant) power between $0$ and $200$ Watts.
If you look down at the leaderboard at a random time during this random workout, how far up the leaderboard can you expect to be, on average?
Solution
We can deal with the extra credit first.
If at any given moment, we polled the rank of every rider currently in the workout, the average rank would just be the $50^\text{th}$ percentile.
However, this is the same question as “if we look down at a random time during a random workout, how far are we up the leaderboard?” because the peloton is the statistical distribution of outcomes for such a random rider.
So the answer to the extra credit is that the random rider finds themself $50\%$ of the way up the leaderboard. This is the same answer we get by integrating over the distribution we find below, but the work is unnecessary.
Standard credit
Now, we want to know where a rider ends up if, halfway through their ride, they find themself halfway up the leaderboard. To deal with this, we need to find the distribution of total energy expenditure for any given random rider.
We can do this by finding the relative volume of riders with energy greater than or equal to $E$ relative to all combinations of power $W$ and elapsed time $t$.
Suppose a rider started at time $t$ and has total energy expenditure greater than or equal to $E.$ That means their power is at least $E/t$ and at most $W_\text{max} = 200\ \text{W}.$ Likewise, such a rider can start their ride as long as $T_\text{max} = 30\ \text{min}$ ago and as short as $E/W_\text{max}\,\text{min}$ ago.
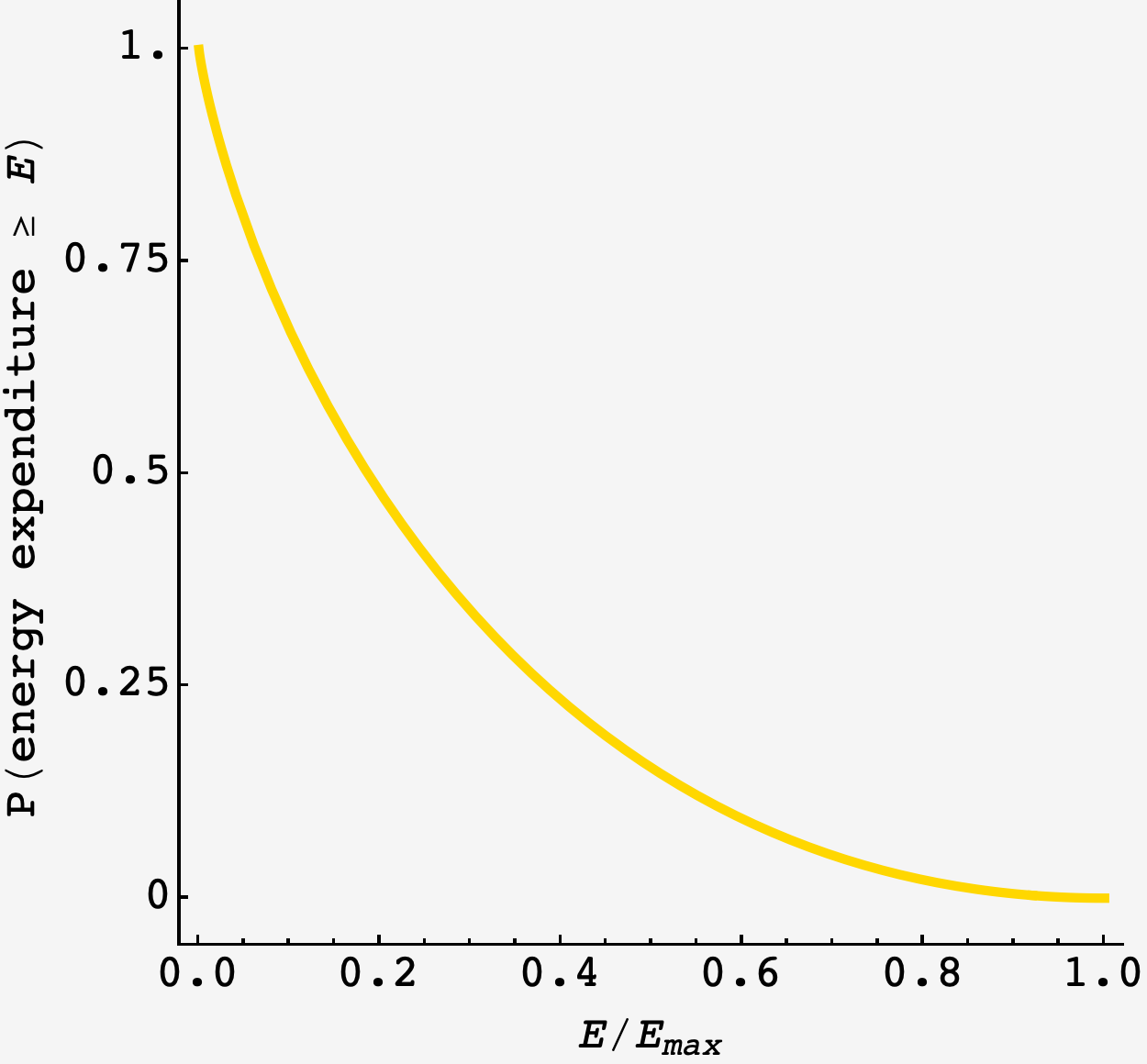
As each rider’s power and start time is uniformly random, we can find $P(\text{rider has energy expenditure }\geq E)$ by integrating over these bounds:
\[\begin{align} P(\text{rider has energy expenditure }\geq E) &= \frac{1}{W_\text{max}T_\text{max}} \int\limits_{E/W_\text{max}}^{T_\text{max}}\text{d}t\, \int\limits_{E/t}^{W_\text{max}}\text{d}W \\ &= \frac{1}{W_\text{max}T_\text{max}} \int\limits_{E/W_\text{max}}^{T_\text{max}}\text{d}t\,\left(W_\text{max} - E/t\right) \\ &= \left(1 - \frac{E}{E_\text{max}}\right) + \frac{E}{E_\text{max}}\log\frac{E}{E_\text{max}} \end{align}\]where $W_\text{max}T_\text{max} = E_\text{max}.$
This is transcendental, so we can numerically solve for the total energy expenditure $E$ that brings this probability to $\frac12$, which yields $E_\text{1/2} = 1120.1\ \text{kJ}.$
Since this is the energy expenditure halfway through the riders run, we double it and plug it back in to find $P(2240.2\ \text{kJ} \geq 2 E_\text{1/2}) \approx 25.9\%$
So, just over $25\%$ of riders will be ahead of this rider at the end of their run.