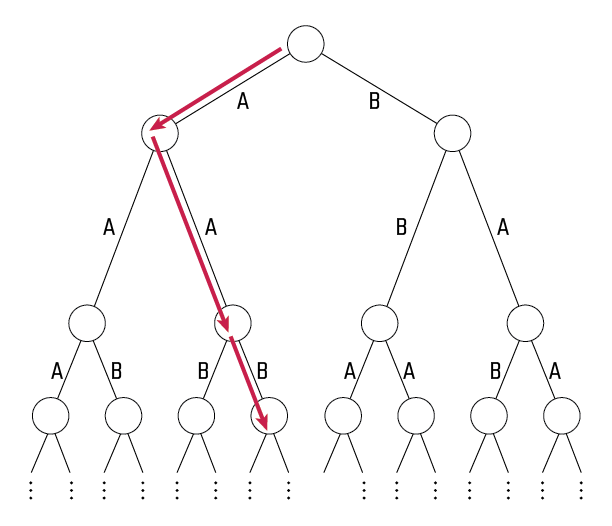
Question: Aaron and Beren are playing a game on an infinite complete binary tree. At the beginning of the game, every edge of the tree is independently labeled $A$ with probability $p$ and $B$ otherwise. Both players are able to inspect all of these labels. Then, starting with Aaron at the root of the tree, the players alternate turns moving a shared token down the tree (each turn the active player selects from the two descendants of the current node and moves the token along the edge to that node). If the token ever traverses an edge labeled $B,$ Beren wins the game. Otherwise, Aaron wins.
An example game is in the picture above: after the labeling, Aaron chooses to go left to avoid immediate defeat, but after Beren goes right Aaron is doomed to choose one of two $B$ paths and Beren wins.
What is the infimum of the set of all probabilities p for which Aaron has a nonzero probability of winning the game? Give your answer in exact terms.
Solution
To get started, let’s look at Aaron and Beren’s positions.
Strategy
Both can somehow inspect the entire tree, so there’s no mystery about what they’ll find in any sub-tree. Beren will win if, at any level, she has a $B$-edge to choose. So, if Aaron is to win, there needs to be at least one path from the beginning to infinity that alternates between one of $\{AA, AB, BA\}$ on the Aaron turns and $AA$ on the Beren turns.
Whenever Beren finishes a turn, we get the original situation back. This means we can look ahead by two steps, and coarse grain over the rest of the turns.
Analysis
Aaron can keep the game going forever if at least one of the branches he sees is infinite.
So, the probability of an infinite game is the probability that one or the other leads to an infinite branch minus the probability that both do:
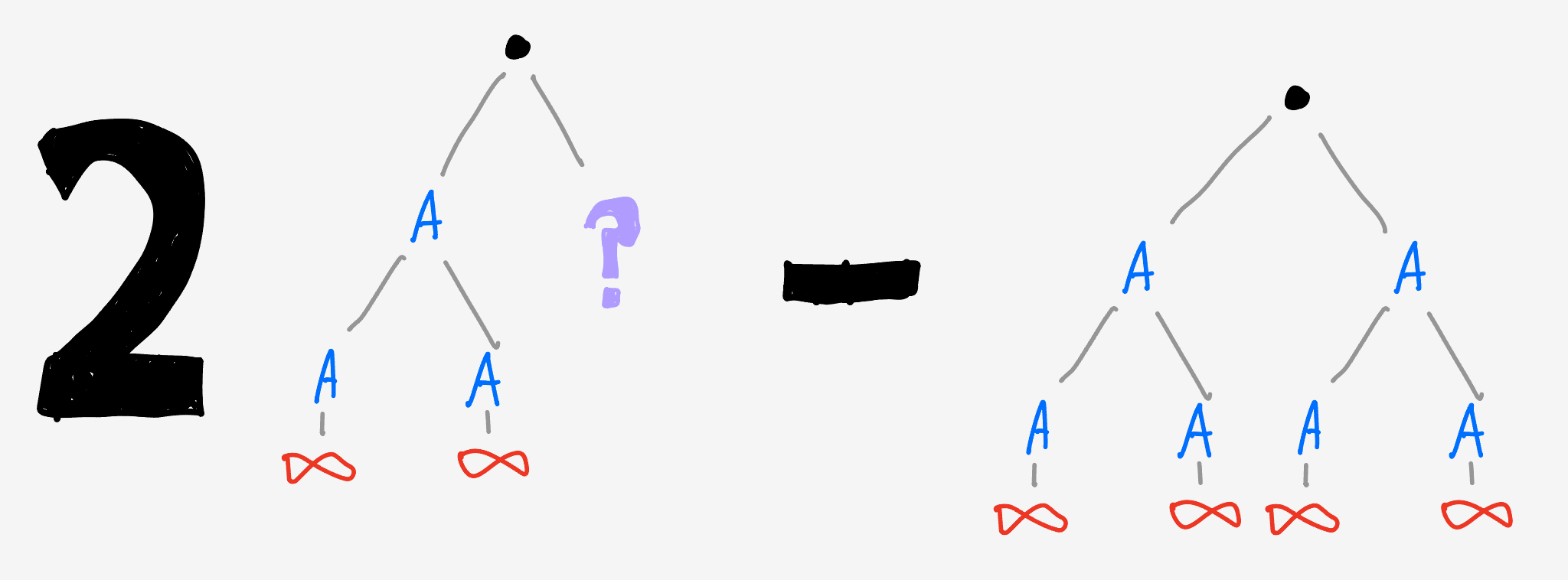
or
\[P_\infty = 2p^3 P_\infty^2 - p^6 P_\infty^4.\]We can divide through by $P_\infty$ (eliminating the trivial $P_\infty = 0$ solution) and rearrange to get
\[0 = p^6 P_\infty^3 - 2p^3 P_\infty + 1.\]Taking the implicit derivative
\[0 = dp (6p^5 P_\infty^3 - 6p^2 P_\infty) + dP_\infty (3p^6 P_\infty^2 - 2p^3)\]shows that $p$ is minimal when $p^3 P_\infty^2 = 2/3.$ Plugging this back in to the original equation, we get $ {\min(P_\infty) = 8/9} $ and, so, the minimum value of $p$ is
\[\begin{align} \min(p) &= \sqrt[3]{2/3 \min(P_\infty)^2} \\ &= \sqrt[3]{27/32}. \end{align}\]In general, $p$ and $P_\infty$ are related through
\[p = \sqrt[3]{\frac{1}{P_\infty + \sqrt{P_\infty^2(1-P_\infty)}}}.\]Conclusions
This outcome is interesting — clearly, the structure of the game favors Beren, so $p$ needs to be pretty high for Aaron to have a chance at all. But we might naively expect Aaron to start with a small chance at $\min(p)$ that grows as $p$ approaches $1.$
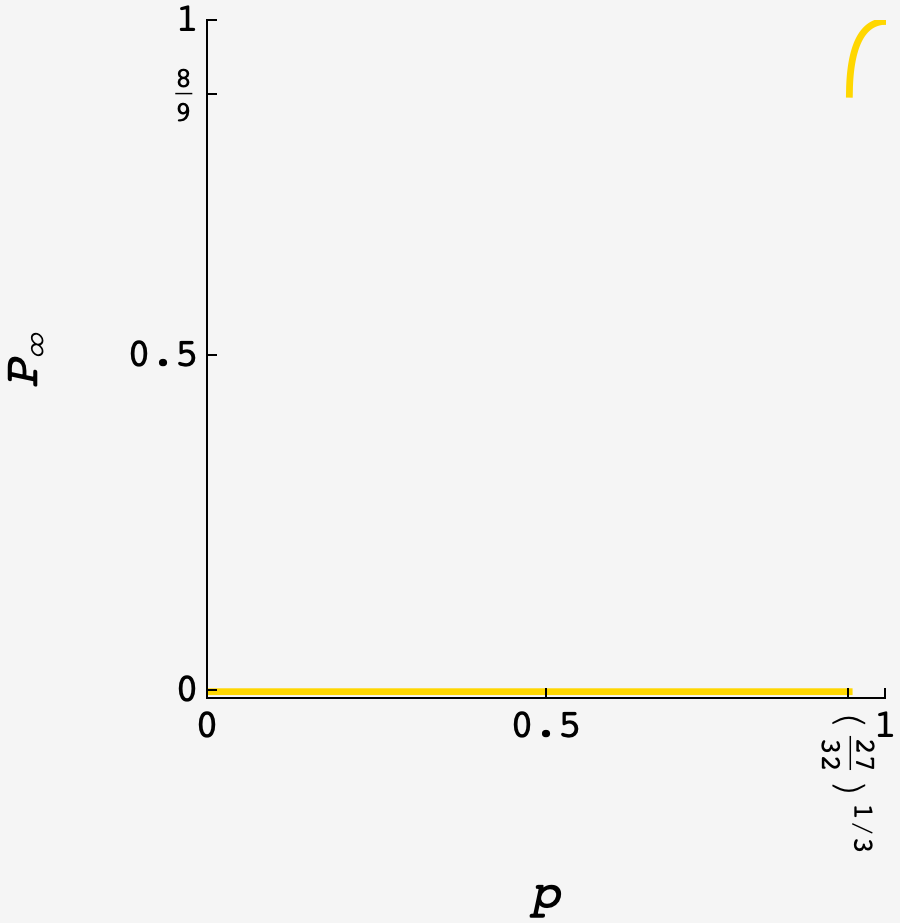
Instead Aaron goes from having no chance at all to suddenly having an $8/9$ chance to win the game as $p$ crosses $\min(p),$ reminiscent of first order phase transitions in physics.
Another interesting thing is that the lowest probability to win is $8/9,$ a simple fraction that doesn’t appear to have a simple justification.