Question: In artistic gymnastics, competitors earn two subscores: one for difficulty and one for execution. Difficulty, as its name implies, is a measure of how challenging a routine is. While there’s technically no upper bound on the difficulty score, the toughest routines will earn around $6$ or $7$ points, depending on the apparatus. Meanwhile, execution scores have a maximum value of $10,$ essentially measuring how cleanly a competitor performed their routine.
What’s weird (to me at least) about gymnastics scoring is that the total score is difficulty plus execution, rather than difficulty times execution.
Why is that weird? Suppose two gymnasts have the same execution score, (say, $8.0$ out of $10$), but one’s difficulty is $20%$ greater (say, $6.0$ to $5.0$). You’d expect that gymnast’s overall score to be $20$ percent greater, right? But instead, because we’re adding the two subscores, there’s only a $7.7$ percent difference in overall score ($14.0$ to $13.0$).
I guess no one is claiming that the total score should scale linearly with both difficulty and execution. But, you know, it really should.
This past week, Brazil’s Rebeca Andrade won the gold medal for her floor routine while American Simone Biles earned the silver. Andrade’s total score was $5.9 + 8.266,$ or $14.166,$ and Biles’ was $6.9 + 7.233,$ or $14.133.$ (Don’t get me started on the rounding.) But if you had multiplied their subscores (like a rational human being), Biles would instead have come out on top, $49.9$ to $48.8.$
So yeah, the decision to add versus multiply the subscores really matters.
Suppose gymnast A has a difficulty score of $6.0,$ while gymnast B has a difficulty score of $5.0.$ If both gymnasts receive independent, random execution scores between $0$ and $10$ (quite the range, I know), what is the probability that their relative ranking would be the same, regardless of whether the subscores were added or multiplied? (Here, you should assume the execution scores are real numbers that can go to any number of decimal places.)
Extra Credit
In addition to their execution scores, now assume that both difficulty scores are now also independent, random values between $0$ and $10$ (again, quite the range).
What is the probability that their relative ranking would be the same, regardless of whether the subscores were added or multiplied? (Again, assume all subscores are real numbers that can go to any number of decimal places.)
Solution
The premise reasonably claims that each “unit” of execution should be valued by its difficulty, rather than what’s done which is to crudely add the execution and difficulty scores.
Let’s take up the mantle of this alternative scoring system and see how often it would turn the tide. Call the execution and difficulty scores of the two gymnasts $(e_1, d_1)$ and $(e_2, d_2).$
For the two systems to come up with different results, we’d need either player to win in either system.
Setting up the calculation
Let’s say Player 1 wins in the additive scheme and Player 2 in the multiplicative one, then
\[e_1 + d_1 > e_2 + d_2,\]and
\[e_1 d_1 < e_2 d_2.\]We can solve either of these for $e_1$ in terms of $e_2$ and the difficulty scores, giving $e_1 + (d_1 - d_2) > e_2 $ and $ e_2 > e_1 d_1/d_2 $ which gives us upper and lower bounds on $e_2.$
Geometry
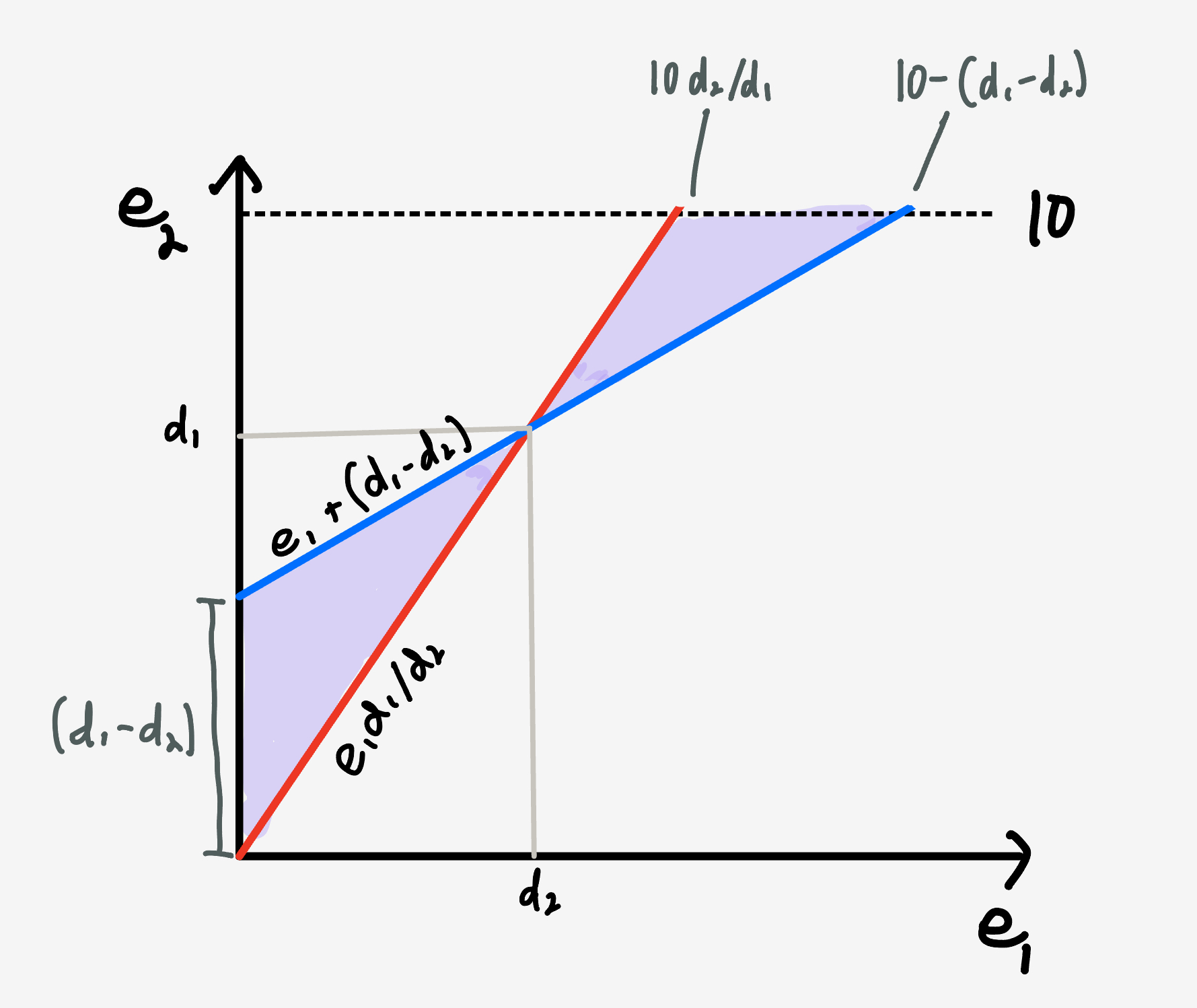
The first one is a line of slope $1$ that leaves the $e_2$-axis from intercept $(d_1 - d_2)$ while the second is a line from the origin with slope $d_1/d_2.$ So, the two bounds approach each other, and form a wedge in $(e_1,e_2)$ space corresponding to Player 1 winning the additive scoring and Player 2 under multiplicative.
The lines converge when $e_1 = d_2,$ then cross. For $e_1 > d_2,$ the two lines bound another wedge region that corresponds to Player 2 winning under additive scoring and Player 1 under multiplicative.
So, the area corresponding to the multiplicative scheme making a difference are the two purple triangles in the diagram above.
The lower triangle has base $(d_1 - d_2)$ and height $d_2$ while the upper triangle has base $(10 - d_1 + d_2 - 10\frac{d_2}{d_1})$ and height $(10-d_1),$ making the probability of a discrepancy
\[\begin{align} P(\text{winner changes}\rvert d_1,d_2) &= \frac{1}{10^2}\left[\frac12(d_1-d_2)d_2 + \frac12(10-d_1)\left(10-(d_1-d_2)-\frac{d_2}{d_1}10\right)\right] \\ &= \frac{(d_1-d_2)\left(d_1d_2 + (d_1-10)^2\right)}{200d_1} \end{align}\]which comes to $23/600$ for $(d_1,d_2) = (6,5).$
Averaging
To find the overall probability of the winner changing, we can average over all possible $d_1$ and $d_2$. The cases for $d_2 > d_1$ and $d_1 > d_2$ are symmetric, so we can just average over $10 > d_1 > d_2$:
\[\begin{align} P(\text{winner changes}) &= \dfrac{\displaystyle\int\limits_0^{10} \text{d}d_1\int\limits_0^{d_1} \text{d}d_2\, P(\text{winner changes}\rvert d_1,d_2)}{\displaystyle\int\limits_0^{10} \text{d}d_1\int\limits_0^{d_1} \text{d}d_2} \\ &= \frac{1}{12}, \end{align}\]which shows there is a $1$ in $12$ chance for the multiplicative scheme to diverge from the usual scoring system.