Question: Consider a three-set tennis match. To win the match, you must win at least two of the three sets. To win a set, you must win a certain number of games. To win a game, you must win a certain number of points. For those who are unfamiliar with tennis, I’ll go into a little more detail.
A game is won by the first player who scores four points. However, the winner must “win by two.” So if both players have three points, they keep going until one player has two more points than their opponent, at which point the player with more points wins the game.
A set is won by the first player to win six games within the set. However, if both players have exactly five games each, then they play exactly two more games. If one player wins both of them, that player wins the set. If each player wins one of these games, so that they now have six games apiece, they proceed to a tiebreak.
A tiebreak is essentially a game that goes to seven points rather than four. The first to seven points wins, and players must win by two.
Assume a three-set tennis match features two players who are evenly matched, so that each player has a $50$ percent chance of winning any given point. Also, points are independent, so the outcome of one point doesn’t affect the probability of who wins subsequent points.
How likely is it that one of the players loses a majority of the points in a match while winning the match itself? (Here, I mean a strict majority, i.e., more than $50$ percent of the points.)
Solution
To solve this, we’re going to directly build the probability distribution for the winner’s score gap.
To do that, we’re going to use partition functions to keep track of the probabilities of all possible outcomes for each class of event.
Before we start, let’s summarize the $\text{GAME}\rightarrow\text{SET}\rightarrow\text{MATCH}$ scheme of tennis.
At the base level we have games, which are played to $4$ (or $7$ for a special kind of playoff game) and are won by getting the balance of the points. We then have sets which are won by getting a balance of the game. Finally, we have matches which are won by getting a balance of the games.
Games can be modeled independently of sets, sets are modeled in terms of games, and matches in terms of sets.
To start, let’s figure out the probabilities of outcome for games.
Games
A normal game is first to $4,$ while winning by at least $2.$ This means that the winner can win by either $4$ (by winning the first four games), by $3$ (by winning three of the first four, followed by winning the fifth game), or by $2$ (any of the remaining possibilities).
This means that the probability distribution for games looks like
\[\begin{align} P_g(4) &= \frac{1}{2^4} = \frac{1}{16} \\ P_g(3) &= \binom{4}{1}\frac{1}{2^5} = \frac18 \\ P_g(2) &= \frac12 - P_g(3) - P_g(4) = \frac{5}{16}. \end{align}\]From these we can form the partition functions, where we attach the probability for a score gap of $j$ to a term $s^j:$
\[Z_\text{win} = 2\left(s^2 \frac{5}{16} + s^3 \frac{1}{8} + s^4 \frac{5}{16}\right)\]Likewise, the possibilities for the score gap of a loser are $Z_\text{win}$ with $s$ mapped to $1/s:$
\[Z_\text{loss} = 2\left(\frac{1}{s^2} \frac{5}{16} + \frac{1}{s^3} \frac{1}{8} + \frac{1}{s^4} \frac{5}{16}\right)\]Playoff games are similar, except the range for the score gap goes from $7$ down to $2,$ with the same logic determining the counting:
\[\begin{align} P_g(7) &= \frac{1}{2^7} \\ P_g(6) &= \binom{7}{1} \frac{1}{2^8} \\ P_g(5) &= \binom{8}{2} \frac{1}{2^9} \\ P_g(4) &= \binom{9}{3} \frac{1}{2^{10}} \\ P_g(3) &= \binom{10}{4}\frac{1}{2^{11}} \\ P_g(2) &= \frac12 - \sum_j P_g(j) \end{align}\]with similar partition functions $Z_\text{playoff win}$ and $Z_\text{playoff loss}$ formed from them.
Since each partition function keeps track of the probabilities for independent alternatives, the partition function for two subsequent events is just the product of the individual partition functions.
Sets
A set is awarded to the first player to win $6$ games, winning by at least $2$ games.
Keeping track of sets according to the number of games won and lost by the winner, $(w,\ell),$ this gives us sets $(6,0),(6,1),(6,2),(6,3)$ and $(6,4)$ for which there are $\binom{w+\ell-1}{\ell}$ ways to order the wins and losses.
The partition functions representing these outcomes is given by
\[Z_{w,\ell} = \binom{w+\ell-1}{\ell}Z_\text{win}^wZ_\text{loss}^\ell.\]If a set gets to $(5,5)$ then it goes to a two game playoff.
If the same player wins both games, then they win the set. This outcome has $\binom{10}{5}$ possible orders and the possible outcomes are given by
\[\binom{10}{5} Z_\text{win}^7 Z_\text{loss}^5.\]The other possibiltiy is that the players split the two playoff games, and the game goes into a one game playoff. The one game playoff has distinct outcomes from the regular games, so the possibilities are given by
\[\binom{10}{5}\binom{2}{1}Z_\text{win}^6 Z_\text{loss}^6 Z_\text{playoff win}.\]Putting this all together, the partition function for all possible winning sets is
\[Z_\text{set win} = \small 2\left[Z_\text{win}^6 + \binom{6}{1}Z_\text{win}^6Z_\text{loss} + \binom{7}{2}Z_\text{win}^6Z_\text{loss}^2 + \binom{8}{3}Z_\text{win}^6Z_\text{loss}^3 + \binom{9}{4}Z_\text{win}^6Z_\text{loss}^4 + \binom{10}{5} Z_\text{win}^7 Z_\text{loss}^5 + \binom{10}{5}\binom{2}{1}Z_\text{win}^6 Z_\text{loss}^6 Z_\text{playoff win}\right].\]and $Z_\text{set loss}$ is found by replacing $s$ with $1/s$ in $Z_\text{set win}.$
Match
With all the legwork out of the way, the match is straightforward.
A match can be won by winning the first two games in a row, or by losing either of the first two sets, followed by winning the third set, so
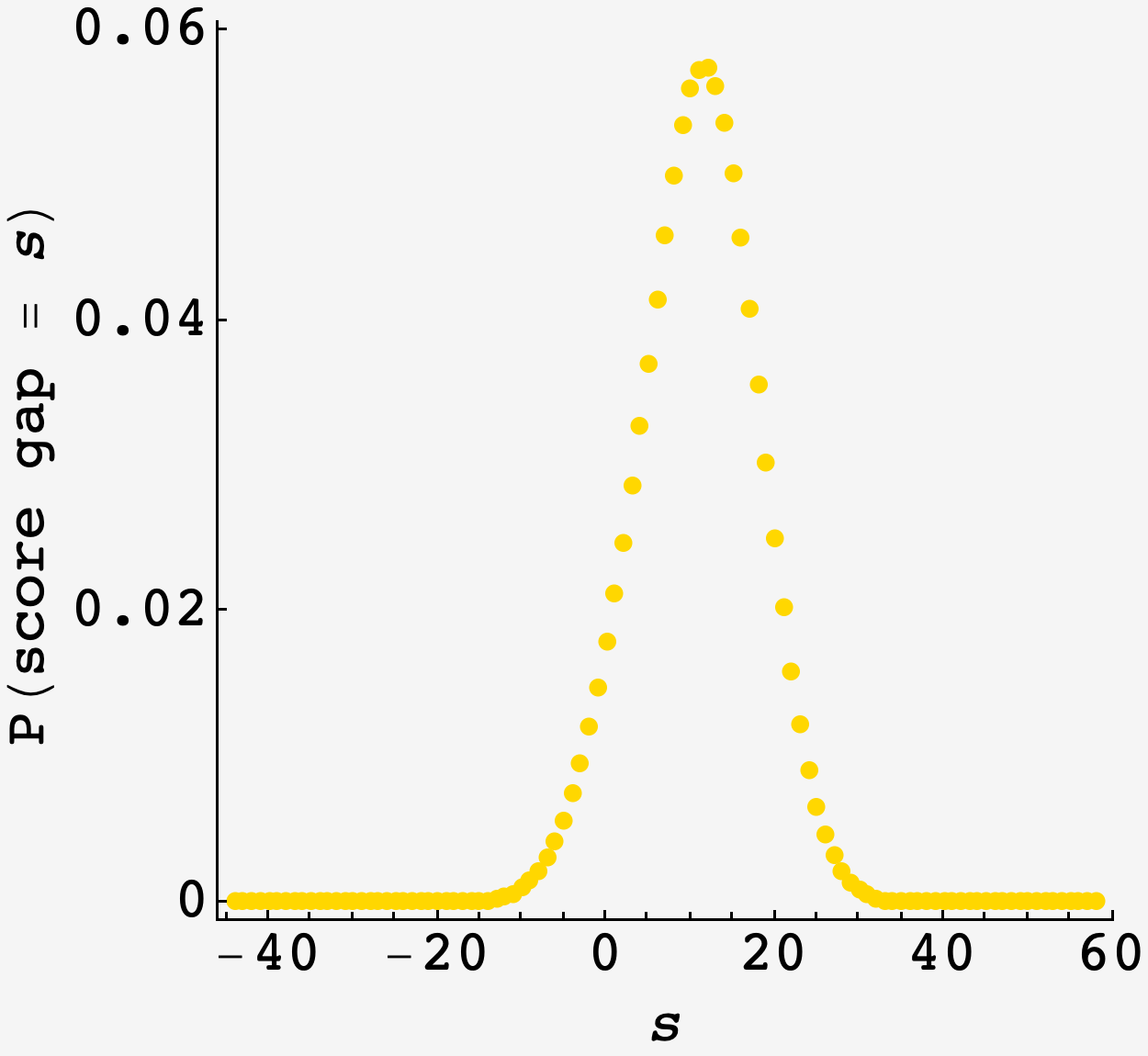
\[Z_\text{match win} = \frac{1}{2!}Z_\text{set win}^2 + \frac{1}{2!}Z_\text{set win}^2 Z_\text{set loss}.\]Expanding this expression, the coefficient on $s^j$ is the probability that the winner ends the match with a score gap of $j.$ To find the probability of winning the match while losing a majority of the points, we can simply select the terms with negative powers:
\[\begin{align} P(\text{win match while losing on points}) &= \sum_{j<0} \left[s^j\right]Z_\text{match win} \\ &= \tfrac{366382889151794439050218364931384718435785359829}{5846006549323611672814739330865132078623730171904} \\ &\approx 0.06267233642 \end{align}\]where $\left[s^j\right]Z$ means to take the coefficient of the $s^j$ term in the series $Z.$
Plotting the full set of coefficients, we get the full probability distribution of score gaps for the winning players: