Question: With The Riddler nearing its end here at FiveThirtyEight, I can finally get something off my chest: Starting a competition with the flip of a coin (say, to determine possession of a ball) is so boring!
Instead, let’s give the captain of one team a fair coin and the captain of the other team a fair die. The captain with the coin will flip it at the same time the other captain rolls the die. They continue doing this until the coin is the same (whether heads or tails) for three consecutive flips or the number that comes face-up on the die is the same for two consecutive rolls.
On average, how many coin flips will it take to get three in a row? And how many die rolls will it take to get two in a row?
Extra credit: While the numbers of flips and rolls may often be the same, which team — the team with the coin or the team with the die — is more likely to win the toss/roll? (That is, which is more likely to happen sooner?)
Solution
We can find the expected number of rolls by accounting for each way we can arrive at a repeat.
Die
For the die, we can either
- immediately repeat the first roll, or
- not repeat the first roll, then go on to eventually repeat.
In the second case we restart the process with a roll under our belt. So, if $T_\text{die}$ is the number of rolls after the first, we get
\[\begin{align} T_\text{die} &= p + (1 - p)(1 + T_\text{die}) \\ &= 1 + (1 - p) T_\text{die} \end{align}\]which leads to $T_\text{die} = 1/p$ and, restoring the first roll, the expected number of rolls to observe a repeat is $T_\text{die}^\prime = 1 + 1/p = 7.$
Coin
For the coin, we can
- immediately observe the same side three times in a row, or
- observe the same side two times in a row, then switch sides, or
- immediately flip sides.
If $T_\text{coin}$ is the number of rolls required after the first, we get
\[T_\text{coin} = 2p^2 + p(1 - p)(2 + T_\text{coin}) + (1 - p)(1 + T_\text{coin})\]which leads to $T_\text{coin} = (1 + p)/p^2 = 6$ and the expected number of rolls to observe three in a row is $T_\text{coin}^\prime = 6 + 1 = 7.$
Surprisingly, these have the same expectation.
Who wins?
To evaluate the race between die rolling and coin flipping, we need to find the distribution of finish times for either medium.
The die is straightforward. Every roll after the first has probability $(1-p)$ to not repeat, and probability $p$ to repeat. So, the probability that the die first repeats on roll $t$ is simply
\[P^\text{die}_2(t) = (1-p)^{t-2}p.\]For the coin, there are more interesting dynamics. If we are seeing a new side at time $t$ (state $1$) it can be because we also saw a new side time $(t-1)$ or because we’d seen two in a row (state $2$) , and then saw a new side at $(t-1):$
\[P_1(t) = (1-p)P_1(t-1) + (1-p)P_2(t-1).\]By contrast, we can only find ourself with two in a row at time $t$ if we were seeing a new side at time $(t-1):$
\[P_2(t) = pP_{1}(t-1).\]Finally, if we finish the game at time $t$ (state $3$) it means that we’d seen the same side two turns in a row at time $(t-1):$
\[P_3(t) = pP_{2}(t-1).\]Solving the system by recurrence
Combining the first and second relations and plugging in our special case of $p=1/2,$ we get
\[P_1(t) = \frac12 P_{1}(t-1) + \frac{1}{2^2} P_{1}(t-2).\]If we define $\widetilde{P}(t) = 2^{t-1} P(t),$ this equation becomes
\[\widetilde{P}_1(t) = \widetilde{P}_{1}(t-1) + \widetilde{P}_{1}(t-2)\]which is just the ordinary Fibonacci sequence, so $P_1(t) = F_t/2^{t-1}.$
Now, using the second and third equations again, we get
\[\begin{align} P_3(t) &= \frac12 P_{2}(t-1) \\ &= \frac{1}{2^2} P_{1}(t-2) \\ &= \frac{F_{t-2}}{2^{t-1}}. \end{align}\]Plotting, we see that state $1$ depletes into state $2$ which depletes into state $3$ (a sequence only spends one time step in state $3$ before being removed from the system):
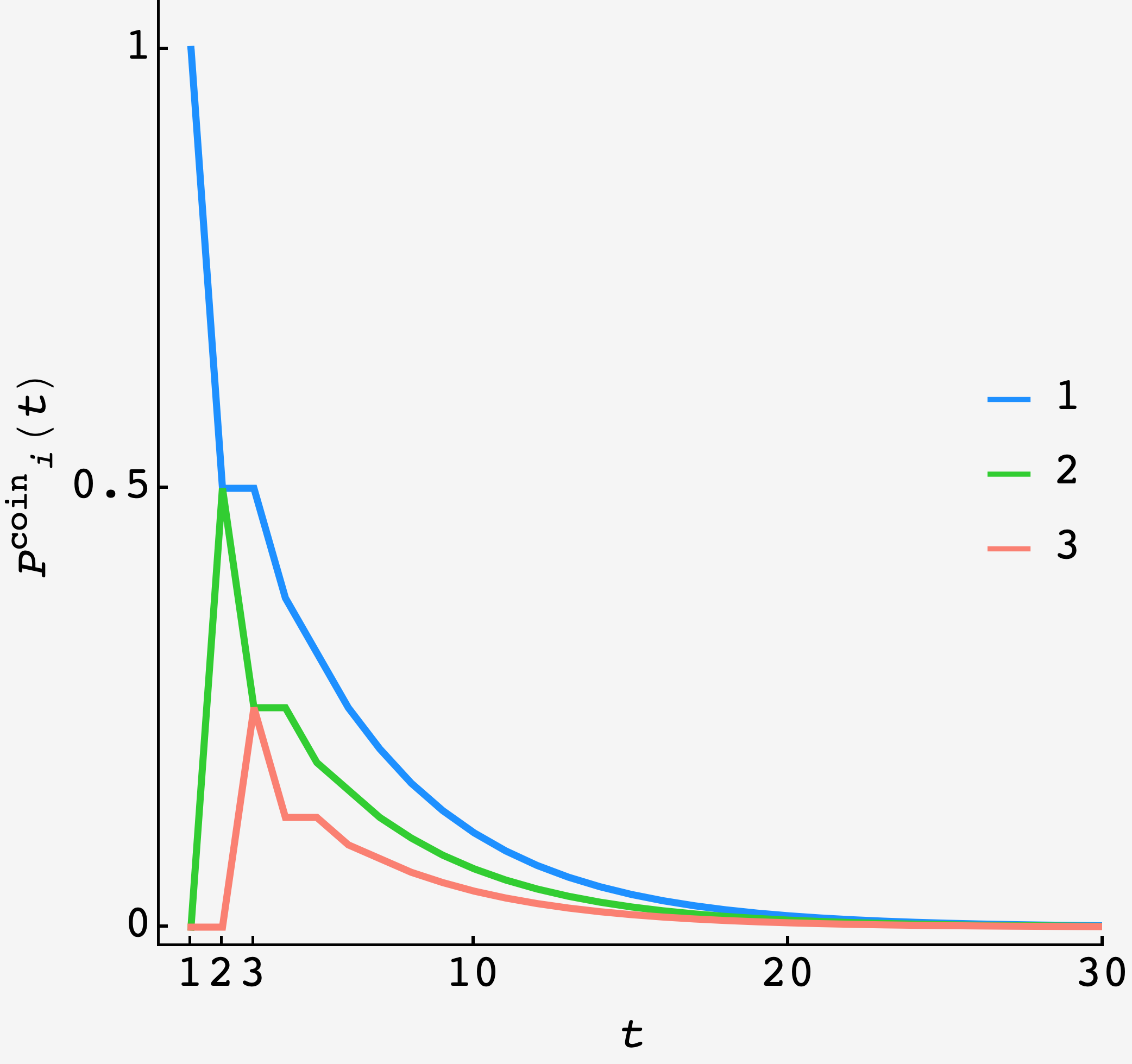
Hat tip to Josh Rose for prodding on this.
Head to head
With $P^\text{coin}_3(t)$ and $P^\text{die}_2(t)$ in hand, we can calculate the probability that the die roller beats the coin flipper.
The die roller wins if they observe the same face twice in a row before the coin flipper sees the same side three times in a row. In other words,
\[\begin{align} P(\text{die wins}) &= P_2^\text{die}(2)\left[P_3^\text{coin}(3) + P_3^\text{coin}(4) + P_3^\text{coin}(5) + \ldots\right] \\ &\, + P_2^\text{die}(3)\left[P_3^\text{coin}(4) + P_3^\text{coin}(5) + P_3^\text{coin}(6) + \ldots\right] + \ldots \\ &= \sum\limits_{i=2}^\infty \sum\limits_{j=i+1}^\infty P_2^\text{die}(i)P_3^\text{coin}(j) \\ &= \sum\limits_{i=2}^\infty P_2^\text{die}(i) \left[1 - \sum\limits_{j=3}^i P_3^\text{coin}(j)\right] \\ &= \frac{29}{59} \end{align}\]Which comes out to approximately $ P(\text{die win}) \approx 0.491525\ldots$ and compares favorably with a $N = 10^8$ run estimate $\hat{P}(\text{die win}) \approx 0.491498\ldots$
We can also evaluate the likelihood that the coin wins through
\[P(\text{coin wins}) = \sum\limits_{i=3}^\infty \sum\limits_{j=i+1}^\infty P_3^\text{coin}(i)P_2^\text{die}(j) = \frac{25}{59} \approx 0.423729\ldots\]Finally, the likelihood of a tie is found by summing
\[\sum\limits_{i=3}^\infty P_3^\text{coin}(i)P_2^\text{die}(i) = 5/59 \approx 0.0847458\ldots\]Solving the system by transform
We can also find $P^\text{coin}_3(t)$ through diagonalization. Packaging the system of equations, we get the linear transformation:
\[\left(\begin{array}{c}P_1(t) \\ P_2(t) \\ P_3(t)\end{array}\right) = \overbrace{\left(\begin{array}{ccc} (1-p) & (1-p) & 0 \\ p & 0 & 0 \\ 0 & p& 0\end{array}\right)}^\mathbf{M} \cdot \left(\begin{array}{c} P_{1}(t-1) \\ P_{2}(t-1) \\ P_{3}(t-1)\end{array}\right)\]We can diagonalize $\mathbf{M}$ so that
\[\mathbf{P}(t) = \mathbf{T}\mathbf{D}\mathbf{T}^{-1}\cdot\mathbf{P}(t-1)\]by placing the eigenvectors of $\mathbf{M}$ as the columns of $\mathbf{T}$
\[\mathbf{T} = \left(\begin{matrix}0 & \frac{p \left(1 - p\right) + \frac{\left(p - 1\right) \left(p + \sqrt{- \left(p - 1\right) \left(3 p + 1\right)} - 1\right)}{2}}{p^{2}} & \frac{p \left(1 - p\right) - \frac{\left(p - 1\right) \left(- p + \sqrt{- \left(p - 1\right) \left(3 p + 1\right)} + 1\right)}{2}}{p^{2}}\\ 0 & \frac{- p - \sqrt{- \left(p - 1\right) \left(3 p + 1\right)} + 1}{2 p} & \frac{- p + \sqrt{- \left(p - 1\right) \left(3 p + 1\right)} + 1}{2 p}\\ 1 & 1 & 1\end{matrix}\right)\]and the eigenvalues of $\mathbf{M}$ as the entries of $\mathbf{D}:$
\[\mathbf{D} = \left(\begin{matrix}0 & 0 & 0\\ 0 & - \frac{p}{2} - \frac{\sqrt{- \left(p - 1\right) \left(3 p + 1\right)}}{2} + \frac{1}{2} & 0\\ 0 & 0 & - \frac{p}{2} + \frac{\sqrt{- \left(p - 1\right) \left(3 p + 1\right)}}{2} + \frac{1}{2}\end{matrix}\right).\]This representation makes it straightforward to generate the occupation of states $1,2,$ and $3$ over time by raising the entries of $\mathbf{D}$ to the power $t.$
\[\mathbf{P}(t) = \mathbf{T}\mathbf{D}^{t-1}\mathbf{T}^{-1}\cdot\mathbf{P}(1)\]Setting $\mathbf{P}(1)$ to $\left(1,0,0\right)^\top$ (all sequences start in state $1$) and dotting the result with $\left(0,0,1\right),$ (all sequences end in state $3$) we can extract $P_3(t).$
Plugging in $p = \frac12$ for the coin, the eigenvalues are $0,$ $\lambda_1 = \frac12\left(\frac12-\frac{\sqrt{5}}{2}\right),$ and $\lambda_2 = \frac12\left(\frac12+\frac{\sqrt{5}}{2}\right).$ Taking the product, we get
\[\begin{align} P_3(t) &= \frac{\left(\frac{1}{2}+\frac{\sqrt{5}}{2}\right) \lambda_1^{t-1}+\left(\frac{\sqrt{5}}{2}-\frac{1}{2}\right) \lambda_2^{t-1}}{\sqrt{5}} \\ &= \left[-\left(\frac{\sqrt{5}-1}{2}\right)^{t-2} + \left(\frac{\sqrt{5}+1}{2}\right)^{t-2}\right]\frac{1}{2^{t-1}\sqrt{5}} \\ &= \frac{F_{t-2}}{2^{t-1}}, \end{align}\]where $F_t$ is the $t^\text{th}$ Fibonacci number.