Question: Assign four nonnegative integers to the corners of a square, which we designate the active square. During a step, for each side of the active square, the absolute difference between the numbers on that side’s endpoints is assigned to its midpoint. Then these four new midpoints are connected into a new square (tilted $45$ degrees from the previous). This new smaller square becomes the active square. Continue these steps until the active square has all zeroes on its corners.
Define $f(a, b, c, d)$ to be the total number of squares drawn during this process when beginning with the numbers $(a, b, c, d)$ written on the starting square in clockwise order. For example, given a starting arrangement of $(10, 6, 3, 1),$ we would get the sequence of
$(4, 3, 2, 9)\rightarrow(1, 1, 7, 5)\rightarrow(0, 6, 2, 4)\rightarrow(6, 4, 2, 4)\rightarrow(2, 2, 2, 2)\rightarrow(0, 0, 0, 0),$
where the game ends (pictured above). So $f(10, 6, 3, 1) = 7.$ And trivially, $f(0, 0, 0, 0) = 1.$
Consider the set $S = \{(a, b, c, d) \rvert a, b, c, d\in\mathbb{Z}, 0 \leq a, b, c, d \leq 10^7\}.$
Let $M$ be the maximum value $f$ obtains on $S.$ Find $(a, b, c, d)$ in $S$ with minimum sum $(a+b+c+d)$ where $f(a, b, c, d) = M.$
Solution
First of all, the map from one square to the next is
\[\left(a,b,c,d\right) \overset{M}{\longrightarrow} \left(\lvert a-b\rvert, \lvert b-c\rvert, \lvert c-d\rvert, \lvert d-a\rvert\right).\]We can follow the map on a couple of squares to get the hang of it:
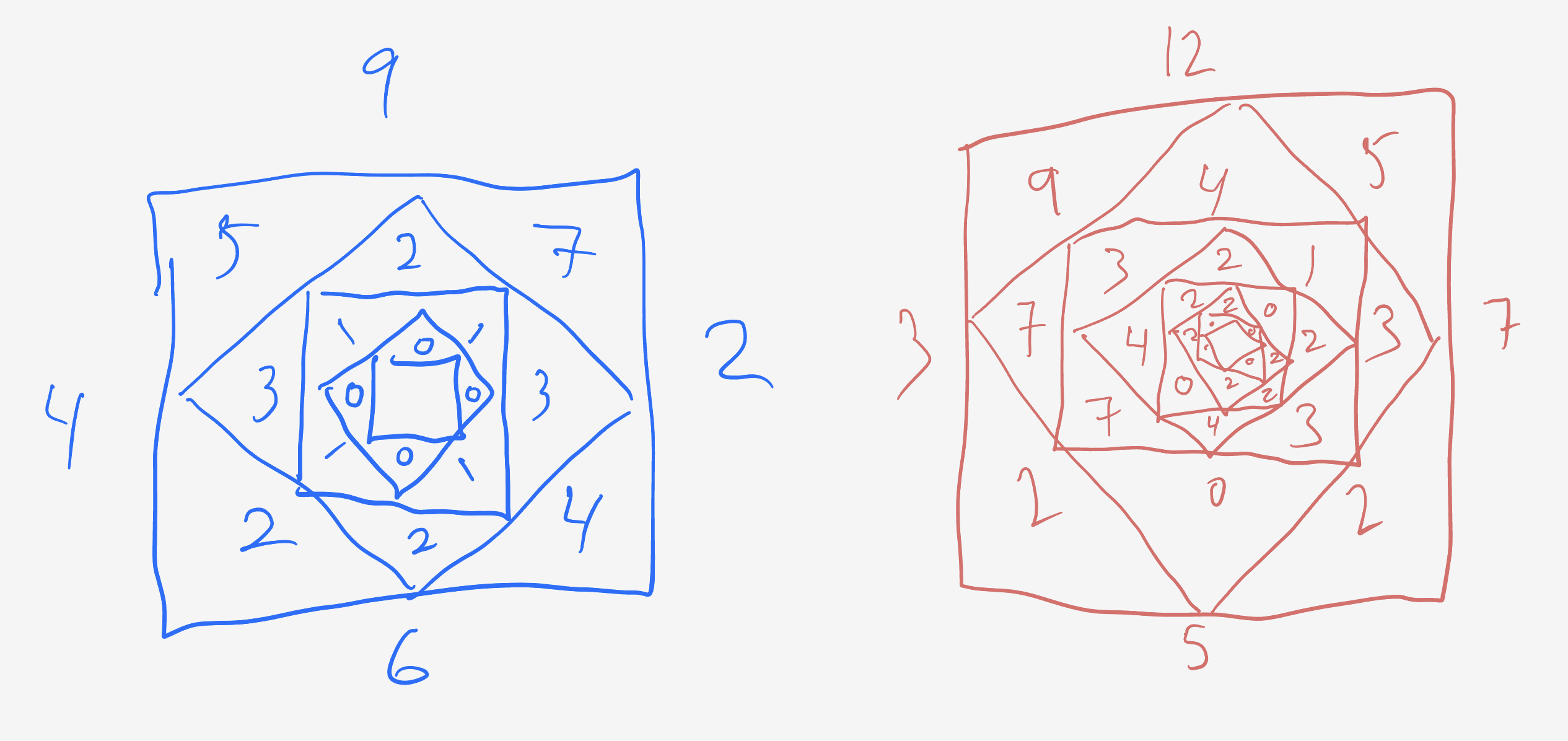
We want to find the starting configuration $(a,b,c,d)$ that takes the most map iterations to reach the $\left(0,0,0,0\right)$ square.
From the map, we can see two properties of $f$:
1 - $f$ is invariant under uniform translations
\[f(a,b,c,d) = f(a+k,b+k,c+k,d+k),\]2 - and $f$ is invariant under uniform scaling
\[f(a,b,c,d) = f(\gamma a, \gamma b, \gamma c, \gamma d).\]The second property shows that we can think of $(a,b,c,d)$ as a relative composition (normalize it so that its components sum to $1$). If we can find a composition $(a,b,c,d)$ that maps back to itself then, in principle, the value of $f$ would be infinite.
We will look for such a composition, and then look for the closest integer approximation we can find. The bigger the numbers we use, the more closely we should be able to approximate the ideal composition.
If $(a,b,c,d)$ maps to itself, then, up to an overall multiplicative constant
\[(a,b,c,d) = \left(\lvert a-b\rvert, \lvert b-c\rvert, \lvert c-d\rvert, \lvert d-a\rvert\right).\]Since the two compositions are the same, ratios between like components are the same as well. Taking the ratio of the first and second components of each composition, we get:
\[\begin{align} \frac{a}{b} &= \dfrac{\lvert a - b\rvert}{\lvert b-c\rvert} \\ &= \frac{a}{b}\dfrac{\lvert 1-\frac{b}{a}\rvert}{\lvert 1-\frac{c}{b}\rvert}. \end{align}\]Which shows that $b/a = c/b.$ The same comparison for the second and third components shows that $c/b = d/c$ as well.
Putting it all together, we have shown that $a = b/\gamma = c/\gamma^2 = d/\gamma^3,$ which shows that $(a,b,c,d)$ is monotonic.
Now, if we compare the first and fourth components, we get (assuming $a>b>c>d,$ and therefore $\gamma > 1$):
\[\begin{align} \frac{d}{a} &= \dfrac{\lvert d-a\rvert}{\lvert a-b\rvert} \\ \gamma^3 &= \dfrac{1 - \gamma^3}{1-\gamma}, \end{align}\]or $2\gamma^3 -\gamma^4 - 1 = 0,$ which has one relevant root
\[\begin{align} \gamma &= \frac13 \left(1 + \sqrt[3]{\left(19 - 3 \sqrt{33}\right)} + \sqrt[3]{19 + 3 \sqrt{33}}\right) \\ &\approx 1.8393\ldots \end{align}\]So, an ideal composition vector is given by
\[\dfrac{1}{1+\gamma+\gamma^2+\gamma^3}\left(1,\gamma,\gamma^2,\gamma^3\right),\]which is stationary under the map, as expected. From here we can just scale up the composition vector, looking for its closest integer approximation, which is
\[\phi = \left(10301680,5600910,3045153,1655616\right).\]Running this through $f$ gets $f(\phi) = 44.$
Because of the first property, we can subtract the minimum entry from each component of the composition vector without changing the value of $f,$ so the vector with minimum sum is
\[\phi = \left(8646064,3945294,1389537,0\right).\]