Reasonable Sandwich

Question: I have made a square peanut butter and jelly sandwich, and now it’s time to slice it. But rather than making a standard horizontal or diagonal cut, I instead pick two random points along the perimeter of the sandwich and make a straight cut from one point to the other. (These points can be on the same side.)

My slice is “reasonable” if I cut the square into two pieces and the smaller resulting piece has an area that is at least one-quarter of the whole area. What is the probability that my slice is reasonable?

(FiveThirtyEight)

Solution

This problem is rooted in the geometry created by the slice, but to solve it we’ll focus on the geometry of the parameter space — the plane defined by $a$ and $b,$ the positions along the sides where each cut is made.

One quarter of the time, $a$ and $b$ are on the same side of the sandwich, and the small piece has size zero.

If $a$ and $b$ are on adjacent sides, which happens $2/4$ of the time, then the smaller sandwich space is a right triangle of area $\frac12ab.$

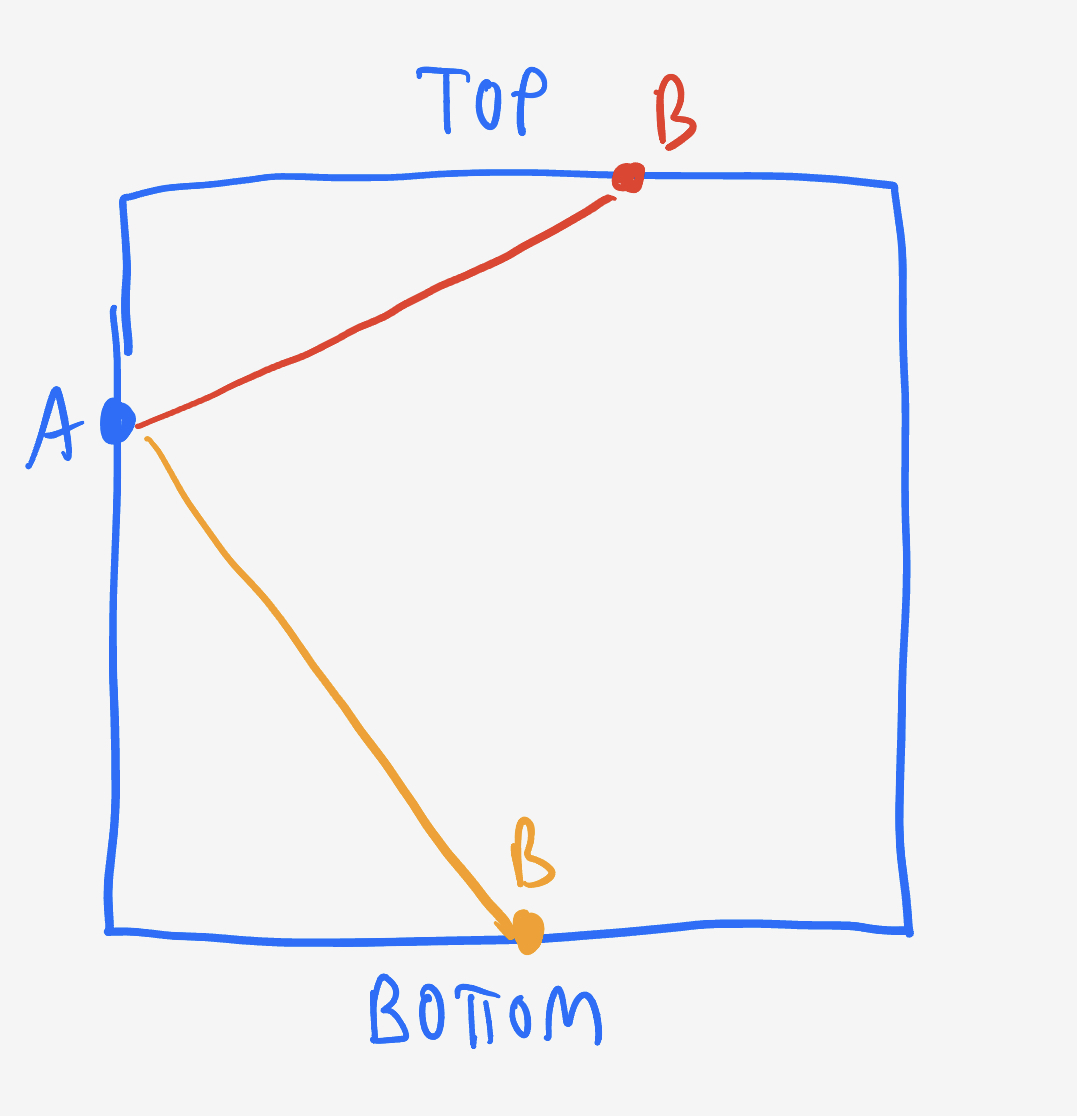
Since we want the small piece to be “reasonable”, we have

The upper bound is only reachable at the point $(a,b) = (1,1),$ so we can focus on the lower bound. multiplying through by $2,$ we get $\frac12 \leq ab,$ or

In the parameter space, this is a curve from the point $(1,\frac12)$ to $(\frac12, 1):$

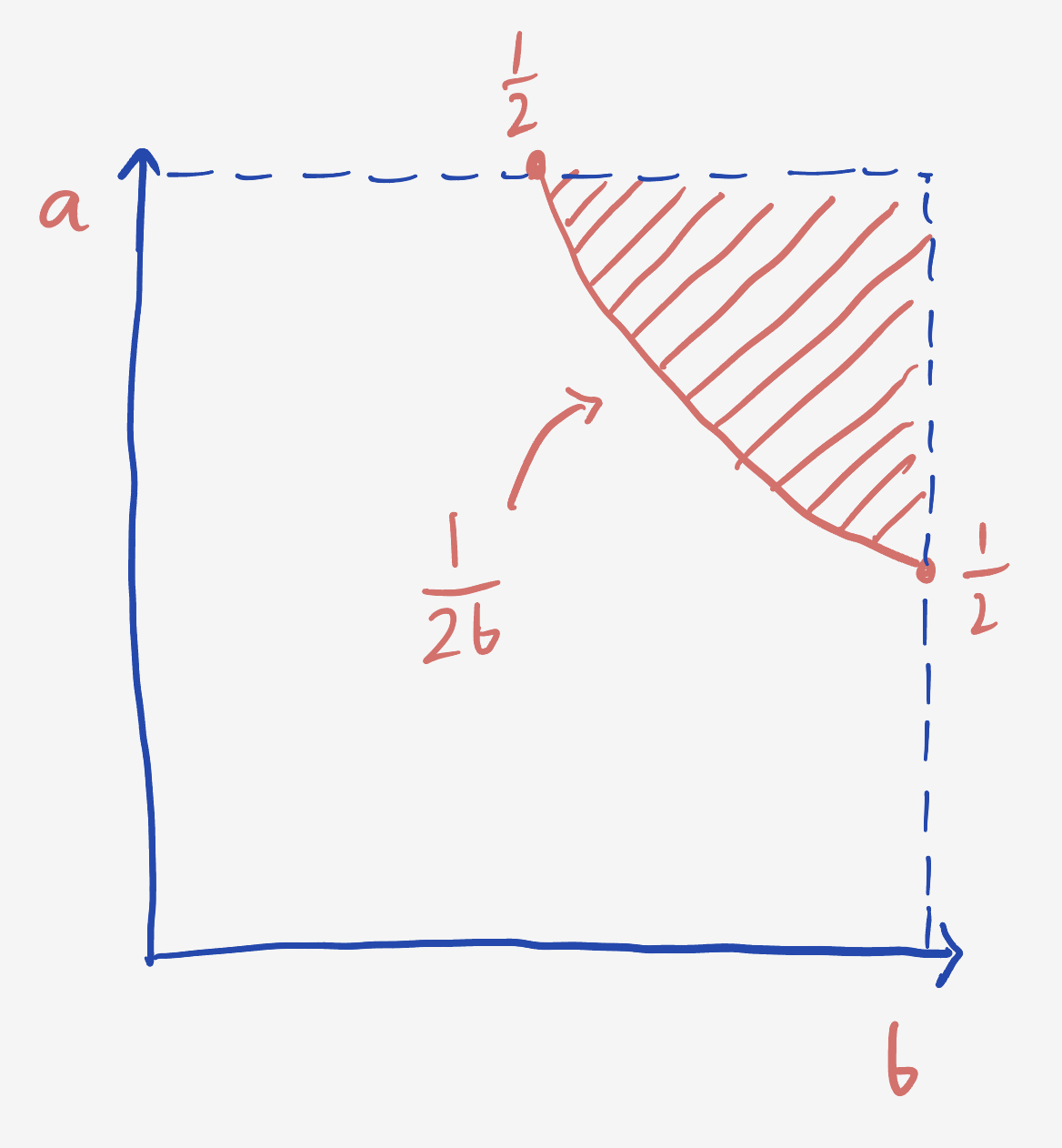
The area under this curve is $\int\limits_0^1 \text{d}b\ a = \frac12 + \int\limits_{\frac12}^1 \frac{\text{d}b}{2b} = \frac12 + \frac{\log 2}{2}.$

The relevant area for “reasonable” small pieces is the complement, so the chance of a reasonable smaller triangle is $\frac12 - \frac12 \log 2.$

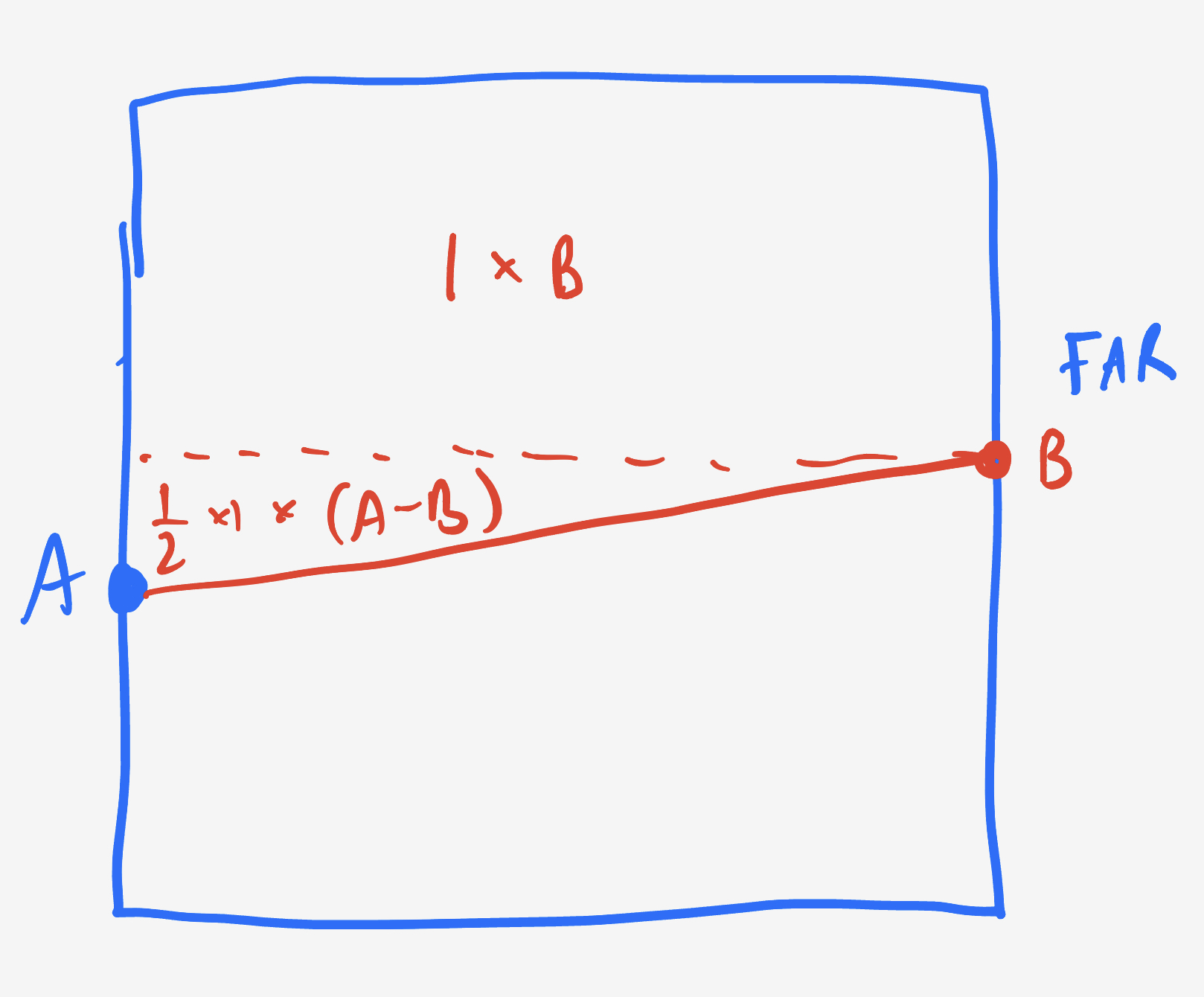
When $a$ and $b$ are on opposite sides, which happens the other $1/4$ of the time, the area is made up of a rectangle and a triangle.

If $a > b,$ then the rectangle has area $1\times b$ and the triangle area is $\frac12 (a-b)\times 1,$ which makes $\dfrac12(a+b).$ When $b > a,$ the roles are reversed, but the expression is the same.

We want the small piece to be “reasonable,” so we’re interested in values of $a$ and $b$ where $\dfrac14 \leq \dfrac12(a+b) \leq \dfrac34.$ This gives us two inequalities: $a \geq \frac12 - b$ and $a \leq \frac32 - b.$ Plotting them, they make a stripe of admissible values in the parameter space that goes diagonally down and to the right.

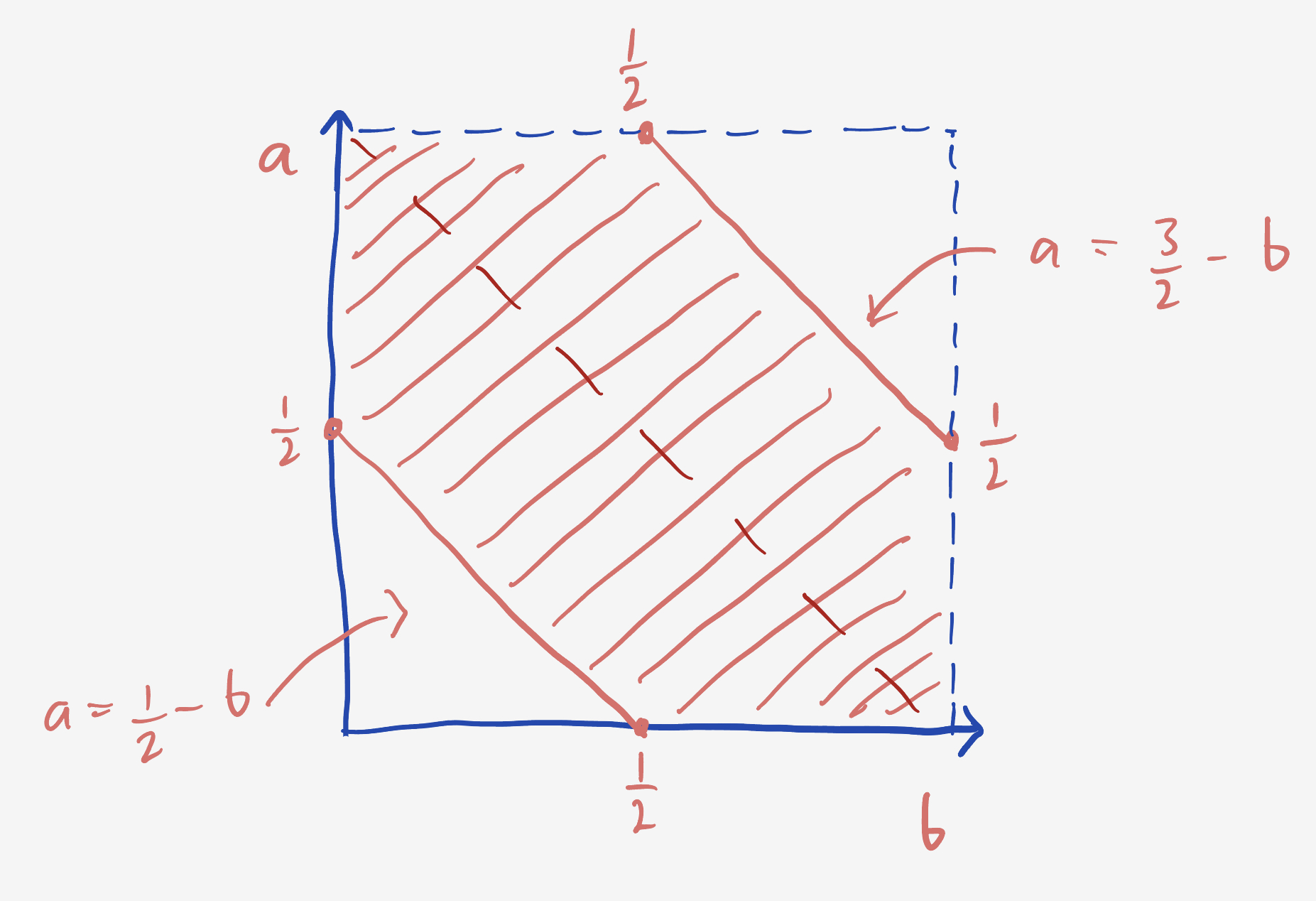
The area of the stripe is just $1 - 2\times \frac18 = 3/4.$

Putting it all together, the total area contributing to $A_\text{small} \geq \frac14$ is

almost a quarter of the time.