Question: A thousand people are playing Lotería, also known as Mexican bingo. The game consists of a deck of 54 cards, each with a unique picture. Each player has a board with $16$ of the $54$ pictures, arranged in a $4$-by-$4$ grid. The boards are randomly generated, such that each board has $16$ distinct pictures that are equally likely to be any of the $54$.
During the game, one card from the deck is drawn at a time, and anyone whose board includes that card’s picture marks it on their board. A player wins by marking four pictures that form one of four patterns: any entire row, any entire column, the four corners of the grid and any $2$-by-$2$ square.
After the fourth card has been drawn, there are no winners. What is the probability that there will be exactly one winner when the fifth card is drawn?
Solution
There are four ways to win the Loteria
- cards on the $4$ corners,
- a row of $4$ cards,
- a column of $4$ cards, or
- a $2\times2$ square of cards.
If we’re to win on the $5^\textrm{th}$ round, we have to be one card placement away from winning on the $4^\textrm{th}$ round. With only $4$ cards drawn, these outcomes are independent, since only one winning pattern can result with $5$ cards in play.
So, we have
\[\begin{align} N(\text{win on }5^\textrm{th}\text{ draw}) &= N(\text{corners }\mathbf{ OR }\text{ row }\mathbf{ OR }\text{ column }\mathbf{ OR }\text{ square}) \\ &= N(\text{corners}) + N(\text{row}) + N(\text{column}) + N(\text{square}) \end{align}\]To do our counting, we’re going to envision everyone’s board as the main $4\times4$ area attached to a $(T-4\times4)$ long strip where the unused cards reside.
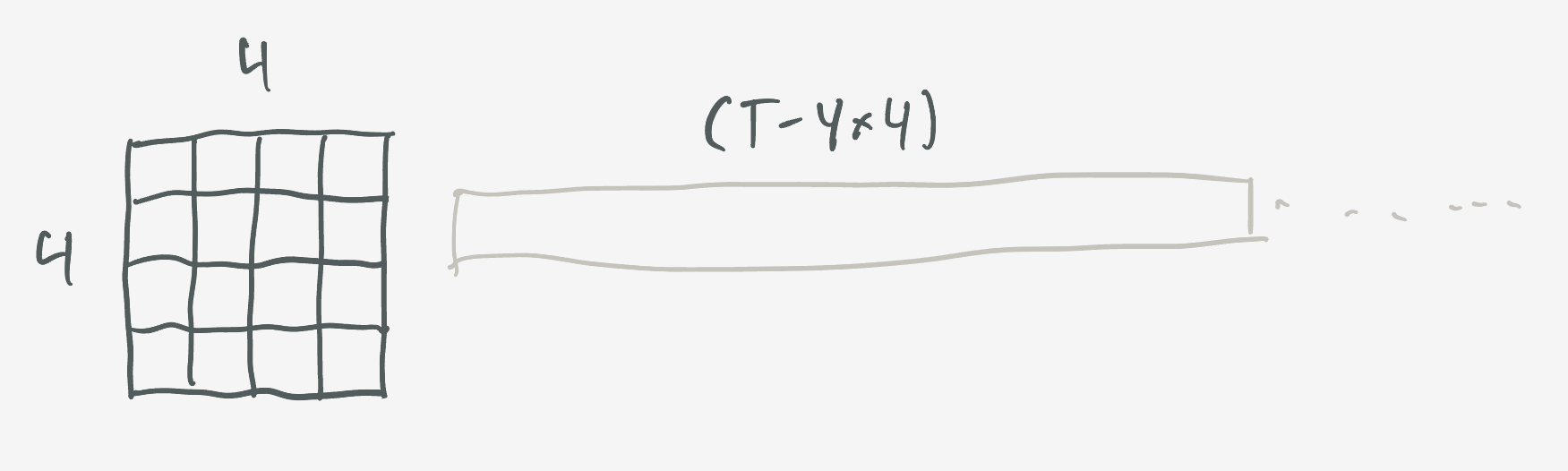
A valid Loteria board is then any shuffle of this setup.
With that in place we can count.
There are
- $4$ ways to place the rows, with $4$ ways to leave one out,
- $4$ ways to place the columns, with $4$ ways to leave one out,
- $9$ ways to place the squares, with $4$ ways to leave one out, and
- $1$ way to place the corners, with $4$ ways to leave one out,
There are also $T - (m-1) - 1)$ places to put the card that’s left out of the almost-winning pattern.
Generalizing, this makes $N(m) = (4 + m^2 + m^2 + 4(m-1)^2)\times(T-m)$ ways to be $1$ card from a win after the $4^\text{th}$ draw.
The total number of ways to place the $4$ cards without winning is the total number of ways to place $4$ cards out of $T$ total locations, less the number of ways to win in $4$ draws = $\binom{T}{4} - (1 + 2m + (m-1)^2).$
So, the probability of being one card placement away from a win after $4$ cards is
\[\begin{align} P(\text{poised to win after 4}) &= \dfrac{N(m)}{N_\text{total}(\text{no win})} \\ &= \dfrac{(4 + m^2 + m^2 + 4(m-1)^2)\times(T-m)}{\dbinom{T}{4} - (1 + 2m + (m-1)^2)} \end{align}\]The overall probability to win on the $5^\text{th}$ draw is the probability to be poised to win after the $4^\text{th}$ draw times the probability of correctly placing the $5^\text{th}$ card. As there is $1$ correct position and $(T-4)$ positions remaining, this is
\[P(\text{win on }5^\text{th}\rvert\text{no win by }4^\text{th}) = \dfrac{(4 + m^2 + m^2 + 4(m-1)^2)\times(T-m)}{\dbinom{T}{4} - (1 + 2m + (m-1)^2)}\frac{1}{T-4}\]The prediction for the case at hand is $P(\text{win on }5^\text{th}\rvert\text{no win by }4^\text{th}) = 8/35137 \approx 0.00022768022.$
Setting $m=4$ and varying $T,$ we can plot the prediction against an $N=10^6$-round simulation.
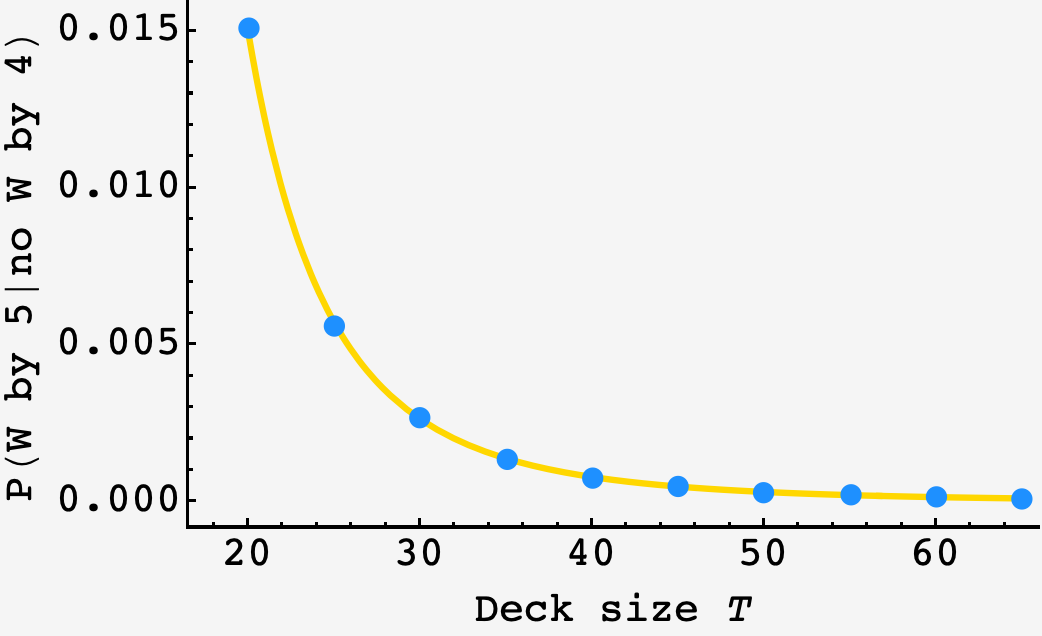
It looks pretty good.
Since each Loteria board is independent, the probability of a single winner on the $5^\text{th}$ draw is
\[1000 P(\text{win on }5^\text{th}\rvert\text{no win by }4^\text{th}) \left[1-P(\text{win on }5^\text{th}\rvert\text{no win by }4^\text{th})\right]^{999} \approx 0.181356\]