Question: an entrepreneur runs a time-share for goats. Each goat has their favorite floor, but it’s first come first served. If a goat arrives to find their favorite floor occupied, they’ll go up one floor at a time, looking for an empty one. If they don’t find one, then they’ll go to the party lounge on the penthouse floor. What is the probability the entrepreneur will not have to host a goat party?
Solution
Let’s call a good goat tower (GGT) a goat tower in which there is one goat to a floor with no goats on the penthouse. We’re going to find the probability of a GGT by counting the number of ways to form a good goat tower.
Counting
If we have a GGT, it means that the final goat arrived to find a floor $e$ open, and that their preferred floor was less than or equal to $e.$
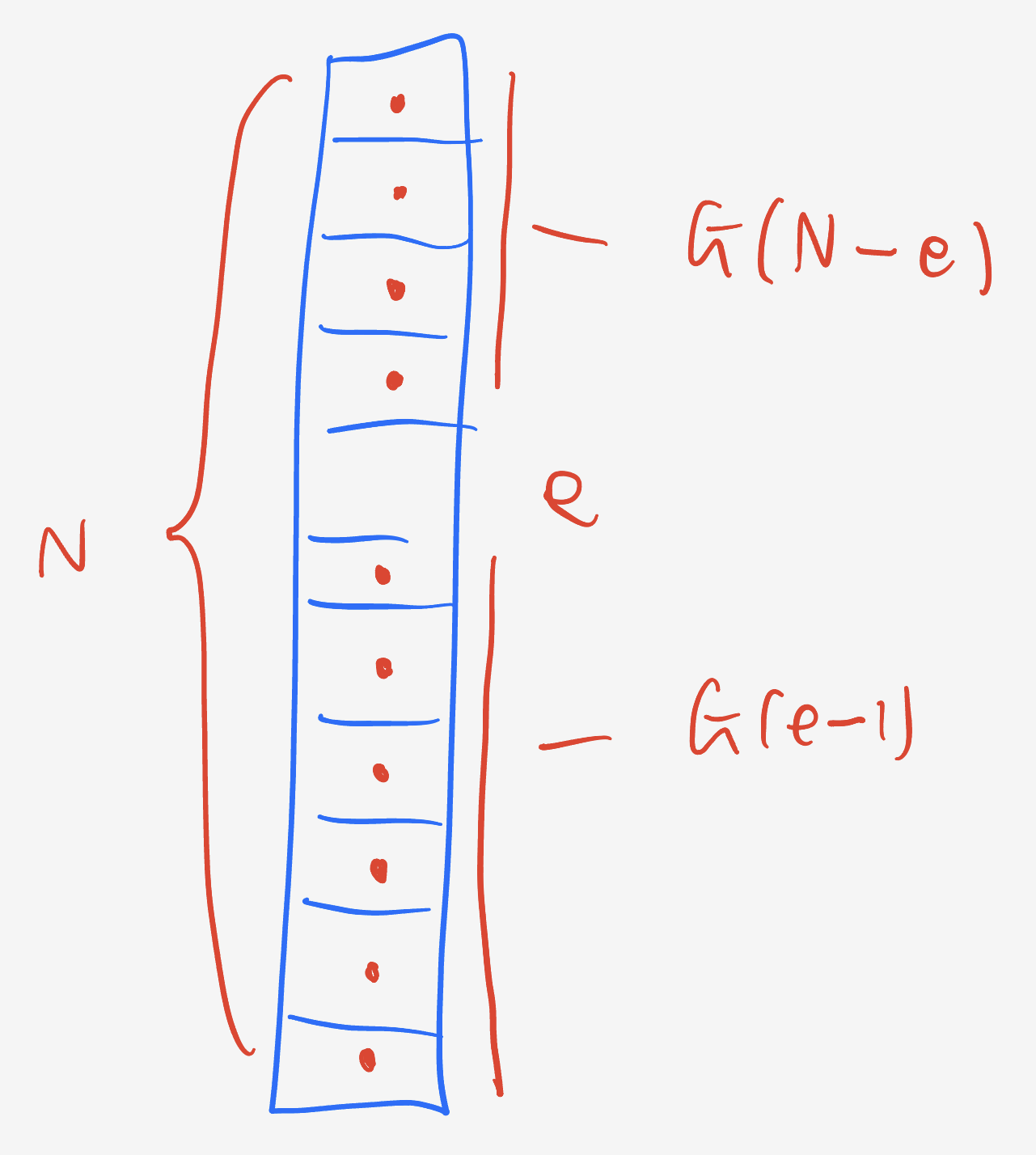
This also means that all the goats on floors $(e+1)$ through $N$ would form their own GGT, independent of the goats on floors $1$ through $(e-1)$ and likewise for the goats on floors $1$ through $(e-1).$
Finally, there are $\binom{N-1}{e-1}$ ways to divide the $(N-1)$ goats between the upper and lower GGTs.
Recursion
Putting it all together, there are $\binom{N-1}{e-1}\cdot e\cdot G(N-e)\cdot G(e-1)$ ways to form a GGT. The empty floor $e$ can be any floor from floor $1$ to $N,$ so
\[G(N) = \sum\limits_{e=1}^N \binom{N-1}{e-1} \cdot e \cdot G(N-e)\cdot G(e-1),\]with the base conditions $G(1) = G(0) = 1.$
Since there are $N^N$ possible preference lists for the goats, the probability of a GGT is $P(N) = G(N)/N^N.$
Evaluating, we get the initial values of $P(N):$
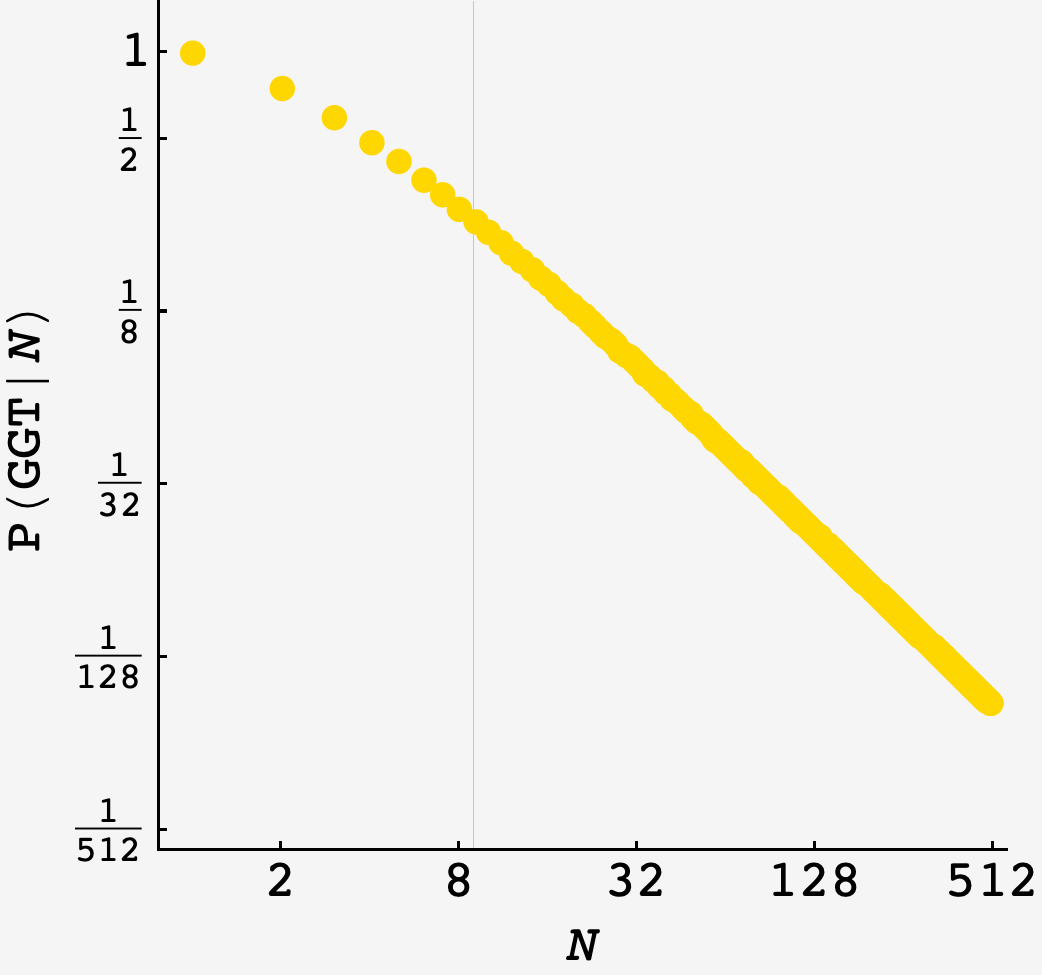
\[\begin{array}{c|c|c} N & P(N) \\ \hline 1 & 1 \\ 2 & \frac{3}{4} = 0.75 \\ 3 & \frac{16}{27} \approx 0.592593 \\ 4 & \frac{125}{256} \approx 0.488281 \\ 5 & \frac{1296}{3125} = 0.41472 \\ 6 & \frac{16807}{46656} \approx 0.360232 \\ 7 & \frac{262144}{823543} \approx 0.318312 \\ 8 & \frac{4782969}{16777216} \approx 0.285087 \\ 9 & \frac{100000000}{387420489} \approx 0.258117 \\ 10 & \frac{2357947691}{10000000000} \approx 0.235795 \\ 11 & \frac{61917364224}{285311670611} \approx 0.217017 \\ 12 & \frac{1792160394037}{8916100448256} \approx 0.201003 \end{array}\]Plotting, we can see that when the number of goats gets big, the probability of a GGT dies like \(\sim N^{-1}:\)