Question: one point is selected at random from each side of an equilateral triangle. What is the probability that the resulting triangle contains the center of the original?
Solution
We need to tally up the weight of all triplets of points $\{s_1, s_2, s_3\},$ (with each $s_i$ drawn from side $i$ of the equilateral triangle) that contain the center point $\mathbf{c} = \left(\frac12,\frac{\sqrt{3}}{6}\right).$
To fix an order, we’ll pick $s_1,$ then $s_2,$ and then $s_3$ (counterclockwise).
If we pick $s_1 \in \left(0,\frac12\right),$ then it will be on the same side of the middle as point $s_3.$ Otherwise, it will be on the same side as $s_2.$ These two cases are symmetric, so we can just do it once and double our result.
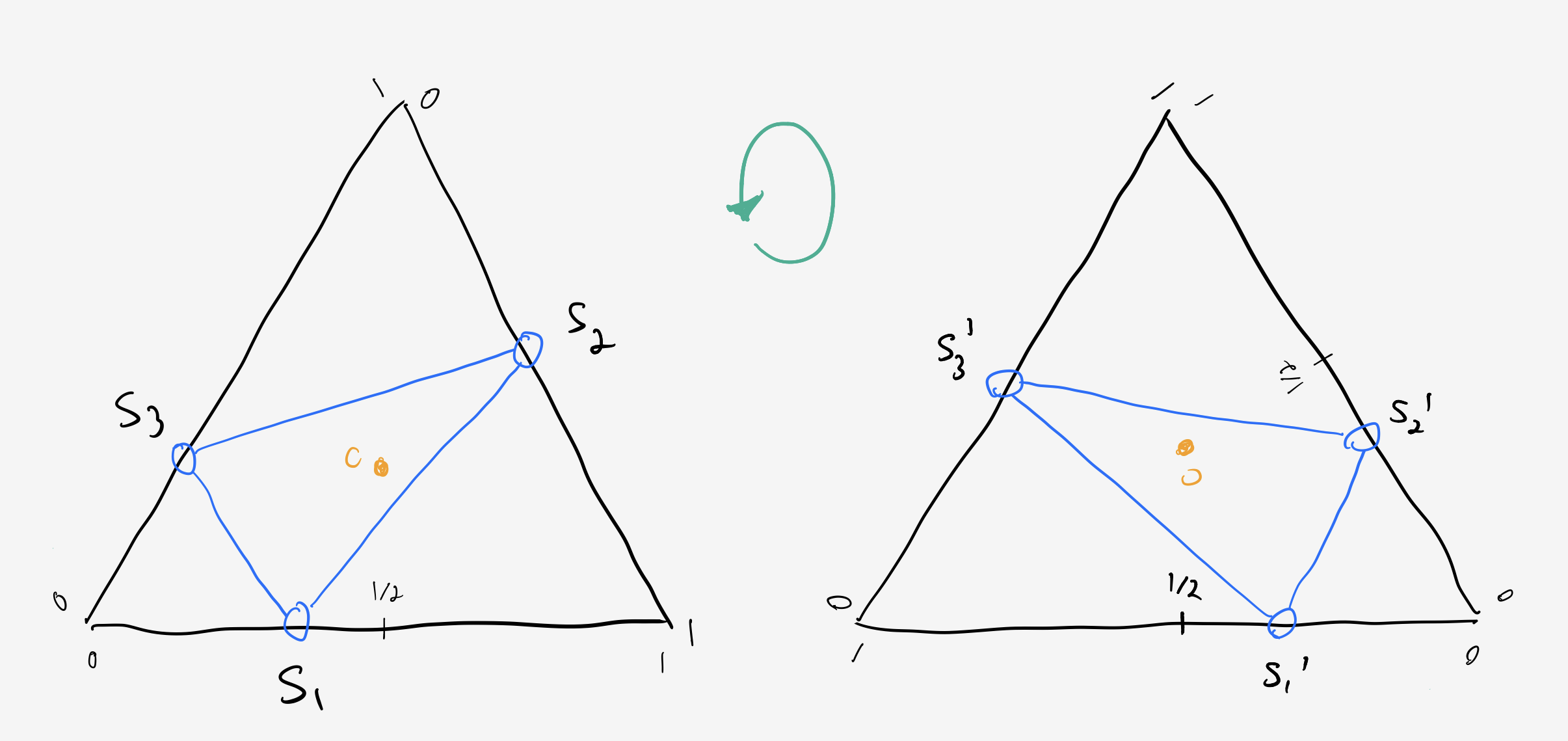
If the triangle were isosceles or scalene, we’d need to handle this case separately (but similarly).
Starting from point $s_1,$ we shoot at side 2, hitting at point $s_2,$ and from there bounce to $s_3.$ In order to contain the center, the shot has to pass under the center, the bounce has to pass over it, and the line of sight from $s_3$ to $s_1$ has to pass the center on the left.
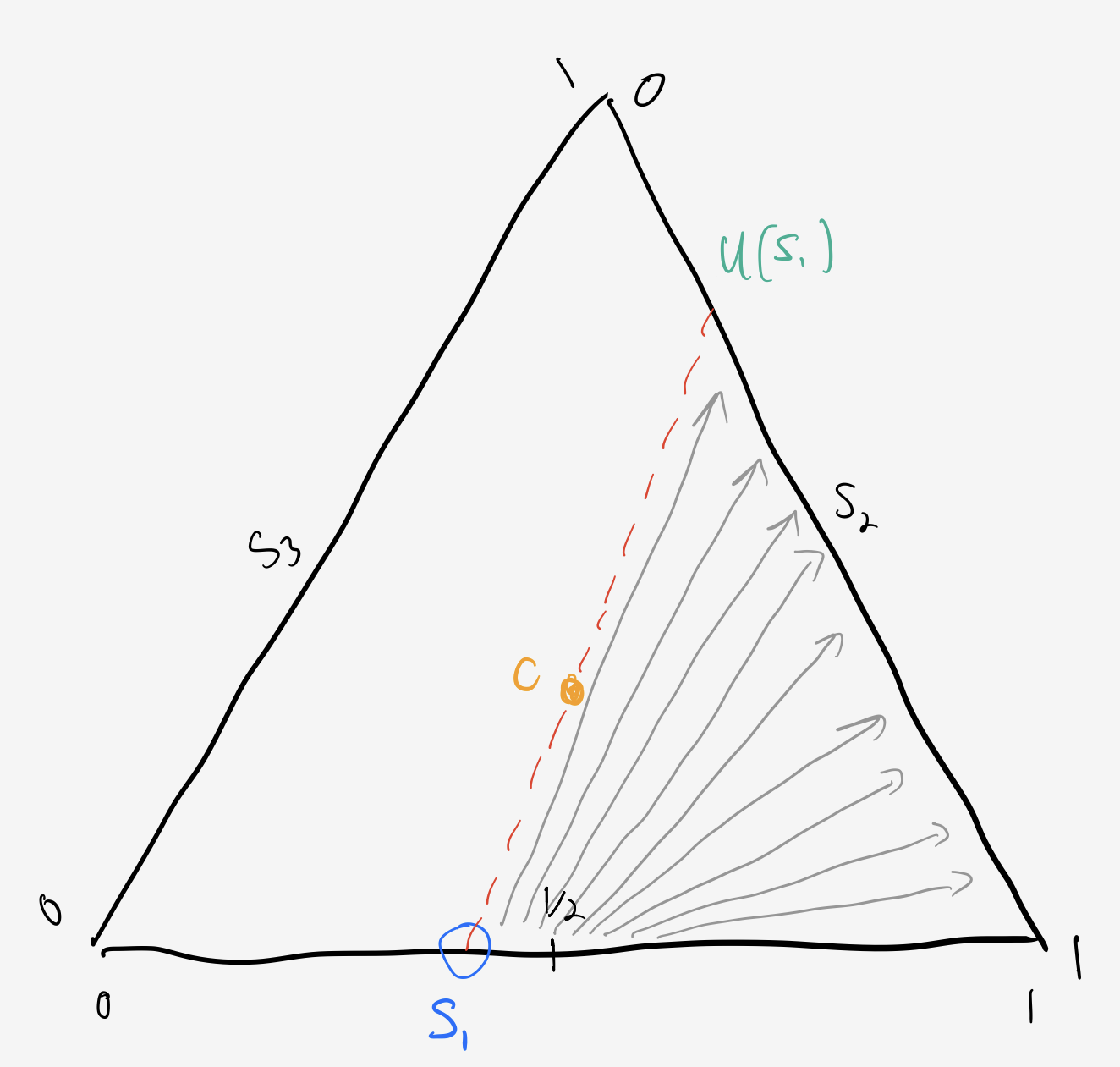
The shot
The shot can hit side 2 anywhere from the bottom right corner of the triangle up to the intersection of side 2 with the ray from $s_1$ through the center, which serves as an upper bound, $U(s_1).$
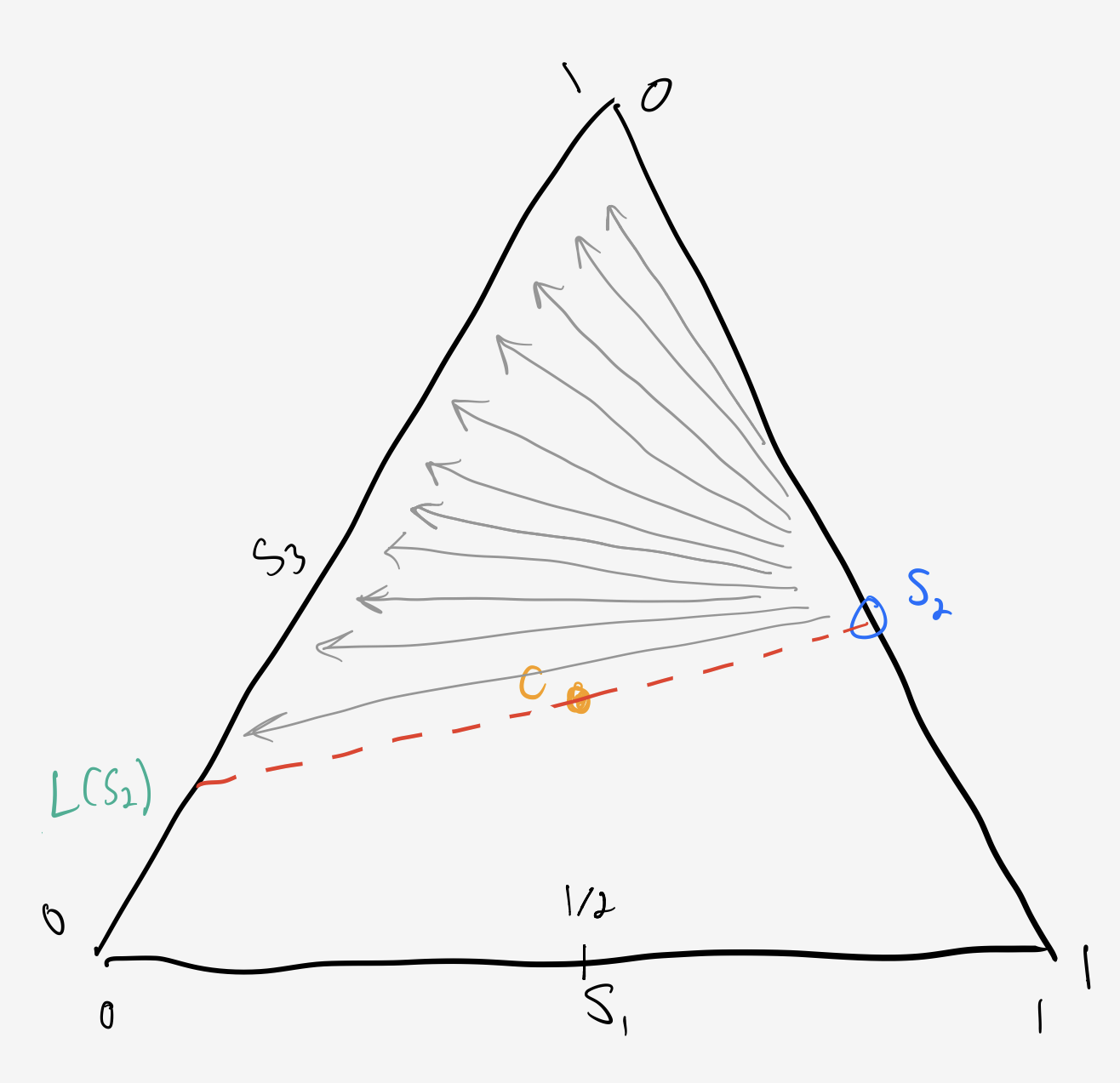
The bounce
If $s_2 > \frac12,$ then the bounce has a lower bound, $L(s_2),$ which we find by intersecting the ray from $s_2$ through the center with side 3. but if $s_2 < \frac12$ then the bounce can hit side 3 anywhere in $\left(0,1\right).$
Add ‘em up
So, we have to scatter the shot from $s_1$ to all permissible points on side 2, and then on to all permissible points in side 3. Again, if $s_2 < \frac12,$ then the bounce can scatter anywhere on side 3. At the end, we sum over all values of $s_1.$
Putting it all together, the total weight of the permissible triples is
\[2\left(\int\limits_{0}^{\frac12}ds_1 \int\limits_{U(s_1)}^{\frac12} ds_2 + \int\limits_{0}^{\frac12}ds_1 \int\limits_{\frac12}^1 ds_2 \int\limits_{L(s_2)}^1 ds_3\right).\]All that’s left is to compute the bounds $U(s_1)$ and $L(s_2).$
$U(s_1)$ and $L(s_2)$
The ray from $s_1$ through the center is
\[\left(s_1, 0\right) + \left[\mathbf{c} - \left(s_1, 0\right)\right]t,\]while side two is
\[\frac12\left(1, \sqrt{3}\right) + \left[\left(1,0\right) - \frac12\left(1, \sqrt{3}\right)\right]s_2.\]Setting these two expressions equal and solving for $s_2$ gets $U(s_1) = (1-2s_1)/(1-3s_1).$
Likewise, setting up the ray for the bounce and intersecting it with side 3 gets $L(s_2) = (1 - 2s_2)/(2 - 3s_2).$
The sum total
Making the replacements, and evaluating the integral we get
\[\begin{align} P(\mathbf{c} \in \triangle s_1s_2s_3) &= \displaystyle 2\left(\int\limits_{0}^{\frac12}ds_1~\int\limits_{\frac{1-2s_1}{2-3s_1}}^{\frac12} ds_2 + \int\limits_{0}^{\frac12}ds_1~\int\limits_{\frac12}^1 ds_2~\int\limits_{\frac{1 - 2s_2}{1 - 3s_2}}^1 ds_3\right) \\ &= \frac23 \log 2 \\ &\approx 0.4621\ldots \end{align}\]