Question: Suppose you have a chain with infinitely many flat (i.e., one-dimensional) links. The first link has length $1,$ and the length of each successive link is a fraction $f$ of the previous link’s length. As you might expect, $f$ is less than $1.$ You place the chain flat on a table and some ink at the very end of the chain (i.e., the end with the infinitesimal links).
Initially, the chain forms a straight line segment, and the longest link is fixed in place. From there, the links are constrained to move in a very specific way: The angle between each chain and the next, smaller link is always the same throughout the chain. For example, if the $N^\text{th}$ link and the $N+1^\text{st}$ link form a $40$ degree clockwise angle, then so do the $N+1^\text{st}$ link and the $N+2^\text{nd}$ link.
After you move the chain around as much as you can, what shape is drawn by the ink that was at the tail end of the chain?
Solution
The chain is made of a bunch of links of lengths $1, f, f^2, \ldots $
We can write down the position of each endpoint in terms of the last. take a chain with two links, with endpoints $\mathbf{p}_0,$ $\mathbf{p}_1,$ and $\mathbf{p}_2.$
To find $\mathbf{p}_1,$ we start at $\mathbf{p}_0,$ lay down a link of length $1$ and rotate it $\phi$ degrees:
\[\mathbf{p}_1 = \mathbf{p}_0 + \mathbf{R}_\phi\cdot \mathbf{1}.\]Finding $\mathbf{p}_2$ is almost the same, we start at $\mathbf{p}_1,$ lay down a link of length $f$ and rotate it by $2\phi$ degrees:
\[\mathbf{p}_2 = \mathbf{p}_1 + \mathbf{R}_\phi^2\cdot \left(f\mathbf{1}\right).\]Recursing, $\mathbf{p}_2$ is just
\[\begin{align} \mathbf{p}_2 &= \mathbf{p}_0 + \mathbf{R}_\phi\cdot\mathbf{1} + f\mathbf{R}_\phi^2\cdot\mathbf{1} \\ &= \mathbf{R}_\phi\cdot\mathbf{1} + f\mathbf{R}_\phi^2\cdot\mathbf{1} \\ &= \frac{1}{f}\left[f\mathbf{R}_\phi + f^2\mathbf{R}_\phi^2\right]\cdot\mathbf{1} \end{align}\]This pattern carries on, and the $n^\text{th}$ link is
\[\mathbf{p}_n = \frac{1}{f}\left[f\mathbf{R}_\phi + \left(f\mathbf{R}_\phi\right)^2 + \ldots + \left(f\mathbf{R}_\phi\right)^n\right]\cdot\mathbf{1}.\]We can put this in a more compact form that makes the behavior clearer. If we act on $\mathbf{p}_n$ with $f\mathbf{R}_\phi$ and subtract it from $\mathbf{p}_n,$ we get:
\[\mathbf{p}_n = \overbrace{\frac{f\mathbf{R}_\phi}{1 - f\mathbf{R}_\phi}}^\text{$n$-independent}\times\overbrace{\left(1-\left(f\mathbf{R}_\phi\right)^n\right)}^\text{$n$-dependent}\cdot\mathbf{1}\]The first term describes the prevailing twist of the chain and generates smooth global motion, and the second term is an adjustment that accounts for the relative movement of individual links and produces interesting twiddly-dees and doo-dahs for early endpoints in the chain.
For large values of $n,$ the second term oscillates around a central point, which is where the end of the chain lives. Since $f < 1,$ this orbit closes and, for large $n,$ the motion is provided by the first term alone.
Concrete
Up to here we haven’t picked a representation for the rotation $\mathbf{R}_\phi$ and the arrow $\mathbf{1}.$ Since the chain breaks down to rotations of the unit arrow, we’re going to use complex numbers.
In this picture, $\mathbf{R}_\phi = e^{i\phi}$ and $\mathbf{1} = e^{i0} = 1 + 0i.$
With this, we get
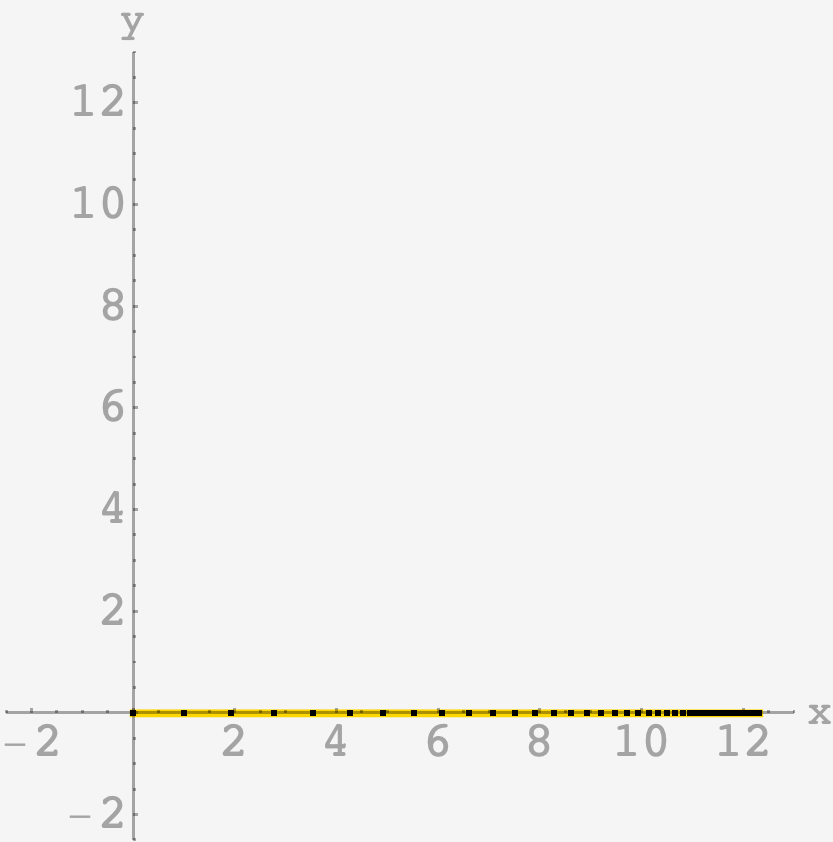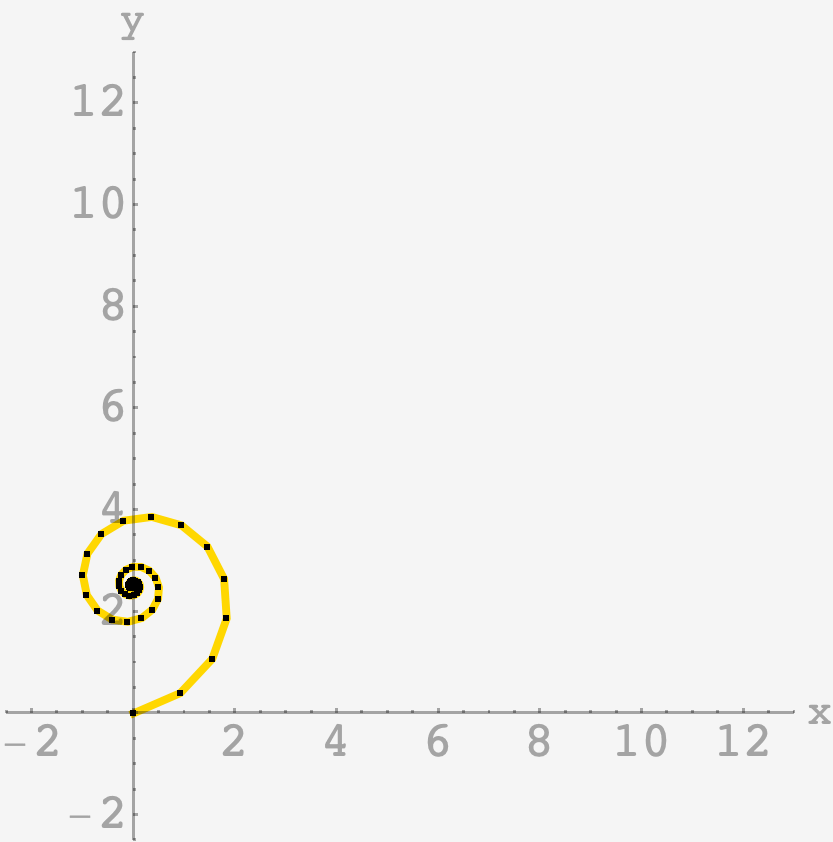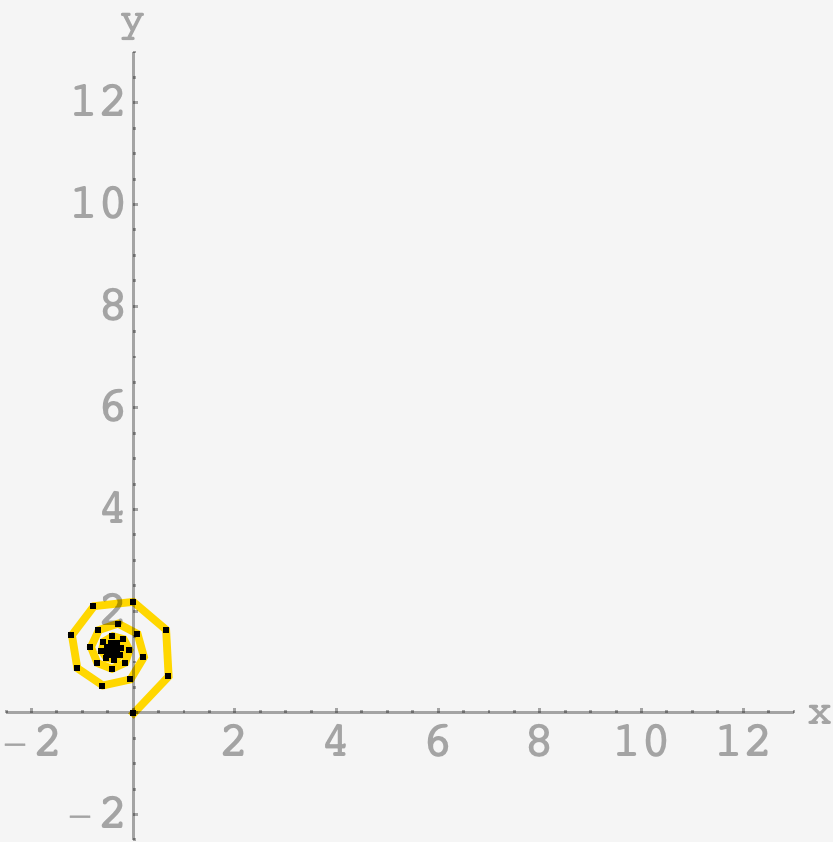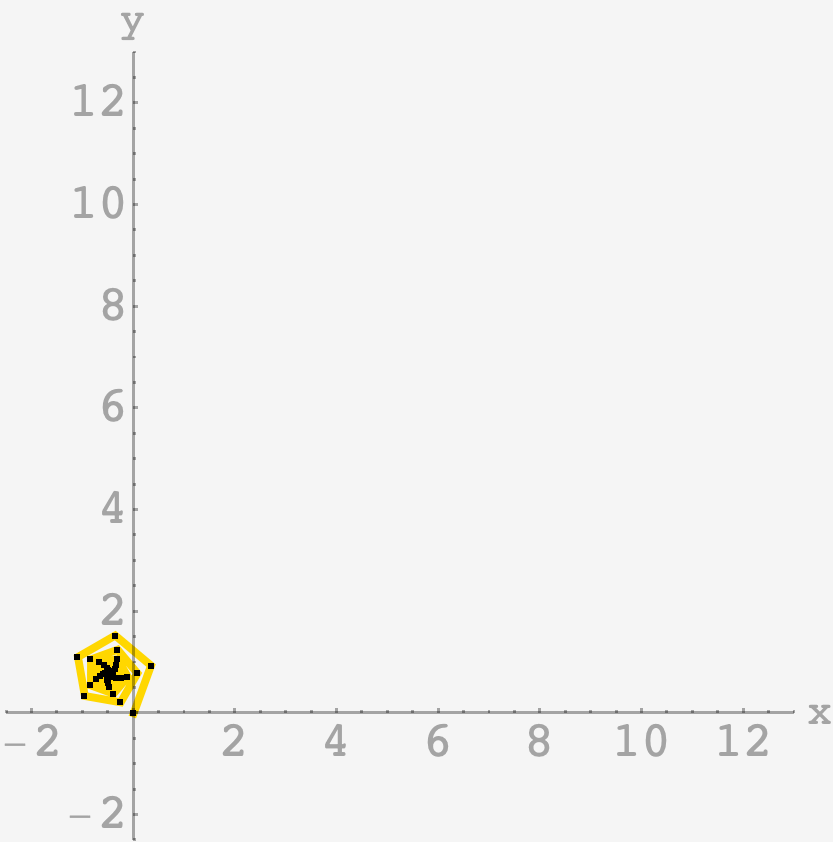
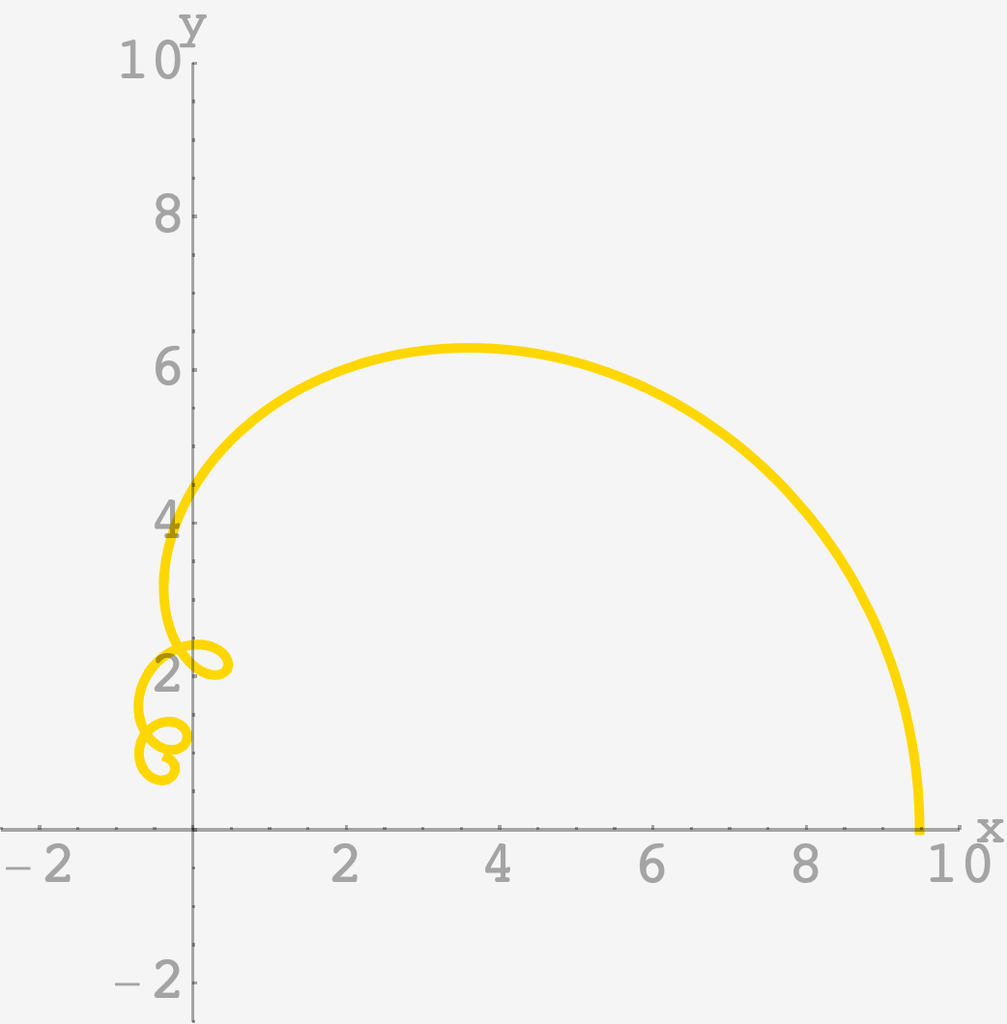
\[\mathbf{p}_n = \frac{e^{i\phi}}{1-fe^{i\phi}}\left[1-\left(fe^{i\phi}\right)^n\right]\]and we can plot the chain:
Focusing on one of the early endpoints, we see nice twiddly-dees and doo-dahs, as predicted:
The ink at the end of the chain
In the limit $n\rightarrow \infty,$ $\mathbf{p}_n$ becomes
\[\mathbf{p}_n = \frac{e^{i\phi}}{1-fe^{i\phi}}\]Bringing everything to the surface, we have
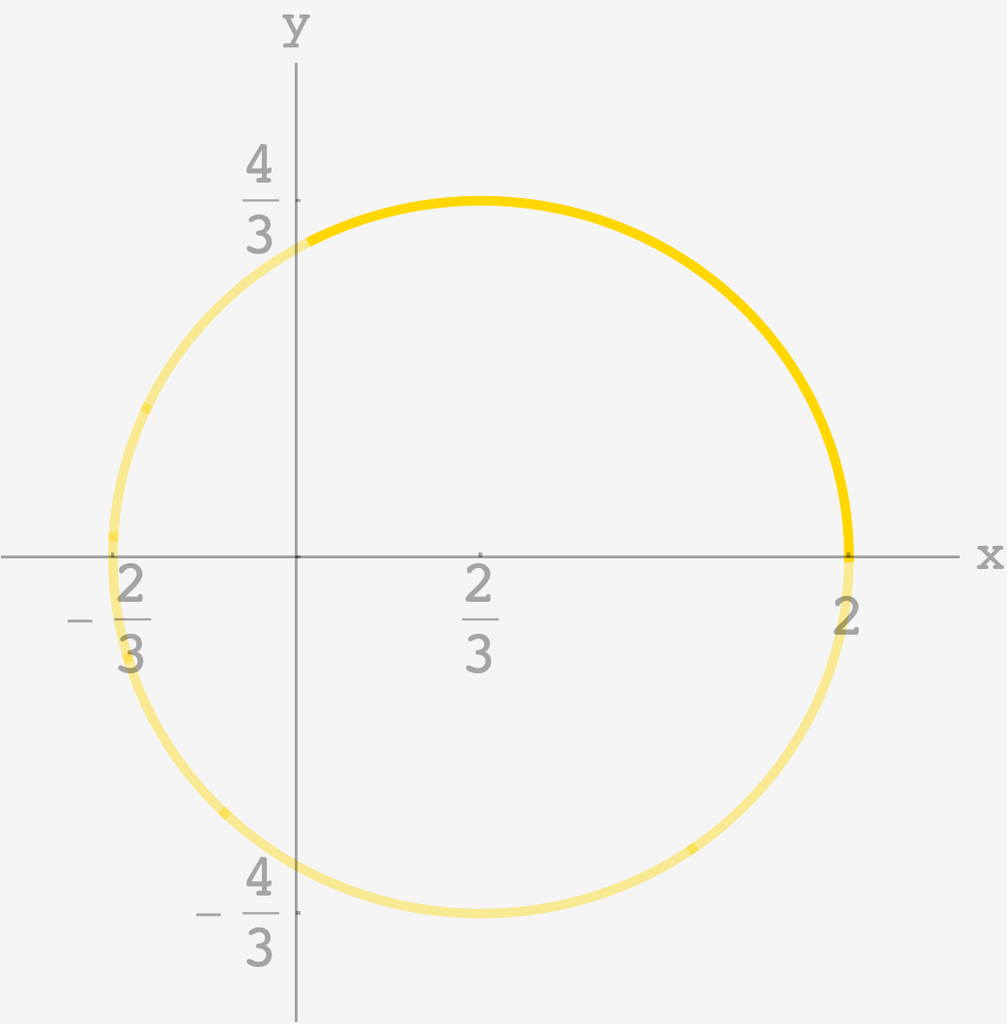
\[\begin{align} \mathbf{p}_n &= \frac{e^{i\phi}}{1-fe^{i\phi}}\frac{1-fe^{-i\phi}}{1-fe^{-i\phi}} \\ &= \frac{e^{i\phi} - f}{1 + f^2 - f(e^{i\phi} + e^{-i\phi})} \\ &= \frac{(\cos\phi - f) + i\sin\phi}{1 + f^2 - 2f\cos\phi} \end{align}\]which is a circle of radius $(1-f^2)^{-1}$ centered on the point $f(1-f^2)^{-1} + 0i$ as, e.g., the distance formula confirms.
The path of $\mathbf{p}_\infty$ for $f = 0.5$ and $\phi = 40\,^\circ.$