The Battle of Los Angeles

Question: It’s the day after the championship parade and you are Lebron James. Doc Rivers has been deposed, Paul George’s name is on the trade winds, and Patrick Beverley hasn’t thought about trash talk in over a month. Needless to say, life is good. But one day, your brother in arms, The Brow, Anthony Davis himself, challenges you to some $1$ on $1,$ first to score wins! Due to his dominant height and wingspan, he’s able to grab every single rebound, even the ones off his own three pointers! “What’s a king to do?”, you wonder. But then you realize — your career steal line is a full $0.2$ steals per game higher than Davis’. Every possession, you have the chance to steal the ball away with probability $L_\text{steal}.$ If yours and Anthony’s shot percentages are $L_\text{score}$ and $D_\text{score},$ respectively, then what is the chance that you, Lebron James, win the $1$ on $1$ game? Inversely, how high does your steal probability, $L_\text{steal},$ need to be for it to be an even match?

(FiveThirtyEight)

Solution

On first glance, Davis has a pretty nice advantage since he takes possession of the ball after every missed three point shot. However, Lebron has a chance to steal every time Davis takes possession. If Lebron was barred from stealing in the case where Davis starts the game with the ball, then the 1:1 would be perfectly symmetric if the probability $L_\text{steal}$ was $1/2.$ Since Lebron can steal in the first possession, we should expect the $L_\text{steal}$ required for a fair game to be something less than $1/2.$

Half-court pinball

To start, it’s good to get a handle on the kinds of games we can expect.

Lebron could start with the ball, shoot and miss, steal it from Davis, shoot and miss again, before Davis shoots and misses, before Lebron fails to steal the ball, before Davis shoots and scores. Just as easily, Davis could take the first possession, Lebron could fail to steal, and then Davis could score on his first shot attempt. There are $7$ steps in the first version and $3$ in the second, and there infinitely many other cases to consider, some of which are infinitely long.

Sample trajectory where the game starts ($\mathbf{S}$) with Davis winning the coin flip (ball to $\mathbf{D}$), followed by Davis missing a shot (ball back to $\mathbf{D}$), followed by Lebron stealing the ball (ball to $\mathbf{L}$), followed by Lebron scoring (game ends at $\mathbf{LS}$).

Despite the variety, we can consider the possibilities in three main steps. The first is from the beginning of the game $\mathbf{S},$ the second is Lebron possessing the ball $\mathbf{L}$ and the third is Lebron scoring $\mathbf{LS}.$ In the first and second steps, the ball can spend time with Davis ($\mathbf{D}$) before going back to Lebron.

From the top, Lebron can start with the ball (probability $1/2$), or it can go to Davis (probability $1/2$) who shoots and misses $0$ or more times before Lebron steals it (probabiliy $L_\text{steal}$). If Davis shoots it and misses, it means that Lebron failed to steal it, so the probability for Davis to miss a shot is $\left(1-L_\text{steal}\right)D_\text{miss}.$

Since the steps

return to the same state (Davis possessing the ball), they can form loops of arbitrary length, and the total probability that Lebron comes into possession of the ball is

which has a geometric series in $\left(1-L_\text{steal}\right)D_\text{miss},$ and is equal to

Once Lebron takes possession, the possibilities get more intricate. But a shift in perspective makes it manageable.

Diagrammatics

In the first step, we discovered a geometric series hiding out in the possible ways that Davis can possess the ball without scoring. But that’s because we started by enumerating possibilities. If we think about the structure of things, we can generate the infinite possibilities by design.

Above, the terms $\left(1-L_\text{steal}\right)$ and $D_\text{miss}$ always appear, together, $0$ or more times in a row, and they’re always followed by a Lebron steal on the right. Seeing this, we can think of $\left(1-L_\text{steal}\right)D_\text{miss}$ as a repeatable block:

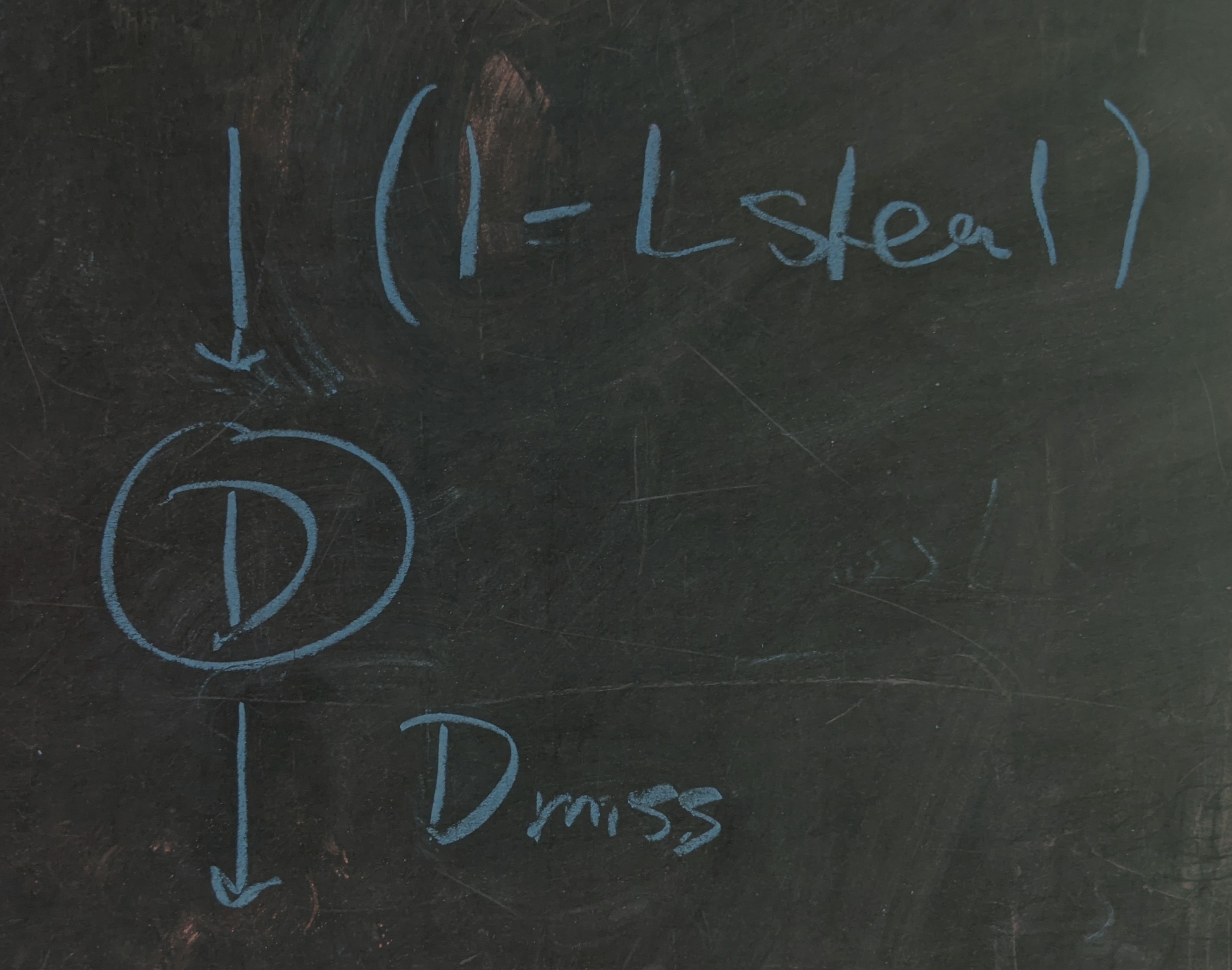
For Davis to have a shot attempt means that Lebron failed to steal the ball (probability $\left(1-L_\text{steal}\right)$), followed by the missed shot from Davis (probability $D_\text{miss}$).

The entire set of possibilities for Davis doing things with the ball before Lebron takes possession is one element from the set of looped units, followed by a steal from Lebron, represented as

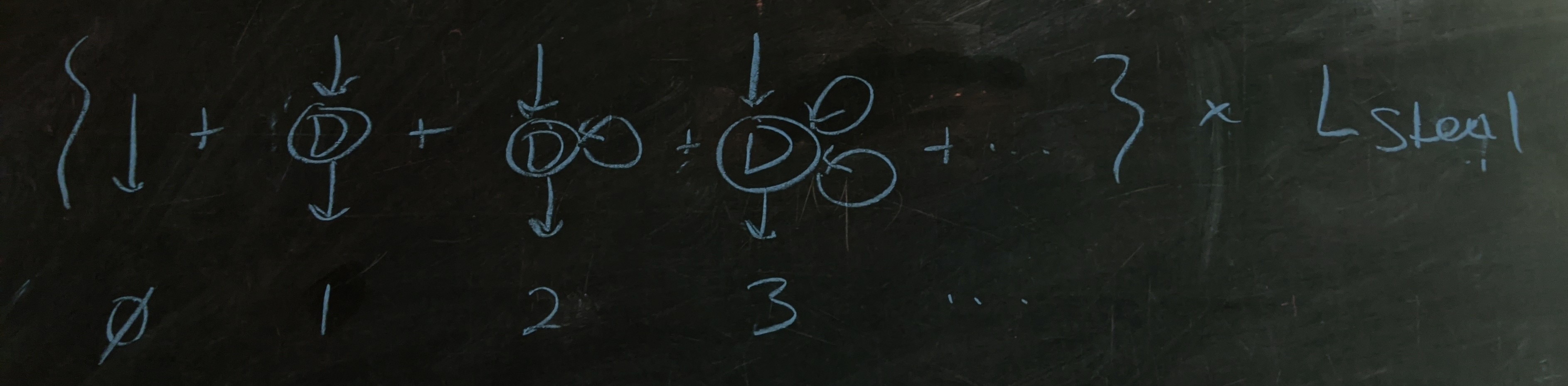
or, in symbols:

Second stage

In the second stage, we are waiting for Lebron to make a shot. Before that happens, Lebron can miss a shot before Davis misses one or more shots before Lebron steals the ball back from Davis.

But once the ball is back to Lebron, he can miss another shot and embark on another excursion into Davis possessions. It helps if we think at this second layer of abstraction first. Lebron can miss a shot, followed by Davis doing something, followed by Lebron stealing it back. And he can do this a potentially infinite number of times before taking a shot and making it.

This makes a block

To account for the fact that this step can loop an infinite number of times, we have

But $\text{Davis does something}$ accounts for an infinite number of possibilities itself, which we found above, so the total probability of all the things the ball can do before Lebron scores is equal to

Putting it all together

The last step is for Lebron to actualy score, which happens with probability $L_\text{score}$ when Lebron has possession of the ball. So, the probability that Lebron wins the game is

As a quick test, we can check the case where $L_\text{steal} = 0$ and $L_\text{steal}=1.$ When Lebron and Davis have identical shooting percentages of $1/2$, this yields $P_\text{Lebron}=1/4$ and $P_\text{Lebron}=1,$ which makes sense. If Lebron can’t steal, his only chance is to win the coin flip and make his shot, $1/2\times 1/2$ and if he can always steal, then Davis can’t shoot, so Lebron always wins.

If we plug in $D_\text{miss} = L_\text{miss} = 1/2,$ we can see how $P_\text{Lebron}$ varies as a function of $L_\text{steal}$ in the standard problem. Doing so, the expression for $P_\text{Lebron}$ collapses to

But our solution can handle the problem, whatever their individual shooting percentages.

Finding $L_\text{steal}$

We can solve the equation above for $L_\text{steal}$ so that we can find the required steal probability needed as a function of Lebron’s desired winning percentage:

Plugging in $L_\text{score} = D_\text{score} = P_\text{Lebron} = 1/2$ shows that we need $\boxed{L_\text{steal} = 1/3}$ for Lebron to have a $50\%$ chance to win.

$1$ on $1$ multiverse

Using the general result can explore the outcome for any combination of shot percentages for Lebron and Davis as a function of the steal probability $L_\text{steal}.$ Even when Lebron’s shot percentage gets very low ($\approx 5\%$), he can still manage to win as long as $L_\text{steal}$ is high enough, though it has to be $\gtrsim 80\%$ before he has a reasonable chance.

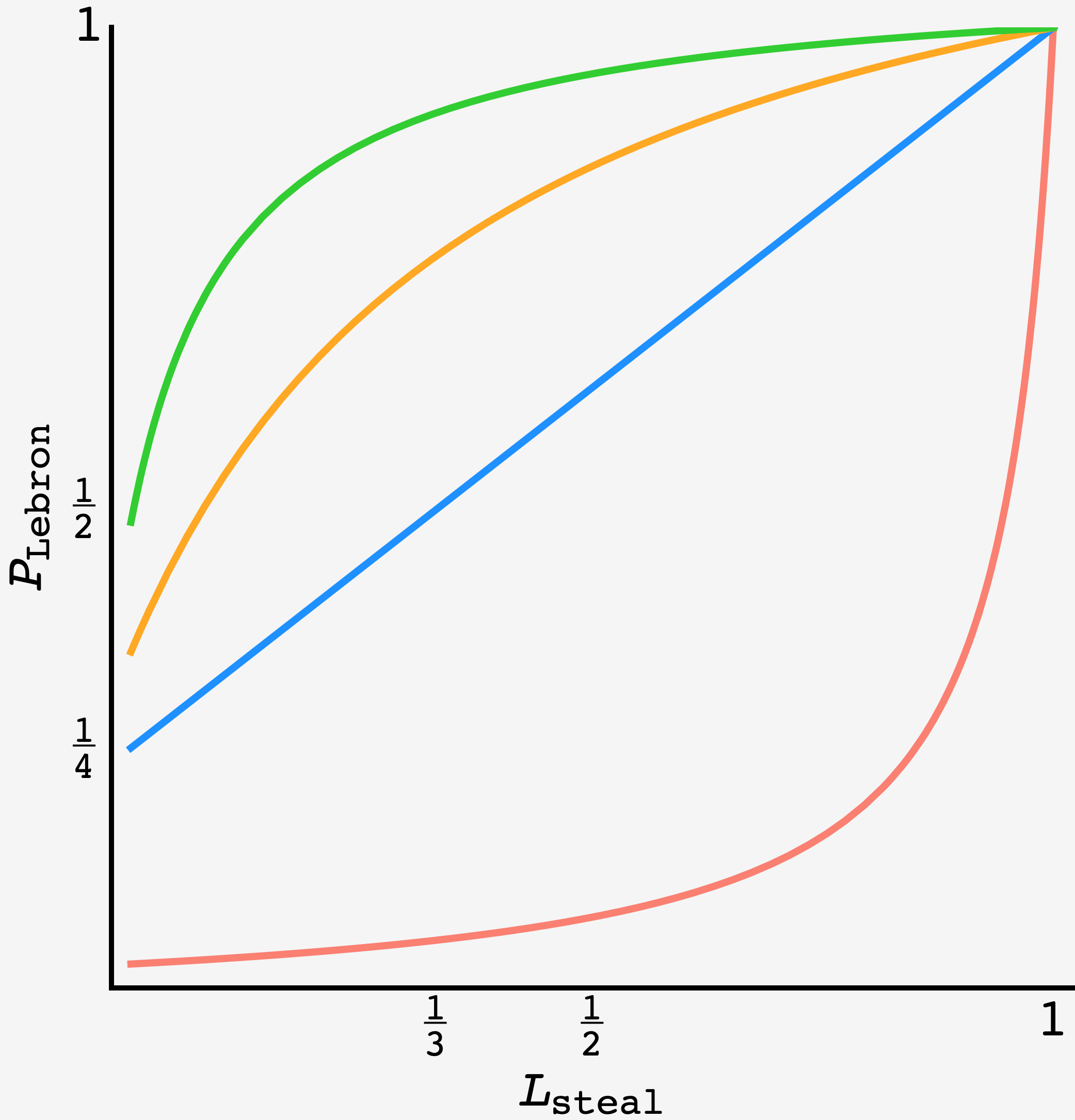
$P_\text{Lebron}$ vs. $L_\text{steal}$ for various values of $\left(L_\text{score},D_\text{score}\right).$ The curves are plotted for $\color{red}{\left(L_\text{score}=0.05,D_\text{score}=0.95\right)},$ $\color{blue}{\left(L_\text{score}=0.5,D_\text{score}=0.5\right)}$ $\color{orange}{\left(L_\text{score}=0.7,D_\text{score}=0.2\right)},$ and $\color{green}{\left(L_\text{score}=0.97,D_\text{score}=0.1\right)}.$